不同阻尼体系的运动状态判别法研究

黎 莹， 张之颖， 魏洪杨

(1. 西安交通大学 城市学院，西安 710018；2. 西安交通大学 人居环境与建筑工程学院，西安 710049)

在多自由度体系动力分析中，根据体系整体耗能模式的不同，可以分为经典阻尼体系与非经典阻尼体系[1]。经典阻尼体系[2]具有协调一致的耗能特性，振动过程中体系各点的运动状态保持连续一致，运动方程可采用振型叠加等算法进行分析，其动力问题不仅求解简单，而且具有明确的物理意义；而非经典阻尼体系[3]，体系内部运动状态难成连续一致，其正则主模态空间中运动方程耦合，没有传统概念上的所谓“振型”，运动方程无法采用振型叠加法求解，动力分析过程往往比较复杂或存在一定难度。

阻尼体系类别判断是结构动力分析方法择取的基础，阻尼体系性质不同，动力分析方法存在很大差异，计算结果也会出现较大出入。但迄今为止，关于阻尼体系的判定，缺乏明确的工程界定标准，其判定方法十分粗浅，致使动力分析方法的择取亦十分模糊。目前针对工程阻尼体系的判断，多以体系材料阻尼特性为判断基础，一般将阻尼特性均匀一致的体系判断为经典阻尼体系；而由多种材料组成的体系，如土-结构相互作用体系[4-6]、钢-混凝土组合结构体系[7]等，常被认为是非经典阻尼体系。然这种建立在材性上的粗浅判定方法，与实际现象并不完全相符，如复合材料领域中的共固化复合材料结构[8]，是典型的由多种材料组成的结构体系，工程实践表明，在结合性能完好条件下，按经典阻尼体系的动力分析结果，将与实验结果能够较好吻合；又如软土地基上的土-结构相互作用(Soil-Structure Interaction，SSI)体系，虽其组成部分的材性差别较大，但同济大学的振动台实测结果并没有反映出十分明显的非经典阻尼特性[9]。这说明，以材性为依据的阻尼体系的粗浅认知观点与工程实际存在着出入，这种仅建立在材性上的粗浅判定方法缺乏深入实际的基础性研究，也启示着开展阻尼体系判别方法的实质性基础研究的必要性。

1 不同阻尼体系的运动状态研究

经典、非经典阻尼体系的差异与其运动状态存在着直接关系，运动状态是阻尼体系最基础的表达方式。为了深入研究阻尼体系的基本界定方法，本文以相应的动力分析方法为切入点，来讨论不同阻尼体系运动状态上的差别。

所谓“运动状态”，是用于描述动力系统各点的位移、速度与加速度随时间的变化轨则，也可看作以一组流形的几何空间坐标来描述未来状态如何随当前状态的变化。

在状态空间表达方法中，一点的运动状态是以速度与位移为坐标进行描述，一点的运动状态连续，即要求该点的位移和速度连续，表现为该点的加速度存在。其加速度可表示为

(1)

由式(1)知，若一点加速度存在，则不仅要求其速度存在，即该点的位移-时间函数曲线须光滑连续，而且速度关于位移的导数存在，即其该点的速度-位移函数曲线也须光滑连续。

同理，若一个体系的运动状态连续，则在任意时刻，该体系各点速度存在，且各点速度函数关于自身位置坐标光滑连续。

常用黏滞阻尼模型下，一个体系的运动可由动力学方程描述为

[K]{u(x,t)}={p(x,t)}

(2)

对于式(2)的运动求解来说，采用经典与非经典阻尼体系动力分析方法的主要差异，关键在于其动力学方程能否解耦。若运动方程可以解耦，则其运动可由若干阶解耦模态的线性组合表示。而任意一阶解耦模态，是按体系有唯一挠曲形状的假定所求得。若令该模态下的挠曲线为形状函数，模态运动的基准点运动用广义坐标表示，则其任意一阶的解耦模态运动可由形状函数和广义坐标表达为

(3)

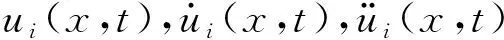
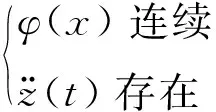
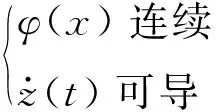
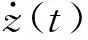
当运动呈现非经典阻尼体系时，由上推论可得，体系运动状态将出现下列任意一项：

(1) 任意时刻，体系的模态形状函数关于x不连续；

(2) 体系中存在一点的模态速度函数曲线关于时间t不光滑或不连续。

2 阻尼体系判别的工程实例

工程中多样化的结构体系，在不同动力作用下的运动状态往往并不相同，要判别动力作用下各类结构的阻尼体系类型，可具体分析其运动状态。

下面以三个工程实例来讨论体系运动状态连续性与阻尼体系之间的关系。

2.1 黏滑运动现象

工程中广泛存在黏滑运动现象，黏滑运动是指，在一定条件下，体系内部的两接触面出现相对静止或滑动两种运动状态[10]。如图1所示的具有滑移隔震系统的结构，在地震作用下的运动形式也可简化为该种类型。当滑移隔震支座发挥作用时，体系为非经典阻尼体系。本文从运动状态来分析出现这类现象的阻尼体系。

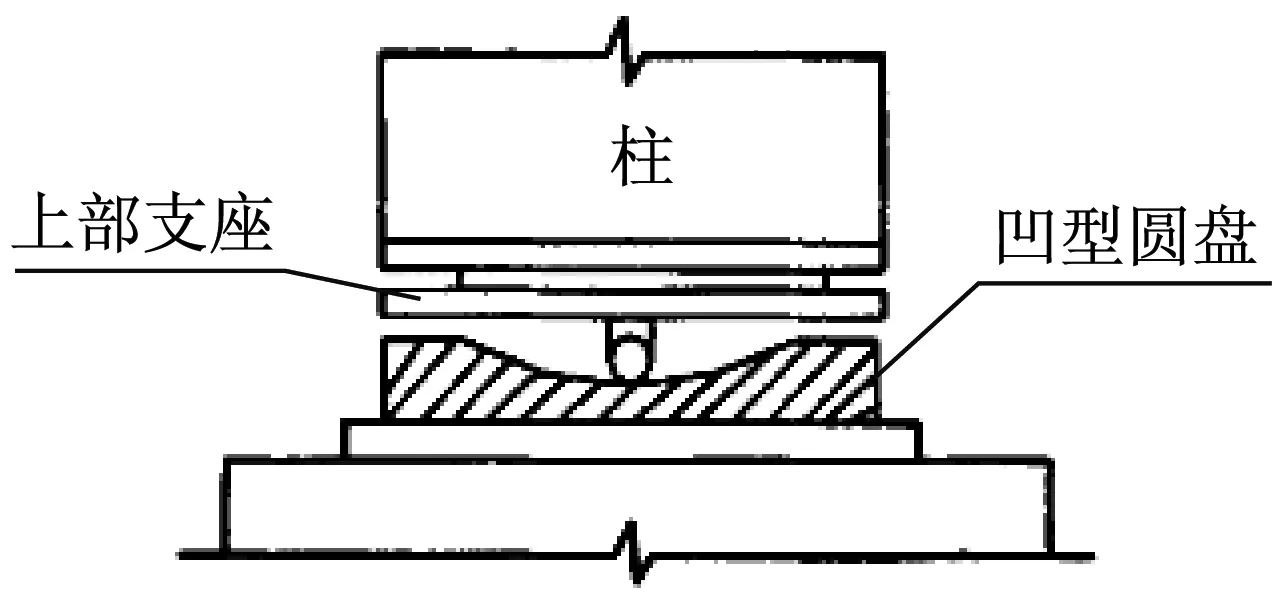
图1 摩擦滑移支座隔震系统

动力作用下，由于两部分各自的运动状态具有经典阻尼体系特性，即各自运动均可由相应的形状函数和广义坐标表示。取m1底部为坐标原点来考察体系的阻尼特性，设两部分第i阶形状函数分别为φ1i(x),(x∈(0,l1))和φ2i(x),(x∈(l1,l1+l2))，t时刻m1和m2的广义坐标分别为z1i(t)及z2i(t)，则两者的模态位移可以分别表达为

u1i(x,t)=φ1i(x)z1i(t)

(4)

u2i(x,t)=φ2i(x)z2i(t)

(5)

式中：u1i(x,t)，u2i(x,t)分别为m1,m2两部分t时刻的第i阶模态位移。

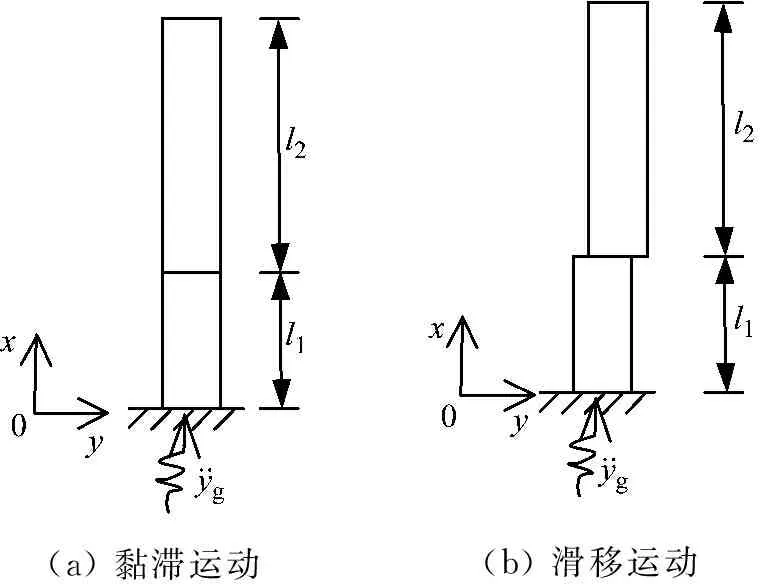
(a) 黏滞运动(b) 滑移运动

图2 体系黏滑运动示意图

Fig.2 Schematic diagram of stick-slip motion

(1)当黏滞运动时，如图2(a)，体系在交界面上运动连续，即任意t时刻，两者交界面处的第i阶模态位移、速度和加速度相等，即

(6)

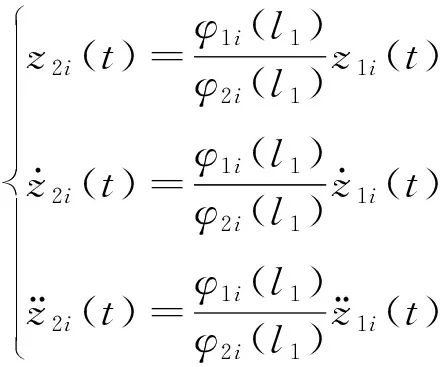
(7)

令

(8)

有

z2i(t)=Ψiz1i(t)

(9)

整个体系第i阶模态位移可以表达为

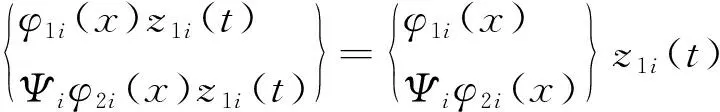
(10)

令

(11)

式中：φi(x)为分段函数。由式(8)知

φi(l1)=Ψiφ2i(l1)

(12)

由于该函数在分界点处连续，则体系的第i阶模态运动可表达为

(13)

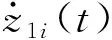
(2)当体系在交界面上出现滑移时，如图2(b)，即运动位移在交界面上不连续，虽其两部分各自仍可假设具有经典阻尼特性，各自模态位移仍可由式(4)、式(5)表达，但由于滑移存在，两者位移在界面处不连续，交界处必有模态位移差存在，设交界处某阶模态位移差为Δi(t)，则

φ1i(l1)z1i(t)=φ2i(l1)z2i(t)+Δi(t)

(14)

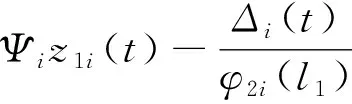
(15)

则体系上下部分的模态位移

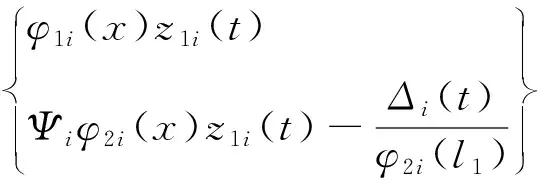
(16)

即断层在滑移运动情况下，形状函数φi(x)不连续，不满足式(3)经典阻尼体系的充要条件，体系不再具有解耦模态，为非经典阻尼体系。

2.2 鞭梢效应现象

鞭梢效应是指在地震作用下，高层建筑或其它建(构)筑物顶部细长突出部分振幅剧烈增大的现象[11]。闫祥梅等[12]发现，对于顶部有突出物的高耸结构，由于沿高度方向刚度和质量分布不均，尤其是下部主体与突出部分刚度和质量突变处，当遭遇大风等动荷载时，极易出现鞭梢效应。研究[13-14]发现，结构受风振时，突出部分的振动反应有时可以是主体结构的数十倍甚至更高，这是由于鞭梢效应的影响使得结构顶点的位移大幅度增加。本文从运动状态来分析这类现象的阻尼体系。

建立鞭梢效应的分析模型如图3所示。

体系由两部分连续质量m1(x)和m2(x)组成，且上部分m2的质量和刚度明显小于下部分m1的质量和刚度。设两部分单独运动特性具有经典阻尼体系特性，又其体系在连接处黏结强度足够，振动过程中位移在变截面上下位置处可保持连续，不会出现滑移运动。由3.1可知，若该体系仍可假设具有连续的形状函数和广义坐标，则模态运动位移可由式(17)表达

ui(x,t)=φi(x)z1i(t)

(17)

图3 顶部有突出物的高层建筑模型

其中，

(18)

然而，贾水钟[15]分别用SAP2000和ABAQUS对常州现代传媒中心一主塔高度245 m、其上有88 m高钢结构发射塔的高耸结构，进行了常遇地震和罕遇地震两种工况下的时程分析，得到其弹性和弹塑性时程分析下的层间位移角分别如图4和图5所示，其中主塔高度58层，故58层以下变形为主塔变形，58层之上为发射塔变形。不同工况下的研究结果均表明，该体系出现了明显的鞭梢效应，顶部细小突出部分的振动位移突变增大。

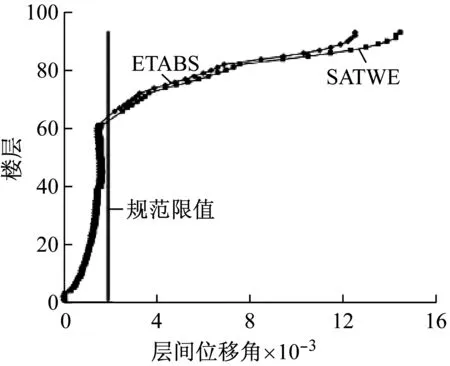
图4 鞭梢现象弹性时程分析

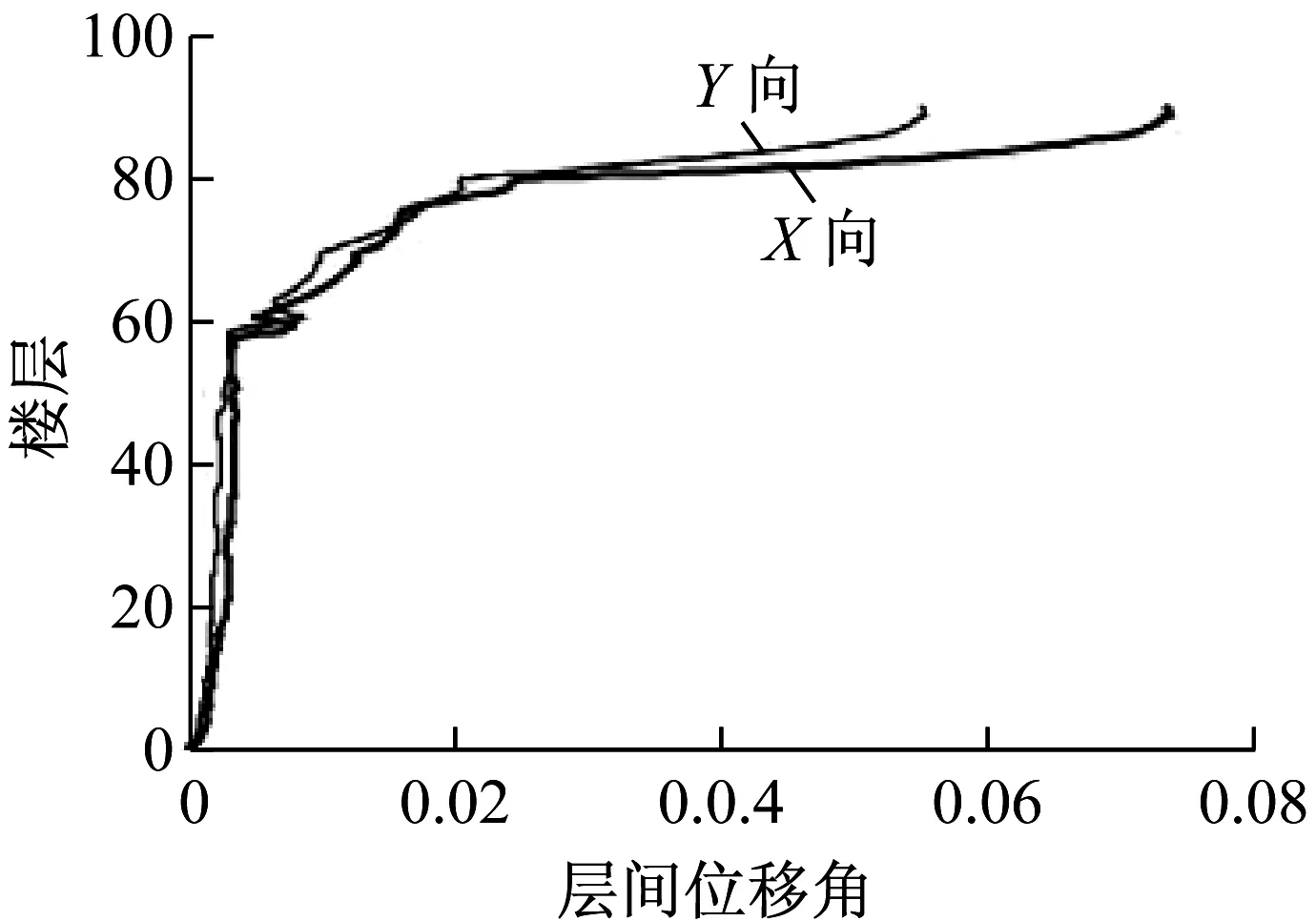
图5 鞭梢现象弹塑性时程分析

因层间位移为层间位移角与层高之积，故层间位移与层间位移角变化趋势相同。由图4和图5变化趋势可以看出，体系的层间位移曲线在主塔与发射塔相连部分出现明显拐点，最大层间位移发生在主塔与发射塔相连处。

为了进一步考察鞭梢现象，本文项目组针对顶部带塔楼的结构体系进行了振动台试验，试验过程中，塔楼与主体结构保持接触面位移连续，试验模型如图6所示。

图6 振动台模型试验

图7(a)和图7(b)分别给出了不同地震等级下，塔楼与主体结构各层的位移响应时程。

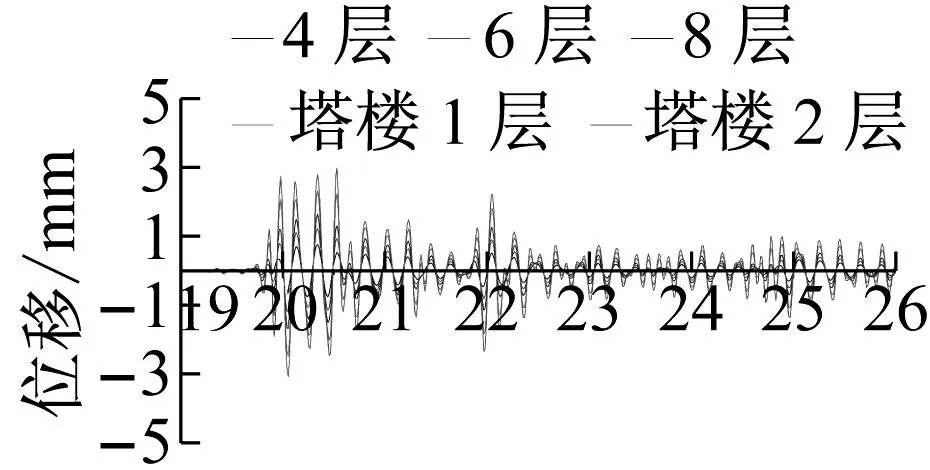
(a) 小震下 (台面输入加速度0.125g)

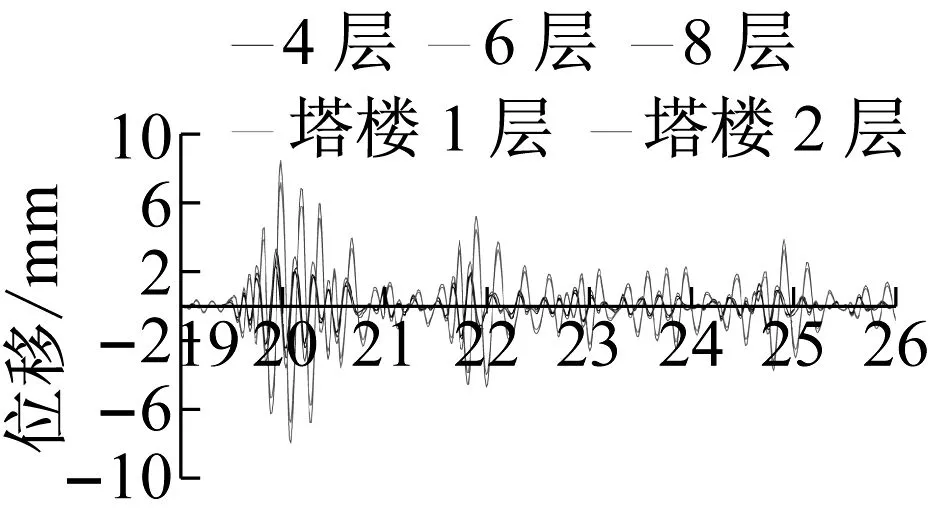
(b) 大震下 (台面输入加速度0.75g)

由图7知，在小震下，塔楼和主体结构基本能同时达到最大位移，运动保持协同一致；而在大震时，虽然塔楼和主体结构两部分能各自保持较好的协同运动，但体系整体运动步调不再协同一致。

现分别提取不同地震量级下，主体结构和塔楼顶层的速度响应时程曲线，如图8所示。

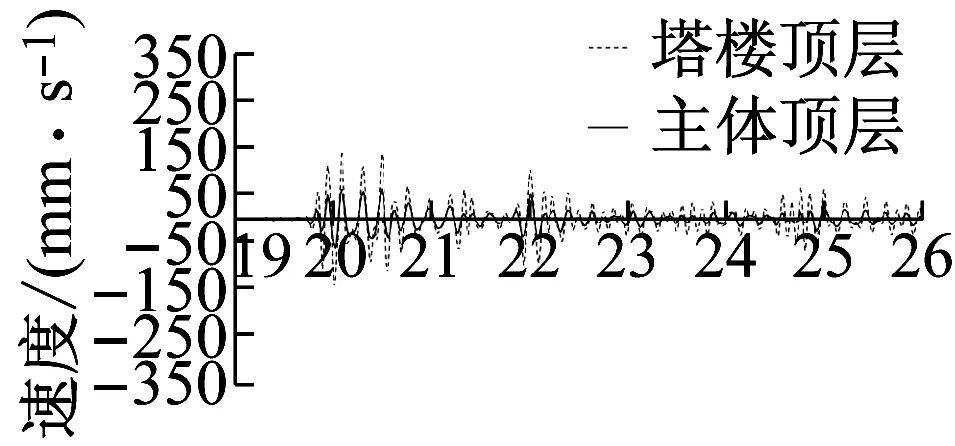
(a) 小震下 (台面输入加速度0.125g)

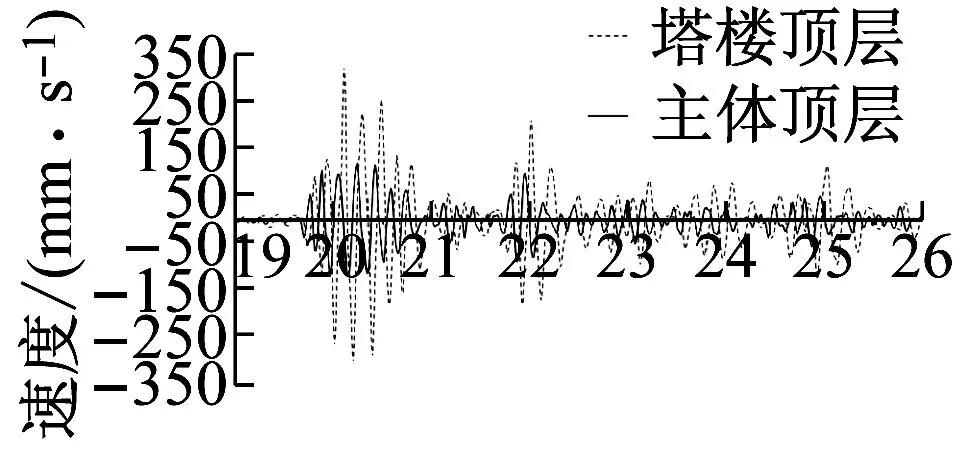
(b) 大震下 (台面输入加速度0.75g)

图7和图8结果表明，当振动量级较小时，塔楼顶部最大位移为主体顶部最大位移的2.27倍，如图7(a)所示，塔楼顶最大速度为主体结构的2.32倍, 如图8(a)所示，由鞭梢效应定义，体系未出现鞭梢效应，此时塔楼和主体结构各层测点基本同时达到最大位移，上下两部分运动协同一致。当振动量级较大，塔楼顶部达到峰值位移时，塔顶位移为主体顶位移的7.35倍，如图7(b)所示，而塔楼顶峰值速度为同时刻主体结构的15.21倍，如图8(b)所示，体系出现鞭梢效应。此时塔楼与主体结构各层测点不能同时达到最大位移，且塔楼和主体结构的运动不再协调。

这一现象表明，若体系未发生鞭梢效应，其运动存在模态，任意一阶的解耦模态可由式(3)表达为连续的形状函数和统一的广义坐标乘积的形式，整体运动协调一致。

当发生鞭梢效应时，上下两部分的振动频率不再相同，表现在模态上，必存在一阶或几阶模态运动的广义坐标不同，即

z1i≠z2i

(19)

式中：z1i,z2i分别为主体结构和塔楼的第i阶广义坐标。

此时，虽然连接位置处的位移、速度、加速度均连续，但塔楼部分第i阶模态运动不再能由主体结构模态运动的广义坐标z1i(t)表示，即

(20)

现分析发生鞭梢效应时界面处的运动状态，由于界面处黏结强度足够，不会出现滑移现象，因而界面上下位置处的运动位移连续，而界面以上部分速度不再符合主体结构的速度变化规律，即

(21)

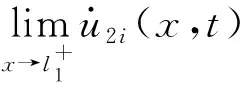
由于在接触面处形状函数连续，故广义速度在接触面处不能相等

(22)

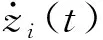
2.3 半主动控制中的加速度放大效应

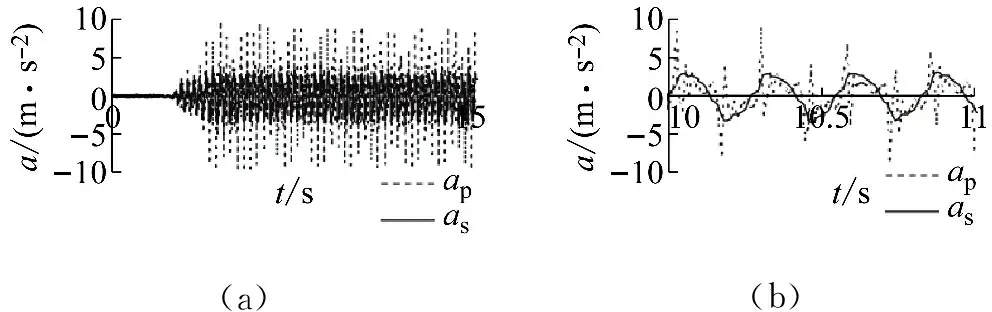
半主动控制[16-17]指控制力随体系运动而被动产生，其控制装置大多为各类可调节阻尼器，控制过程中，控制力可利用外加能源主动改变大小，从而调整体系动力响应。半主动控制以其控制效果接近于主动控制而仅需极小能源的优点成为近年来振动控制研究的热点之一[18]。本文为分析方便，取图9所示半主动控制结构讨论，其A，B，E，F处与地面采用滑动支座连接，C，D与地面采用固定支座连接。亓兴军等研究发现，在地震作用下，当半主动控制阻尼器设置在体系的非刚性支座处(图9中的A，B，E，F处)时，在纵向地震作用下，阻尼器附近局部位置的加速度会产生如图10所示的“针尖”放大效应，即加速度突变，而位移和弯矩却未出现明显的突变；当阻尼器设置在体系刚性连接处(C，D处)时，该放大效应不会出现。此外，香港理工大学Chau等[19]研究发现，动力作用下，桩土间可能出现间隙，如图11所示，并在后续运动中发生碰撞。且实测发现，桩体的加速度时程曲线在碰撞瞬间也会出现“针尖”放大效应，如图12(其中：ap为桩体的加速度；as为桩周土体的加速度)。这两类工程现象都被判定为非经典阻尼体系[20]。其共同特点是，在体系运动过程中，主体结构均突然受到来自外界的力的作用，加速度在时程曲线上呈现突变。

图9 半主动控制结构体系简化模型

Fig.9 Simplified model with semi-active controlling system

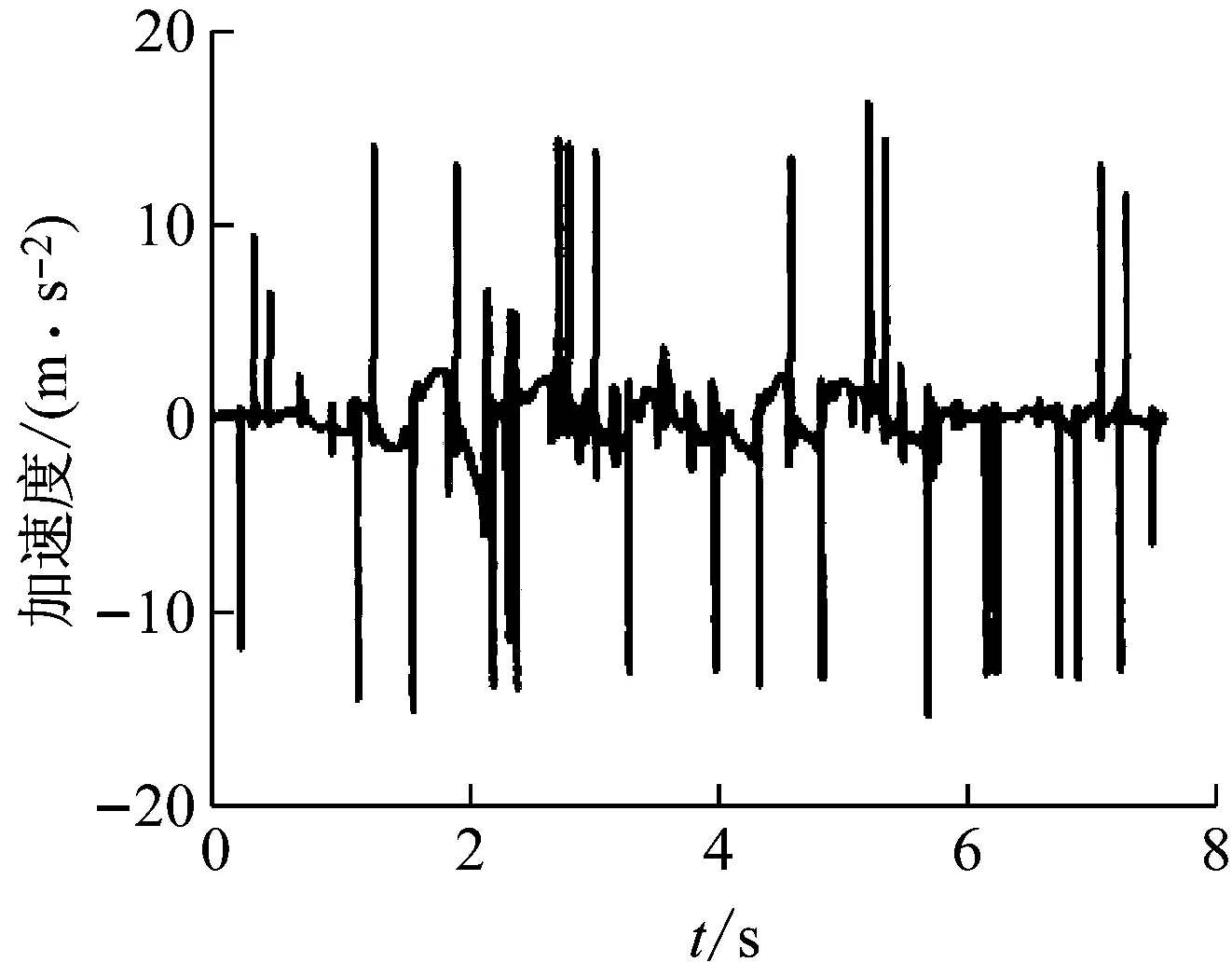
图10 加速度 “针尖”放大效应

图11 土-桩碰撞实地照片

(a)(b)

图12 桩体加速度“针尖”放大效应

Fig.12 Pinpoint-like acceleration magnified effect of the pillar

设半主动控制阻尼器设置在非刚性支座处用以调节体系的运动。在阻尼器发生作用之前，该体系为经典阻尼体系，其运动状态可由若干模态的线性组合形式表达，即体系位移、速度和加速度函数可表达为

(23)

在纵向地震作用下，当半主动控制阻尼器在非刚性支座处发生作用时，相当于该瞬时在支座处施加了纵向作用力，而该支座沿纵向并不能提供约束，因而在该力作用瞬间，该部位的局部纵向加速度突然增大。此外，因位移是加速度关于时间的二阶积分，弯矩是位移关于长度的二阶微分，体系内一点加速度突然增加，导致其位移函数曲线出现拐点，但位移不会发生突变，则弯矩也未出现突变。

即对体系的运动来说，当半主动阻尼控制力出现时，在非刚性支座处加速度发生突变，即速度函数出现不光滑，表现在模态上，加速度函数已无法表达为半主动控制阻尼器未发生作用时的原形状函数与广义坐标加速度乘积的线性组合，在非刚性支座处，体系的模态运动加速度不相等，即

⟹

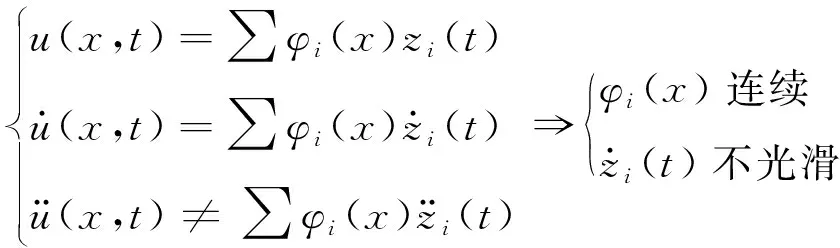
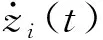
3 结 论

本文研究表明，运动状态的连续与否是经典与非经典阻尼体系的直接决定因素，形状函数连续和速度光滑连续，是经典阻尼体系的充要条件，非经典阻尼体系必将表现在运动状态中某一个变量发生突变。在此运动状态连续性理论研究基础上，本文分析讨论了实际工程中的地震断层滑移现象、鞭梢效应现象以及半主动控制器作用时，体系的运动状态及其相应的阻尼体系特性，希望能为工程阻尼体系类别的合理判别、合理择取结构动力分析方法提供基础理论参考。