基于泊松分布的集成电路寿命计算*

张 颖,王建业,,王海龙,,张家亮

(1 空军工程大学防空反导学院,西安 710051;2 空军工程大学信息与导航学院,西安 710077)

0 引言

在当今信息时代,伴随着电子技术的不断发展,集成电路在各系统中的应用越来越广泛。集成电路的平均无故障时间(MTBF)直接影响到系统的稳定性,如果集成电路在系统中失效,可能会造成不可估量的损失。因此集成电路的平均无故障时间受到了工程技术人员的广泛关注。

通常电子产品的平均无故障时间计算有三种方法:1)可靠性预计计算。主要是在设计之初设计者根据客户要求选择合适的方式和材料对产品进行设计。2)实验室试验和计算。主要是生产单位通过实验室试验对产品进行可靠性寿命评价。3)现场失效数统计计算。主要是对于投入市场的产品,通过对维修率的统计,求出MTBF的大致水平。

为计算集成电路的平均无故障时间,文中提供了一种较为通用的计算集成电路平均无故障时间的方法。

1 浴盆曲线

浴盆曲线是指产品从投入到报废为止的整个寿命周期内,其可靠性的变化呈现一定的规律。大量实践证明大多数集成电路的故障率是时间的函数,典型故障曲线称之为浴盆曲线(Bathtub curve,失效率曲线),该曲线的形状呈两头高,中间低的特点,具有明显的阶段性,其形状如图1所示。该曲线是以使用时间为横坐标,以失效率为纵坐标的一条曲线,产品随使用时间变化分为三个阶段:早期失效期、偶然失效期和损耗失效期。因该曲线两头高,中间低,有些像浴盆,所以称为“浴盆曲线”。

图1 浴盆曲线示意图

1.1 早期失效期

第一阶段是早期失效期,在这一阶段失效率很高,失效的主要原因是由于设计、原材料和制造过程中的缺陷造成的。为了缩短这一阶段的时间,产品在投入运行前应进行试运转,及早发现问题,剔除不合格的产品。

1.2 偶然失效期

第二阶段是偶然失效期,这一阶段的失效率较低,且较稳定,往往可以近似看作常数,产品可靠性指标所描述的就是这个时期。这一时期的产品处于良好的使用期,如果出现故障,大部分是由于使用不当和环境影响等造成的。

1.3 损耗失效期

第三阶段是损耗失效期,这一阶段的失效率随时间延长而急速增加,主要由磨损、疲劳、老化和损耗等原因造成,一般系统要求十年以上的损耗期[1]。

2 验证集成电路使用寿命服从泊松过程

文中所提供的算法都是基于以下假设:1)故障率函数为浴盆曲线;2)集成电路的使用寿命服从泊松过程。假设1)已经在1中进行了叙述,因此需要对假设2)的成立进行验证。

2.1 指数分布

对所需验证的数据进行采集,所采集的产品数据若能近似看作是与分布函数一致,通过分布函数的性质可以预测故障发展趋势和寿命分布规律。目前常见的累积分布函数有指数分布、威布尔分布、正态分布、对数正态分布等。因此根据采集数据,首先要分析研究故障发生规律,找出以时间作为随机变量的故障变化,看其是否符合某一种累积分布函数。

指数分布是一种常见的累积分布规律,它有几个显著的特点:故障率具有可加性,若系统中零部件失效率服从指数分布,则系统的失效时间也服从指数分布;故障率是一个与时间无关的常数;概率论中已证明指数分布是唯一的具有“无记忆性”的连续分布。而多数的电子设备及电子元器件的失效基本都属于指数分布,下面来进行验证2)。

以15个集成电路74HC00的一组故障时间数据来验证集成电路使用寿命的累积分布函数服从指数分布。文中以该集成电路的故障时间作为寿命数据,表1给出了该集成电路的故障时间tn(i),并按由小到大的次序排列,经验分布函数值的数学期望公式为:

(1)

式中：n为实验样本个数；i为按失效顺序排列的失效样本序号。

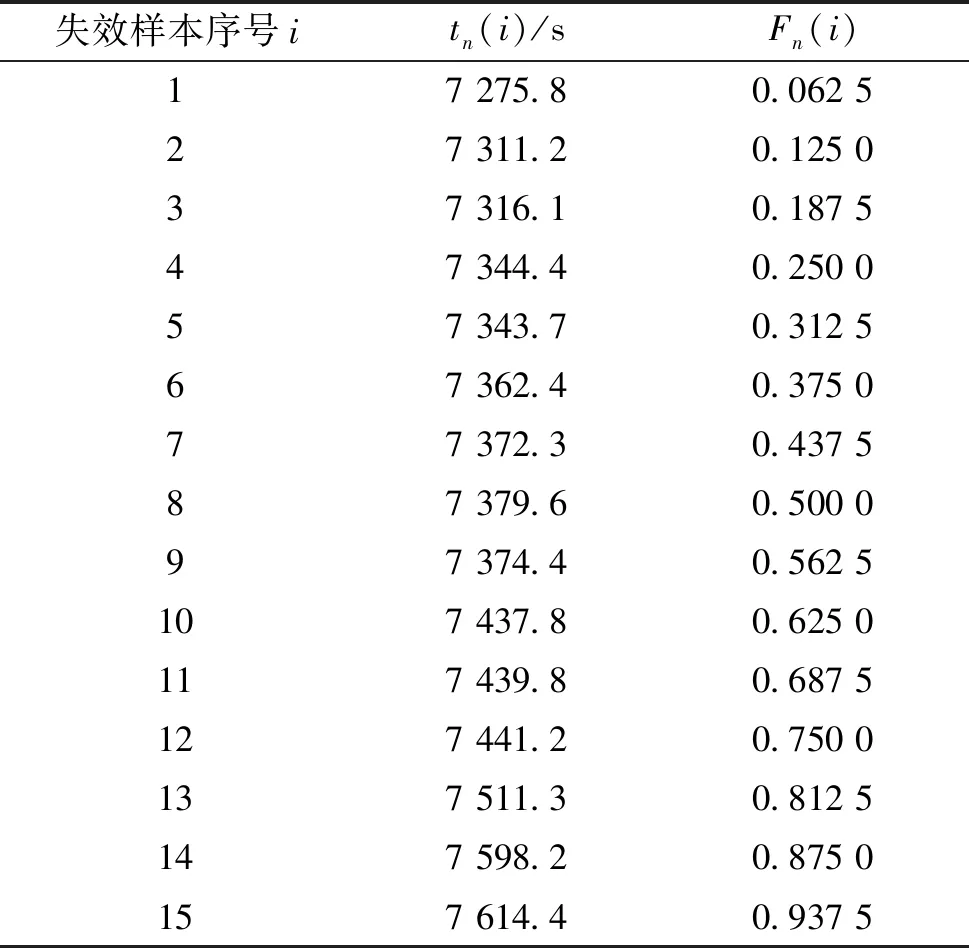
表1 74HC00的故障时间

指数分布函数为:

(2)

将其整理并取对数：

(3)

令：

(4)

变换后得到标准直线方程为:

y=ax+b

(5)

将表1中的数据Fn(i),tn(i)代入方程中可以得到yi,xi,见表2。

利用公式：

(6)

将得到的数据代入公式：

(7)

求得相关系数γ=0.980 6。

表2 变换后的xi和yi

由于相关系数γ是绝对值小于等于1的无量纲统计量,|λ|的值越接近1,线性关系越明显。本例中求得γ=0.980 6,非常接近1,因此可以认为该集成电路使用寿命的累积分布函数是指数分布函数[2]。

2.2 泊松过程

泊松过程是描述随机事件发生的基本数学模型之一,实际生活或自然界中的随机事件大多可以用泊松过程来描述。

输入过程是一个参数为λ的泊松过程的充要条件:相继到达间隔Ti(i=1,2,…),相互独立,且均服从参数为λ的指数分布。

(8)

在2.1中已经验证集成电路使用寿命的累积分布函数满足指数分布函数,而且相同类型的不同集成电路是否失效可以认为是相互独立的。因此,集成电路的使用寿命这一随机过程可以被认为是泊松过程[3]。

3 集成电路使用寿命的计算

文中所提供的计算使用寿命的算法只适用于故障率函数为浴盆曲线且使用寿命服从泊松过程的产品。前面的叙述已经证明集成电路的使用寿命问题是满足这两个条件的,因此可以采用下面的算法来计算其使用寿命。

3.1 浴盆曲线故障率函数

基于已有的研究成果,基于浴盆曲线的故障密度函数有如下形式:

f(t)=γβ(t/α)β-1exp{(t/α)β+γα(1-e(t/α)β)}

(9)

对应的故障率函数:

λ(t)=γβ(t/α)β-1exp{(t/α)β}

(10)

可靠度函数:

R(t)=exp{γα(1-e(t/α)β)}

(11)

图2 故障率曲线

从图2可以看出,产品的故障率明显呈浴盆曲线特性,可以用来描述分布特征为浴盆曲线的产品的故障率。

3.2 MTBF的求解

通常用于评价集成电路使用寿命的指标为平均无故障时间(MTBF),因此文中使用MTBF来衡量集成电路的使用寿命,根据MTBF的定义可以得到以下关系式:

(12)

仍然以集成电路74HC00为例来计算该集成电路的MTBF。因为其故障率服从浴盆曲线特征,所以可以利用浴盆曲线的故障密度函数构造最大似然函数,估计分布参数,构造似然函数。

(13)

利用表1中的数据,通过方程组：

(14)

解得α=0.8,β=0.03,γ=1.5,所以:

λ(t)=0.045(t/0.8)-0.97exp[(t/0.8)-0.03]

R(t)=exp[1.2(1-e(t/0.8)0.03)]

代入到MTBF的定义式中可以得到MTBF=7 426 h。

一种集成电路工作了较长时间(一般时间是十几年)就会进入损耗期,该电路会出现损坏。根据给出的一组故障时间的数据,得到的预测数据与该集成芯片的实际使用情况相接近,说明文中所提供的算法具有一定的实用性,达到了预期目的[4]。

4 结论

文中提供了一种计算集成电路平均无故障时间的一般性方法,为电路系统的可靠性分析提供了依据。相比于已有的计算集成电路平均无故障时间的方法,所提供的方法具有通用性,只需满足计算所需要的条件,并提供相应集成电路的一组故障时间,就可以分析计算得到其平均无故障时间,这种预测对于可靠性要求较高的系统具有很重要的参考意义,可以提前对元器件进行检测,防止发生故障[5]。下一步将研究其他衡量集成电路平均无故障时间的指标的计算方法,预测同一集成电路在不同的平均无故障时间指标下的值,综合分析这些数据,从而得到更加精确的预测值。