航天器传动部件振动数据稀疏多分类智能故障诊断
2018-08-27陈彬强何昱超贺王鹏
陈彬强,何昱超,姚 斌,王 栋,贺王鹏
(1.厦门大学 航空航天学院,厦门 361005; 2.北京卫星环境工程研究所,北京 100094;3.西安电子科技大学 空间科学与技术学院,西安 710071)
0 引言
随着航天器结构的复杂化和综合化[1],基于传统可靠性工程的诊断方法已经难以适应其传动部件故障诊断的需求。近年来,数据驱动的航天器机械、控制等子系统的状态监测理论和方法成为了研究热点[2]。王国彪等从监测数据获取、数据处理方法、故障模型建立、决策方法等方面提出了新见解,提高了故障识别能力[3]。在信息采集及感知方面,谢文杰等设计了被动式网络数据监控方案,为航天测控网数据监控、性能评估、故障诊断提供有效手段[4]。吴东亮等建立了大型航天器真空热试验过程管理系统[5]。李海飞等对两器分离阻力进行了建模、测量与验证[6]。在数据分析方法和智能决策方面,陈彬强等提出了非传统的双密度双树复小波变换,提高了故障特征识别能力[7]。贺王鹏等提出周期稀疏导向超小波,实现了“频率-尺度”平面上高度柔性的时频特征提取[8]。Henry等提出了一种高鲁棒性的航天器推进装置模型驱动故障诊断方法[9]。葛强强等提出一种基于深度置信神经网络,实现航天器轴承一周训练数据的故障诊断方法[1]。
虽然以上研究都从某些问题入手取得了进展,但针对航天器传动部件的突出问题,即如何在装备非拆卸状况下利用尽可能少的传感器及动态数据进行分析并识别出多种故障模式,仍然没有得到较好的解决[10]。另一方面,当航天器内部复杂机电装置内零部件发生损伤时,其故障特征往往呈现较强的非线性和非平稳性,采用传统的数据处理方法往往得不到正确的结果[11]。
针对以上问题,本文从两个方面进行诊断性能提升:一方面,采用性能优越的现代时频信号处理方法——分形小波(fractal wavelet)[12];另一方面引入多尺度信息的增强后处理方法——稀疏多分类。基于以上改进,提出一种振动数据驱动的传动部件故障多稀疏评价及多分类识别算法。在技术路线上,对所监测的传动部件进行动态数据采集;对单一传感器的动态数据进行分形小波分解;按照故障特征频率对各小波尺度进行故障稀疏评价指标计算;根据故障频率的最大值判定故障类型。最后,在轴承故障模拟试验台上模拟航天器轴承可能出现的故障类型,对提出方法进行有效性验证。
1 分形小波变换
1.1 分形小波变换基本理论
令采集得到的动态信号x长度为L。为了对x实现分形分解,采用基于近似解析的复小波基函数,该基函数具有一个复值尺度函数

和一个复值小波函数

式中:φRe(t)和φIm(t)代表复尺度函数的实部和虚部;ψRe(t)和ψIm(t)代表复小波函数的实部和虚部。
而对应的滤波器组存在半采样延迟,即:

式中h(·)(n)和g(·)(n)分别代表尺度函数和小波函数对应的滤波器。在任意尺度上,两尺度相似关系依然成立,即:

式中变量j为分解深度。
满足以上条件所构造的小波基可以满足正交性、近似线性特性,对单位冲击脉冲信号的分解具有近似平移不变性,可以有效地抑制分解过程的能量泄漏。因此,相对于传统离散小波变换,复小波基可以有效增强动态数据中暂态成分的提取能力,被广泛应用于设备的故障诊断。
信号分形小波变换得到了一系列子空间,其中包含常规的二进子空间及再生尺度空间,其分解过程如下:
1)采用二进小波方法对原信号进行二进分解,得到小波尺度。
2)对高频小波尺度(带通滤波器及高通滤波器对应的尺度)进行二进再细分。对于一个k层近似解析小波包分解,共得到2k个小波包尺度,记为。
3)按照格雷码映射方法,对wpk,i进行重排列映射,记为。
在上述算法过程中,1)~3)生成了常规二进小波尺度,4)生成了非常规的二进小波尺度。所生成的非常规二进小波尺度保持了复小波基原有的优良特性。
1.2 分形性质刻画
采用1.1节算法生成的每个尺度都是定义良好的带通滤波器,可以用带通中心频率fc和带宽Δf来刻画。
按照索引下标k和i,可将分形小波的“频率-尺度”网格绘制于图1。其中“尺度0”代表原信号的滤波通带。深度为奇数(k=2m+1,m≥0)的尺度为非常规二进小波尺度,而深度为非负偶数(k=2m,m≥0)的为常规二进小波尺度。
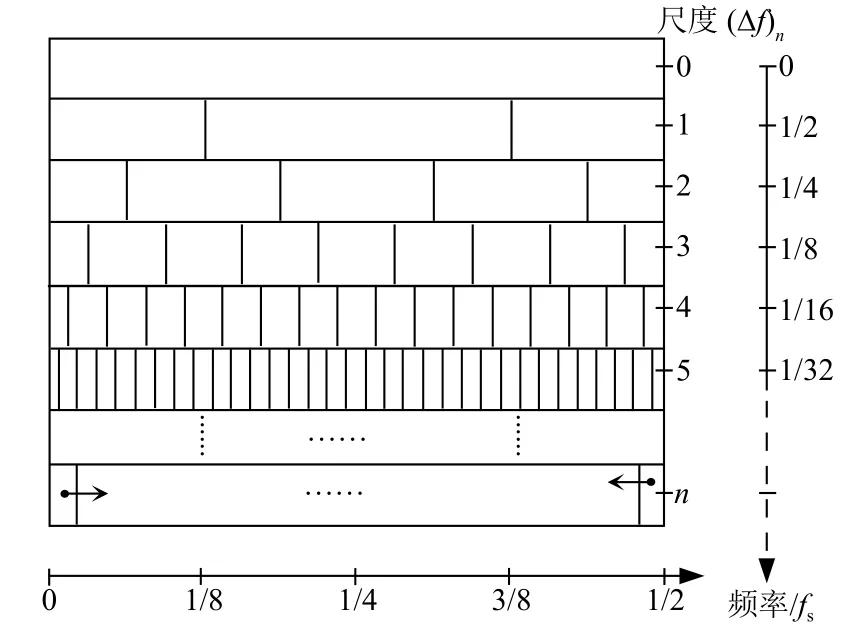
图1 分形小波变换的“频率-尺度”划分网格Fig.1 Frequency-scale paving of fractal wavelet
令原始信号的分析频率为fs/2 ,如表1所示,常规二进小波尺度和非常规二进小波尺度的中心频率和带通范围显著不同。

表1 两种不同尺度的参数Table 1 Parameters of two types of wavelet subscales
对比表1和图1可知,非常规小波尺度的带通中心频率恰好与常规二进尺度的带通上限频率或带通下限频率重合,能够弥补常规二进尺度的过渡带提取能力不足问题。
另外在图1中还可以发现,常规的二进小波包仅能实现尺度分辨率的逐渐细化,而非常规的二进小波包则可以实现围绕固定分析中心频率的分辨率细化,其细化方式与二进小波包相同。
2 基于故障能量指标的稀疏多分类器
为了使机械故障诊断不再依赖于诊断专家和专业技术人员,需要对设备进行高效的智能诊断。关键机械设备的故障智能诊断的主要任务是利用设备故障机理及运行过程中的动态特征信息,智能识别出机械设备安全方面存在的薄弱环节和故障,对设备的安全性能做出系统的评估。目前已有许多人工智能算法用于对多种故障模式进行智能分类,但这些算法往往依靠大量的训练样本数据。本文提出一种基于故障能量指标的稀疏多分类器。在使用该多分类器之前,应该知道特定工况下航天器传动部件的故障特征频率fch。
一些关键机械设备长期运行在重载、疲劳、腐蚀、高温等复杂恶劣的工况下,其核心零部件和重要机械结构将不可避免地发生不同程度的故障。滚动轴承是旋转机械中应用最为广泛的机械零件,也是最易损坏的零件之一,在恶劣环境条件下,极易发生点蚀、疲劳剥落和磨损等故障。因此,对滚动轴承损伤故障进行自动识别,预防重大事故发生,是机械故障诊断领域的一个重要研究方向。当滚动轴承的工作表面出现点蚀、剥落、擦伤等局部损伤故障时,损伤引起的振动信号呈现出振荡衰减的形状。当机械中的关键零部件出现故障时,信号中包含的故障信息往往都以调制的形式出现,即我们所测到的信号常常是被故障源调制了的信号。例如机械系统受到外界周期性冲击时的衰减振荡响应信号就是典型的幅值调制信号。要获取故障信息就需要提取调制信号。提取调制信号的过程就是信号的解调。当传动部件发生故障时,常出现周期性的暂态成分。为了定量描述动态信号子空间中故障成分的多寡,本文提出了故障能量指标的概念。其计算方法分为以下3步:
2)根据复信号计算小波包信号的包络谱;
3)在包络谱中,根据故障特征频率fch计算基频和高次谐波i·fch(次数i≤3)的能量比值E{fch}。
通过以上计算,故障特征集中的尺度故障能量指标的数值很高,实现了稀疏表示。稀疏多分类器主要功能是根据各特征频率的能量比值大小排序判定发生故障类型,方法如下:
1)根据部件可能发生的故障频率集合{fch,1,···,fch,m}分别计算各特征频率的故障能量指标E{fch,i}
2)选择E{fch,1},···, E{fch,m}中的最大指标作为该信号的故障能量指标,即;
3)根据故障能量指标所属特征频率确定实际故障类型。
3 稀疏多分类器算法
本文通过引入分形小波提高对信号非平稳和非线性特征的分析能力,引入故障能量指标驱动的稀疏多分类器改进了小样本传感器数据下的故障模式自动识别。
下面以航天器轴承的多种故障模式分类为例说明算法的整体流程。轴承的故障特征频率可以根据内圈旋转频率、轴承节径、滚动体直径、接触角、滚动体个数进行计算,对应的特征频率分别为保持架故障频率、滚动体自转频率、外圈故障频率、内圈故障频率和滚动体故障频率[12]。
结合本文的2种改进方法,提出的稀疏多分类器算法流程如图2所示。通常在靠近轴承的部位(如轴承座)安装传感器以获得故障特征敏感度高的动态信号,再按照图2的流程进行处理。

图2 智能故障诊断算法流程Fig.2 Flow-chart of the intelligent fault diagnosis algorithm
4 航天器轴承故障模拟验证
滚动轴承在航天发射回转平台、航天器机构关节和航空发动机中广泛使用。其部件常由于恶劣的工作条件(如重载荷、交变温度场等)而发生疲劳损伤。世界上航天发达国家记录了多起由于轴承失效而造成任务失败的案例[13-14]。针对航天轴承的疲劳和故障失效分析,目前采用的方法有摩擦学特性分析、摩擦力矩测试和温度测试等,但还无法达到满意效果[15]。本章论述基于振动信号对轴承故障进行的部件故障模拟和诊断实验。
为了验证所提出算法的有效性,在轴承转子试验台(见图3)上进行航天器轴承的故障特征提取试验。测试轴承由液压马达驱动,柱塞泵在滚动轴承的径向进行模拟加载。在转轴上安装了一个接近式测速计以便检测并反馈轴承的旋转速度。通过在测试轴承上采用线切割和电火花等手段人为模拟故障进行测试验证,结果发现轴承的外圈有一处轻微损伤,如图4所示。

图3 故障模拟试验台示意Fig.3 Set-up of the bearing fault simulation testbed

图4 加载装置及故障轴承图片Fig.4 Photographs of the loading device and the faulty bearing
被测试轴承型号为552732QT,其尺寸参数见表2,由此可以计算轴承各子部件的故障特征频率。根据轴承外圈故障频率计算公式其特征频率确定为78.169 Hz。

表2 被测试轴承的主要规格参数Table 2 Parameters of the test bearings
在轴承的外圈上模拟故障,控制轴承的转速为650 r/min(即旋转频率为 650/60=10.83 Hz)。振动加速度信号的采样频率为12.8 kHz,信号的采样长度为12 800。采集振动信号的波形如图5所示,而其对应的傅里叶频谱如图6所示。由图可见,时域波形的成分十分混乱,看不到显著的故障特征;频域的分辨率达到1 Hz,可以发现在低频段存在等间隔的变频带现象,而在频率大于1500 Hz的频段则主要为连续谱成分。

图5 振动信号时域波形Fig.5 Time domain waveform of the original vibration signal

图6 振动信号频谱Fig.6 Fourier spectrum of the vibration signal
采用本文提出的算法对该数据进行分析,结果如图7所示。其中出现了规律的周期性振荡衰减的冲击成分,冲击间隔为12.8 ms(将图7放大后,可以计算出故障特征频率的平均值为78.125 Hz),与轴承的外圈故障频率的理论值(78.169 Hz)十分接近。图8是由图7提取的故障特征频率计算而得到的包络解调谱,其中故障特征频率及其倍频(1~6倍频率)的能量十分集中。根据本文所提出的方法有效地提取了造成轴承外圈损伤的微弱周期性冲击故障成分。

图7 用本文算法提取的故障特征信号Fig.7 The extracted fault feature using the proposed method

图8 故障特征信号的包络解调谱Fig.8 Hilbert envelope spectrum of the extracted fault features
5 结论与展望
为了在小样本数据下对航天器传动部件动态信号中的微弱故障特征进行有效提取,并基于特征进行故障模式分类,提出了一种新的稀疏多分类智能算法,并对该算法的有效性进行了验证,结论如下:
1)引入分形小波,对比其中的常规二进小波尺度和非常规二进小波尺度的带通参数,证明后者可以弥补前者在过渡带边缘特征提取能力不足的缺点。非常规二进小波尺度在“频率-尺度”网格上可以实现围绕特定中心频率的频率分辨率细化。
2)引入定量描述信号故障特征含量多寡的稀疏评价指标,根据部件的故障特征频率计算其故障能量指标,通过指标数值寻找对应的故障类型进行稀疏多分类。
3)以航天器轴承为例,对所提出的故障诊断算法的有效性进行验证,模拟了轴承常见的故障类型。分析结果表明所提出算法可以正确定位并分辨实际故障类别。
本文所提出的算法同样适用于具有不同故障特征频率的复合故障诊断,还可以推广到航天器其他类型机械零部件的状态监测和故障预警,这方面的研究目前正在处于验证和完善阶段。