密封舱内漂浮小球运动规律的数值模拟研究
2018-08-27刘冬雨魏传锋
张 峤,刘冬雨,罗 超,魏传锋
(中国空间技术研究院 载人航天总体部,北京 100094)
0 引言
“天宫二号”空间实验室的实验舱内搭载了机械臂操作终端系统[1]。计划在空间实验室与载人飞船组合体飞行期间,航天员乘组与机械臂操作终端协同完成首次人机协同在轨维修技术试验,为航天员与空间机器人的人机协同作业积累在轨经验。
在正式的在轨维修试验之前,工程技术人员先期设计了机械臂操作终端在轨抓取小球的验证试验。在轨微重力环境下,密封舱内不存在自然对流,载人环境的建立需通过舱内强制通风来保证,这将导致漂浮在舱内的小球随流场运动,对机械臂操作终端抓取小球任务构成干扰项。
本文建立了密封舱内漂浮小球运动的物理模型与数学模型,采用动网格方法,对小球的运动速度和位移进行数值模拟,得到典型工况下小球的运动规律,并由此确立小球的设计参数范围,作为机械臂操作终端系统试验方案设计的依据。
1 计算模型
1.1 物性参数
实验舱内压力体制基本均衡(标称1个标准大气压),舱内通风气流速度不大于0.5 m/s,可将气流简化为不可压缩流体。计算所用物性参数如表1所示。

表1 计算所用物性参数Table 1 Physical properties of the sealed cabin for calculation
1.2 边界条件
通过分析,机械臂操作终端的机械手可对标准网球尺寸(φ=66 mm)的小球进行抓取,考虑到小球几何构型的轴对称性,将计算域简化为图1所示区域。

图1 计算区域示意Fig.1 Computational model and domain
由于气流已简化为不可压缩流体,所以可直接将左侧流场入口定义为速度入口,右侧定义为流场出口。进一步将自由空间简化为半径0.3 m(约为小球半径的10倍)的圆柱体计算域,边界为无滑移壁面。
1.3 控制方程
不考虑化学反应,对于单组分气相工质,流场控制方程如下[2-3]:

式中:ρ为流体密度;ui、uj分别为流体在x、y方向的速度矢量;p为流体压强;为雷诺应力;σij为黏性剪切应力,

其中,μ为分子黏性系数,δij为 Kronecker Delta,当i=j时δij=1,当i≠j时δij=0。
使用有限体积法将控制方程组离散为网格单元上的线性代数方程[4]。当计算对空间与时间分辨率要求不高时,直接采用雷诺时均模型(RANS),假定湍流中的流场变量由一个时均量和一个脉动量组成,引入Boussinesq假设,认为湍流雷诺应力与应变成正比,则湍流模拟可归结为对雷诺应力与应变之间的比例系数(即湍流黏性系数)的计算[3-5]。本文采用带旋流修正的两方程k-ε湍流模型对控制方程进行封闭,并利用增强壁面函数法处理流动中的近壁区域[6-7]。
1.4 动网格模型
使用动网格模型模拟流场形状由于边界运动而随时间改变的问题。网格的更新过程根据每个迭代步中边界的变化情况自动完成[5,8]。系统考虑式(1)~式(3),在任意一个控制体中,广义标量Φ的积分守恒方程为

式中:u为流体速度矢量;ug为移动网格的网格速度;Γ为扩散系数;SΦ为源项;∂V代表控制体V的边界。
方程中的时间导数项,可以用一阶后向差分格式表示为

其中n和n+1代表不同的时间层。
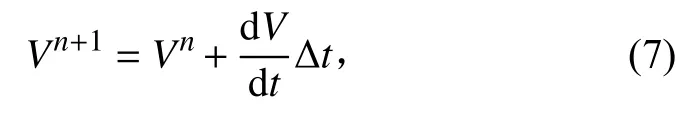
其中dV/dt是控制体的时间导数。为了满足网格守恒定律,控制体的时间导数可以表示为

其中:nf是控制体积的面网格数;Aj为面j的面积矢量;

其中δVj为控制体积中面j在时间间隔Δt内扫过的空间体积。
微重力环境下,忽略小球所受重力,来流对小球的作用力驱使小球随动,作用在小球壁面上的力Fi包含压强效应和黏性剪切力2部分,即
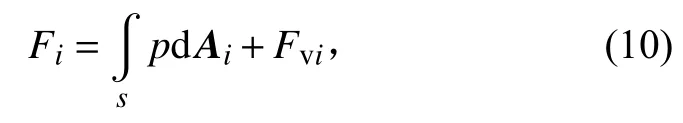
式中Fv即为黏性力,由近壁函数求得,i代表空间矢量分量。由于来流速度较低,所以压强效应与黏性剪切力的比例相当,黏性力不可忽略。
由小球表面的作用力,可推知当前时刻小球在流场中的加速度,则下一时刻小球的运动速度及位移可表示为:
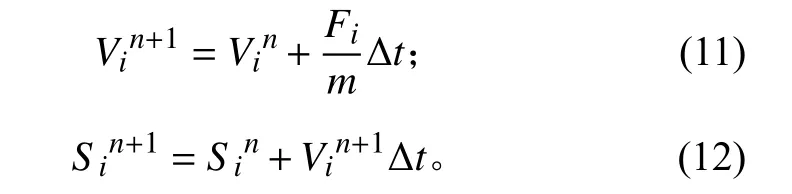
将小球视为刚体,通过编写用户自定义函数(UDF),调用Define_CG_Motion宏,对小球的运动方式进行描述[4-5]。
与方形结构相比,小球构型不甚规则,为了避免小球移动过程中出现负体积网格,采用弹簧顺滑动网格模型实时更新流场,使用非结构网格对整个计算域进行离散,初始网格数量为27 200。
1.5 离散格式
对动量方程使用二阶迎风格式进行离散,对湍流方程使用一阶迎风格式进行离散。动网格计算中采用一阶迎风格式对时间项(式(6))进行离散,步长为0.005 s,共计算20 s。非稳态流场压力-速度的耦合求解采用PISO算法[9-10]。
2 计算结果与分析
2.1 流场特性分析
将小球质量m=58 g(标准网球重量)、来流速度v=0.1 m/s的工况定义为基准工况,对基准工况进行计算,不同时刻下的计算域网格如图2所示。可以看出,计算网格随着时间的推移而重构:网格边界移动前由“弹簧”组成的系统处于平衡状态;在网格边界节点发生位移后,节点位移形成的力破坏了“弹簧系统”原有的平衡,系统经过调整将达到新的平衡,即在新的位置上重新获得受力平衡,据此经过迭代计算,得到使各节点上的合力等于0的、新的网格节点位置。当运动边界的位移远远大于网格尺寸时,为了避免因网格畸变过大导致计算不收敛,须将局部网格重新划分或合并,用新的网格代替原来的网格。

图2 基准工况中网格随时间的变化Fig.2 Sequence of gird variations in the basic calculation case
与图2对应的速度幅值云图如图3所示。在t=0时刻,小球处于准稳态,其左右两侧的受力均匀,没有运动速度;随着自由来流撞击小球,小球被流场驱动。通过图3(b)、3(c)可以看出,由于自由来流的黏性特征,小球背风面将出现由逆压梯度带来的不断脱落的旋涡区。图4给出了图3对应的流线图,展现了小球背风区的旋涡形状。脱落的旋涡将会导致背风面压力不稳定,因此小球表面受力将会呈现周期特性。

图3 基准工况中不同时刻速度幅值云图Fig.3 Velocity contours in the basic case

图4 基准工况t=10 s时刻背风区流线图Fig.4 Streamlines in the basic case at t=10 s
2.2 小球运动特性分析
2.2.1 计算工况
为系统研究小球在自由来流流场中的运动规律,下面分别以小球质量及来流速度为变化参数,对表2所示的10组工况进行仿真分析。

表2 计算工况设置Table 2 Parameter settings for the calculation cases
2.2.2 小球运动特性
小球速度随时间变化规律与受力变化规律一致,在受力转入振荡状态之前,速度曲线斜率较大;当受力转入振荡状态之后,速度斜率下降,基本呈现匀加速特性。将速度曲线积分可得到位移曲线。由于小球运动速度不断加快,所以位移随时间推进而快速增大。
对工况1~工况5进行系列计算,小球受力、运动速度和运动位移随时间变化规律分别如图5、图6和图7所示。可以看出:作用在小球表面的力存在一个明显的启动峰,来流速度越大,启动峰越明显;当小球刚刚启动时,作用力较大,亦即加速度较大;随着小球在流场中被“带着”移动,小球所受作用力呈逐渐下降的趋势,这是由于小球自身惯性所产生的滞后效应而导致的。还可以看出,随着来流速度的增加,小球表面作用力迅速转捩到振荡状态。结合2.1节的流场特性分析可知,振荡受力正是由于小球背风区旋涡脱落导致的。
对工况6~工况10进行系列计算,小球受力、运动速度和运动位移随时间变化分别如图8、图9和图10所示。经过对比可以看出,500 g小球的受力特性与58 g小球的基本相同,均呈现出启动峰-稳态-振荡状态3个分部区域;不同之处在于500 g小球的惯性比58 g小球大,因此受力曲线转入振荡状态的时间点后移,小球运动滞后特性更加显著,导致振荡周期变长。

图5 58 g小球受力随时间变化的计算结果Fig.5 The force on the floating ball of 58 g

图6 58 g小球速度随时间变化的计算结果Fig.6 Velocity characteristics of the floating ball of 58 g

图7 58 g小球位移随时间变化的计算结果Fig.7 Displacement characteristics of the floating ball of 58 g
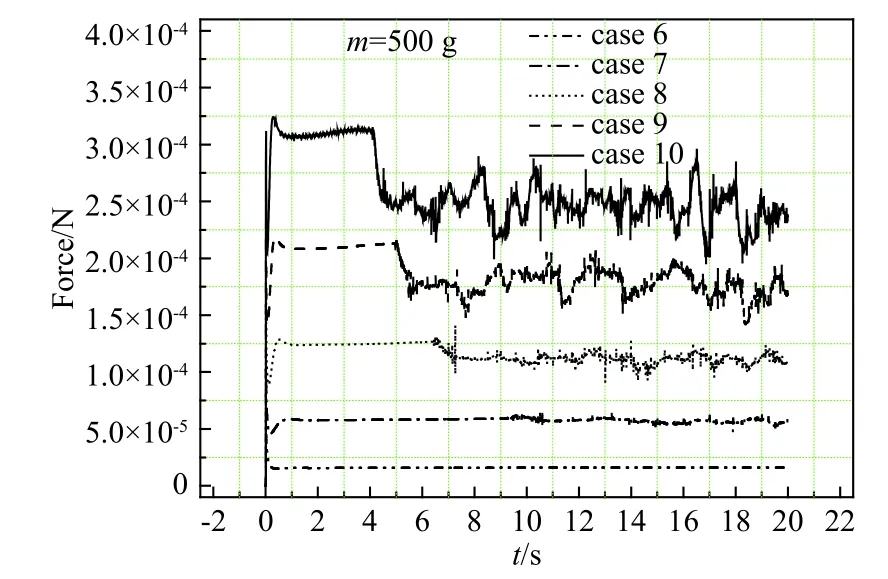
图8 500 g小球受力随时间变化的计算结果Fig.8 Calculated force on the floating ball of 500 g against time

图9 500 g小球速度随时间变化的计算结果Fig.9 Calculated velocity of the floating ball of 500 g against time

图10 500 g小球位移随时间变化的计算结果Fig.10 Calculated displacement of the floating ball of 500 g against time
2.3 分析结果
对2.2.2节中小球运动的关键数据进行提取,形成表3。对比两种小球的运动速度及位移变化曲线得出,在运动末期500 g小球的速度及位移均约为58 g小球的1/7。可以看出,当最大来流速度为0.5 m/s时,标准网球重量的小球在10 s时的运动位移将超过400 mm,此种情况下机械臂操作终端捕获小球的成功率将大大降低。综合考虑机械臂操作终端的运动速度、机械手抓取速度及视觉相机视场特性, 用于在轨试验的小球的质量应不小于500 g,抓取小球试验的有效时长应不长于20 s。

表3 小球运动关键数据Table 3 Key parameters of ball motion
3 在轨试验
2016年10月—11月,“神舟十一号”航天员乘组驻留“天宫二号”空间实验室期间,机械臂操作终端完成了2次抓取500 g漂浮小球试验任务,均一次性成功。图11展示了漂浮小球从静止到运动10、20 s的图像。将小球尺寸(φ=66 mm)作为标准刻度进行对比可以看出,小球在10 s时刻的运动距离为54.9 mm,20 s时刻的运动距离为185.5 mm,与图10、表3中500 g小球在0.5 m/s的舱内来流速度下的仿真预示值吻合程度较高,初步验证了本文计算结果的正确性。

图11 小球在轨运动图像Fig.11 Movement of floating ball in-orbit
图12给出机械臂操作终端在轨抓取漂浮小球的始、末画面,试验取得成功。首次人机协同在轨维修技术试验,为航天员与空间机器人的协同作业积累了在轨经验,为提高空间站机械臂精细操作能力和控制鲁棒性提供了在轨基础方法和参数。

图12 机械臂操作终端抓取漂浮小球试验图像Fig.12 Pictures of floating ball caught by space manipulator terminal
4 结束语
本文采用CFD动网格方法,对密封舱内漂浮小球在轨随来流的运动规律进行了数值模拟,得到了小球的受力、运动速度和位移随时间变化的规律。研究结果表明:小球在载人密封舱内通风流场中的运动呈现非线性特性;质量较大的小球在流场作用下转入振荡状态的时间点后移,小球运动滞后,振荡周期变长。
通过研究,工程技术人员得到了小球的设计参数范围,作为机械臂操作终端系统试验方案设计的依据。“神舟十一号”航天员乘组驻留“天宫二号”空间实验室期间,机械臂操作终端完成了抓取漂浮小球的试验任务,初步验证了本文计算结果的正确性。