TTI介质纯准P波一阶压力-速度方程及求解方法
2018-08-24李佳珂张会星张建敏
李佳珂,张会星,白 冰,张建敏
(1.中国海洋大学 山东 青岛 266100; 2.海底科学与探测技术教育部重点实验室,山东 青岛 266100)
0 引言
地球是一个非均匀、广泛存在各向异性的介质体。其中具有倾斜对称轴的横向各向同性(Titled Transverse Isotropic,TTI)介质作为描述地层中各向异性介质最具一般代表性的模型[1],受到了地球物理勘探界的广泛关注。研究TTI介质中地震波的传播规律对于提高裂缝性地层的地震勘探精度具有重要意义[1-10]。
前人已对于声学各向异性理论进行了大量的研究。Alkhalifah[11-12]首先提出了著名的声学假设:即将沿对称轴方向的剪切波速度设置为零,并基于该理论推导了具有垂直对称轴的横向各向同性(Vertical Transverse Isotropic,VTI)介质四阶伪声波波动方程;吴国忱等[13]在频率—空间域试算了该四阶伪声波方程的数值解;Du等[14]对方程进行化简,引入辅助函数,推导出VTI介质二阶伪声波波动方程;Duveneck[15]通过变换弹性张量中的系数,使得辅助波场具有实际的物理意义,也获得了相应的VTI耦合准P波方程;Hestholm等[16]通过引入辅助参数,推导出了VTI介质下耦合准P波方程的一阶形式;韩令贺和何兵寿[17]针对该方程,利用高阶交错网格有限差分进行了求解;Zhou[5]、Fletcher[6-7]将VTI介质二阶方程推广至TTI介质;Flowler等[18]研究发现该类耦合波动方程都是等价的,并给出了TI介质二阶耦合准P波方程的一般形式。然而,实际模型试算结果表明,该类TTI介质耦合波动方程存在菱形伪横波干扰噪声,对各向异性介质中准P波传播规律产生影响;在Thomsen参数δ>ε时,方程难以稳定求解;此外当TTI介质空间各点的对称轴倾角陡然骤变时,方程会产生数值不稳定的现象[8]。
近年来,针对消除声波方程中的伪SV波,国内外学者们给出了几种不同的各向异性介质准P波方程。Xu等[19]通过把拟微分算子分解为标量算子和微分算子,实现对各向异性介质声波方程相速度的控制,由此推导出VTI介质的二阶纯准P波控制方程;Zhan等[9]提出旋转波数的概念,科学地将VTI介质解耦波动方程旋转到了TTI介质中,并且推演出TTI介质下的纯P波方程形式,利用伪谱法和有限差分法联合求解了该波动方程;Zhang等[10]在Xu等[19]的基础上,通过提出新的旋转方式推导出TTI介质三维二阶纯准P波方程,该方程相比较Zhan等[9]的方程,不存在伪微分算子,且结构简单,便于利用有限差分法快速求解。
本文以Zhang等[10]的研究成果为基础,通过引入辅助波场推导出TTI介质纯准P波一阶压力-速度方程;利用旋转交错网格技术实现了数值模拟;并且引入了完全匹配层(Perfectly Matched Layers,PML)吸收边界条件处理人工边界问题。
1 TTI介质二阶纯准P波方程的建立
Xu[20]根据Alkhalifah[11]所提出的声学假设下VTI介质频散关系,通过引入椭圆微分辅助算子R,推导并改进了VTI介质中的纯准P波方程:
式中椭圆微分辅助算子
二阶偏导数
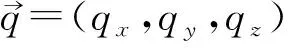
TTI介质可以认为是VTI介质的一般形式,可以通过投影变换将VTI介质转换为TTI介质。故要得到TTI介质下的纯准P波方程,可将传播方向从原始坐标系(XYZ)进行两次旋转变换投影到TTI介质本构坐标系(X′Y′Z′)中,设第一次旋转产生的过渡坐标系为(X0Y0Z0)。图1给出了两次坐标系旋转之间相互关系。

图1 坐标系空间关系示意图Figure 1 A schematic diagram of coordinate system spatial relation

(2)
第二次坐标系旋转,将(X0Y0Z0)坐标系以Z0轴为对称轴逆时针旋转φ角度,得到(X′Y′Z′)坐标系。对应的旋转矩阵为:
(3)
将两次旋转过程合并为一个旋转关系:

(4)
进而得到波场传播方向向量的坐标转换关系:
(5)
接下来求取TTI介质本构坐标系(X′Y′Z′)下波场传播的方向向量表达式。根据式(1)可以很容易得到该坐标系下TTI介质纯准P波方程形式:
(6)

(7)

将式(5)代入式(7)并对其作傅里叶逆变换至时间-空间域,即可得到TTI介质纯准P波二阶方程:
+C5uxy+C6uyz)
(8)
式中R的求取同式(6);系数Ci如下:
2 TTI介质纯准P波一阶压力-速度方程的建立及求解方法
2.1 方程的建立
TTI介质纯准P波一阶压力-速度方程方程的推导采用类似各向同性介质中二阶声波方程降阶的方法。首先引入辅助波场p、vx、vy、vz,设:
(9)
将式(9)带入式(8)可以得到TTI介质纯准P波一阶压力-速度方程组:
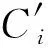
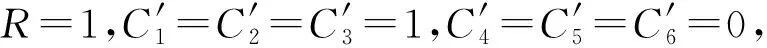
2.2 数值求解方法
对于本文建立的一阶压力-速度方程,可以采用旋转交错网格[22]高阶有限差分方法来求解。旋转交错网格发展于交错网格[23-25]的基础之上,它通过网格旋转差分求解TTI介质中的地震波方程,避免了常规网格差分求解中的插值和拟合问题[26]。旋转交错网格有限差分具体实现过程[22]是:首先计算出沿对角线方向的波场差分值,然后用这些对角线方向差分的线性组合求解出沿坐标轴的差分数值,其网格剖分方法如图2所示。
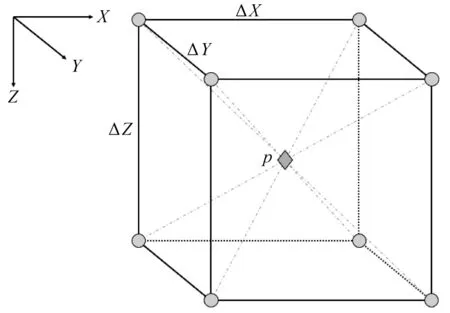
图2 三维旋转交错网格示意图Figure 2 A schematic diagram of 3D rotating staggered grid
(11)

(12)
式中en为差分系数,可通过Taylor展开求解[27],其同阶具体数值与交错网格[28]相同。经过线性迭代组合便可得到沿坐标轴方向的旋转交错网格差分算子计算公式:
(13)
2.3 人工边界条件
边界条件是地震波动方程求解的重要研究内容[23-24,29-30],本文应用PML吸收边界条件处理人工边界问题。依据完全匹配层的分裂思路[29],在式(10)中引入沿x、y、z方向的边界衰减因子dx(x)、dy(y)、dz(z),以p分量为例,给出了TTI介质纯准P波一阶压力-速度方程的PML吸收边界条件:
(14)
3 数值模拟
由于考虑到计算效率,本文将在二维情况下对上述纯准P波一阶压力-速度方程及其他学者给出的方程进行数值模拟,并对数值模拟结果进行对比分析。
3.1 均匀TTI介质模型
给定一个单层均匀的TTI介质模型,模型参数见表1;其网格尺寸4 000 m×4 000 m,空间步长Δx=Δz=10 m,时间采样步长Δt=1 ms;激发震源选用Ricker子波置于介质中心,主频16Hz。对上述模型分别采用Zhang提出的纯准P波二阶方程[8]及本文提出的纯准P波一阶压力-速度方程进行数值模拟,获得0.6s的波前快照对比如图3所示。

表1 均匀TTI介质模型参数
由图3可知两种方程的波前快照传播规律相同,但纯准P波一阶压力-速度方程的计算精度略高于纯准P波二阶方程;此外,PML边界在两种方程下都能够很好地吸收能量,解决人工边界问题。在相同条件下,一阶方程计算效率明显高于二阶方程:二阶方程耗时344s,而一阶方程只耗时190s。
3.2 水平层状模型
给定一个两层水平层状模型,其中第一层为各向同性介质,第二层为TTI介质。模型参数见表2;模型尺寸规模为2 000 m×2 000 m,空间步长Δx=Δz=5 m,时间采样步长Δt=0.2ms;震源同样选用Ricker子波,主频24.0Hz,并置于(1 000m,0m)处;接收点位于地表,界面位于模型中间,记录时间层数为4 000,400道接收。对上述模型分别采用Zhou提出的二阶耦合准P波方程[5]及本文提出的纯准P波一阶压力-速度方程进行数值模拟,对比如图4所示。

表2 水平层状介质模型参数
由图4可知,本文给出的纯准P波一阶压力-速度方程没有伪横波噪音干扰,而二阶耦合准P方程在模拟TTI介质中地震波传播的过程中存在图4(a)所示的低频低速的伪横波。这种不可消除的波型在逆时偏移时会产生成像假象,从而影响我们对地层结构的判断。

(a)纯准P波二阶方程;(b)纯准P波一阶压力-速度方程图3 均匀TTI介质波前快照对比Figure 3 Homogeneous TTI medium wavefront snapshots comparison
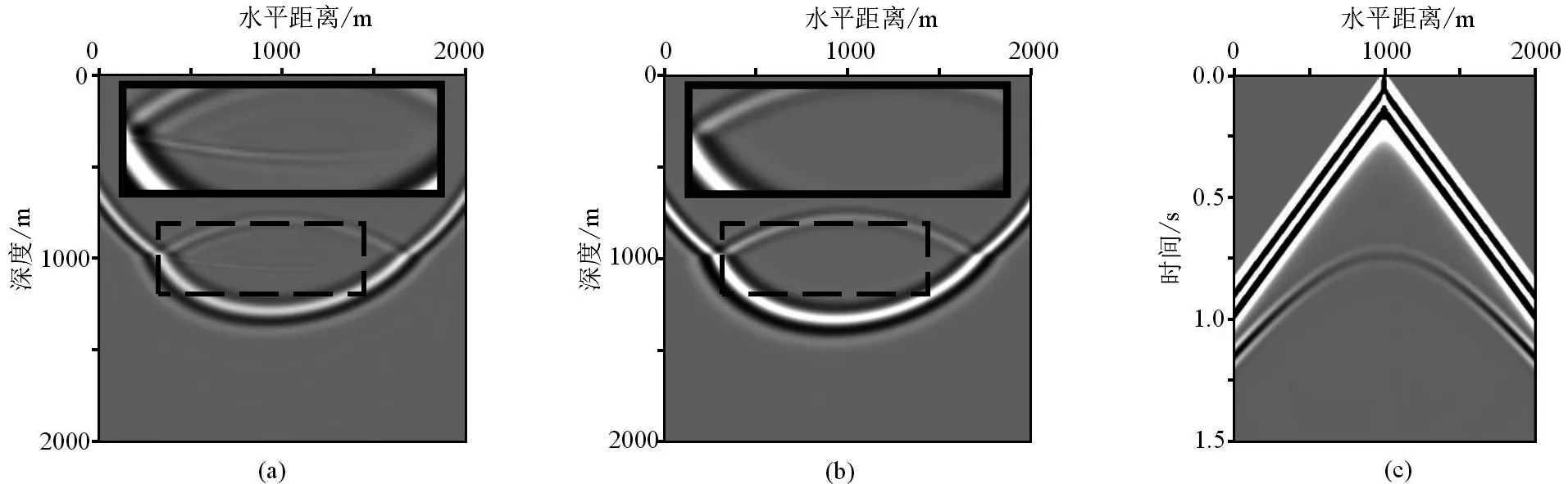
(a)二阶耦合准P波方程波前快照;(b)纯准P波一阶压力-速度方程波前快照;(c)纯准P波一阶压力-速度方程单炮地震记录图4 水平层状介质波前快照和单炮地震记录Figure 4 Horizontal layered medium wavefront snapshot and single-shot seismic record
3.3 TTI介质Wedge模型试算
通过均匀TTI介质模型试算,可知本文推导的纯准P波一阶压力-速度方程与二阶形式方程的数值模拟结果在计算精度上并无明显区别,但计算效率更高。但当模型对称轴方向变化较为剧烈时,是否会产生不稳定问题,并不能获得很好的验证。
为说明该问题,本文给出了一个TTI介质楔形模型。模型尺寸为3 000 m×3 000 m;空间步长Δx=Δz=10 m,时间采样步长Δt=0.5 ms空间采样间隔为10m;震源为Ricker子波,主频15Hz,埋深10m;检波器位于地表300道接收;模型介质参数如图5、图6所示。对上述模型分别采用Zhou提出的二阶耦合准P波方程[5]及本文提出的纯准P波一阶压力-速度方程进行数值模拟。
纯准P波一阶压力-速度方程数值模拟结果如图7所示;二阶耦合准P波方程数值模拟结果如图8所示。由波场快照结果对比可知:论文推导的一阶纯准P波方程,在各向异性对称轴角度变化幅度最大的地方,波场并没有发生不稳定的现象,仍然能够在介质中保持稳定传播;而二阶耦合准P波方程,在t>1.5s时,已经出现了不稳定现象。超过3.5s后,结果已经基本无法显示。
4 结论
①推导了TTI介质纯准P波一阶压力-速度方程,并给出了数值求解的方法。相比纯准P波二阶方程,本文给出的方程在计算精度相同的情况下,具有更高的计算效率;
②本文给出的一阶方程可以更好地适用PML吸收边界条件,同时能够结合旋转交错网格技术,避免了进行各向异性介质数值模拟时由于网格剖分产生的特殊误差,提高了数值模拟结果的精度;
③设计了楔形TTI介质模型, 验证了本文的方程能够稳定地模拟对称轴参数变化剧烈的情况。由此可认为该纯准P波方程对于改善各向异性逆时偏移成像的质量以及提高计算效率有一定推动作用。

(a)纵波速度Vp0;(b)极化角θ图5 楔形模型速度和角度参数Figure 5 Wedge model velocity and angle parameters

(a)Thomsen参数δ;(b) Thomsen参数ε图6 楔形模型各向异性参数Figure 6 Wedge model anisotropic parameters

(a)t=1.6s时刻波前快照;(b)单炮地震记录图7 纯准P波一阶压力-速度方程数值模拟结果Figure 7 Pure quasi-P wave first-order pressure-velocity equation numerical simulation results
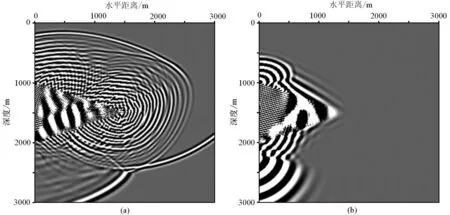
(a)t=1.6s时刻波前快照;(b)t=3.6s时刻波前快照图8 二阶耦合准P波方程数值模拟结果Figure 8 Second-order coupled quasi-P wave equation numerical simulation results
