基于UML的对称一元关联研究
2018-08-24杨卓卿
杨卓卿
(重庆邮电大学软件工程学院,重庆400065)
0 引言
在软件开发领域,统一建模语言(Unified Modeling Language,UML)被广泛认为是一种标准化的、通用的面向对象建模语言。尽管如此,UML对客观世界的描述能力有限,某些常见的语义,在UML中还没有足够的元模型来解释[1]。
关联的概念是大多数建模语言的一个关键元素,在概念模型甚至是程序代码中,关联定义了类之间的关系。在对客观世界进行建模时,最常见的是二元关联,即维系两个类的关联,此外,一元关联也不可忽视,顾名思义,一元关联只涉及一个类,也叫自关联。在现实生活中,普遍存在一种特殊的一元关联,其特点是关联双方所扮演的角色是对等的。例如,人与人之间互为邻居的关系、一个数学函数与它的反函数存在互为反函数的关系等,这种关联叫做对称一元关联[2]。然而,主流的建模语言UML缺少对称一元关联语义的支持。
对此,本文首先分析了对称一元关联的语义,根据语义抽象出了对称一元关联的集合、图等数学模型,再结合数学模型和UML类图元模型,分析了UML无法支持对称一元关联的原因,以及由此引发的代码生成问题。然后讨论了对称一元关联的数据结构,提出通过扩展UML类图元模型使UML支持对称一元关联建模的方法,并针对每种数据结构给出代码生成算法,最后通过实际例子的应用验证了该方法的可用性和有效性。
1 背景知识
模型驱动架构(Model Driven Architecture,MDA)是对象管理组织(Object Management Group,OMG)提出的一个软件开发方法。所谓模型驱动,就是一种用模型来指导软件工程师对软件系统的理解、设计、构造、部署、操作、维护和改进的方法[3]。
为了描述元建模的机制和方法,OMG定义了MDA的四层元模型体系结构[4],分别是M0层、M1层、M2层、M3层。M0层是信息层,也叫客观世界;M1层是模型层,用于描述M0层的信息;M2层是元模型层,用于描述M1层的模型;M3层是元元模型层,其元素提供了定义元模型的基本结构。从M0层到M3层是一个逐层抽象的过程。
在MDA中,不同的应用场景建立不同的模型,不同的模型由不同的元模型来描述。类图元模型是描述类图的模型,其作用是为类图的建立定义一系列建模元素,称之为类图元模型中的“元元素”。在类图元模型中,用一个名为“Association”的元元素来描述类图中的“关联”。类图中的“关联”都是类图元模型中的“Association”元元素实例化后的对象。
UML标准文档中对关联的定义是“一种在类型化实例之间发生的语义关系”[5]。一个关联至少有两个端点,称为关联端[1],关联端的名称称为角色,每一端与该关联涉及的一个类相连接。关联端的多重性表示关联的某一端所连接的类对象的数量,多重性的值可以是一个特定的值,也可以是一个整数区间。关联端可以是可导航的或不可导航的,可导航端所连接的类的对象将隐式地成为另一端所连接的类的成员属性,称为伪属性[6]。单向关联的关联端的其中一端是可导航的,双向关联的两个关联端都是可导航的[7]。
2 对称一元关联的研究
本节将讨论对称一元关联存在的问题及其语义,然后讨论实现对称一元关联的数据结构,就存在问题提出了扩展UML类图元模型的方法和代码生成算法。
2.1 存在问题
对称一元关联在现实生活中普遍存在,文献[2]中使用的概念建模语言(Conceptual Modelling Language,ConML[8])提供了对称一元关联的建模所需的元模型和图形符号,但是,UML作为一套被软件开发人员广泛使用的建模语言,其元模型并不支持对称一元关联的建模。
在理论上,如果用UML类图表示对称一元关联,不仅关联两端连接到同一个类,而且其关联两端的角色名、多重性、可导航性完全相同。以人与人之间的邻居关系为例,每一个人都可以有多个邻居,且邻居的关系是相互的、对等的,在一个邻居关系中,每一方都是另一方的邻居。图1(a)是用UML类图表示的邻居关联。然而这将会与UML的建模规则产生矛盾。
图1(c)是UML中关联的元模型,用其表示“邻居”关联得到的对象图如图1(b)所示。图1(b)中的对象图出现了两个完全相同的“neighbour”对象,然而在UML的标准文档中,NamedElement元元素定义了一个名为isDistinguishableFrom()的方法来判断UML模型中的两个命名元素是否可以在同一个命名空间中逻辑共存[9],当两个命名元素是不同类型的,或者同类型不同名时,两者可以同时存在于同一个命名空间中。
类图中的关联端的角色是由Property元元素实例化而来的,而Property元元素间接继承了NamedElement元元素,因此关联端的角色也遵循isDistinguishableFrom()方法的规则。可见,图1(b)中的两个相同的neighbour对象不能同时存在。
由对称一元关联的UML建模问题,衍生出的是其代码生成问题。对称一元关联两端的角色既是相同类型的,又有相同的名称和可导航性。在生成数据访问代码时,会导致语义的缺失,从而生成错误的代码。以“邻居”关联为例,如果按照UML现有的语义、约束和代码生成规则,在将类图生成实体类代码时,Person实体类代码中会出现两个同是Person类型且同样名为neighbour的成员变量,其Java代码如下。显然这样的代码无法通过编译。
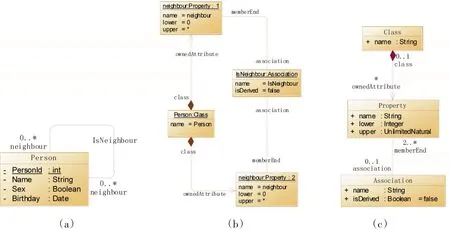
图1 用UML中关联的元模型表示“邻居”关联

2.2 对称一元关联的语义
为了解决对称一元关联无法使用UML建模的问题,下面将从对称一元关联的语义着手,通过数学方法分析产生问题的原因。
在UML中,类是由一组拥有相同特征的对象组成的集合,这些对象描述了客观世界中的真实个体;关联是两个类对象之间的二元关系,描述的是客观世界中的个体之间的联系。从数学集合的角度看,如果将类看成集合,将类对象看成集合中的元素,那么关联就是两个集合的元素之间的二元组。由于这些二元组描述的是同一类的二元关系,因此它们也组成了关联的集合。
在邻居关联中,将Person、neighbour都看作集合,用p表示Person集合中的元素,用pn1表示Person集合中扮演neighbour角色的元素,pn2表示Person集合中另一个扮演neighbour角色的元素,则Person集合可以表示为公式(1)。
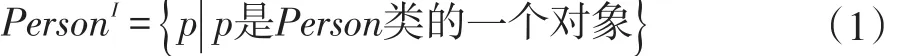
IsNeighbour关系中只存在neighbour一个角色。neighbour集合中的元素都是Person集合中的一个元素与Person集合中的另一个元素组合成的二元组,表示为公式(2)。
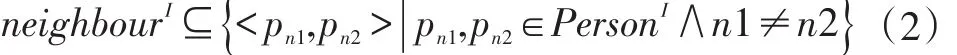
公式(2)表示的 neighbour集合中,二元组<pn1,pn2>表示pn2在当前关联中所扮演的角色是neighbour,从相反的导航方向来看,pn1在当前关联中所扮演的角色也是 neighbour,因此<pn1,pn2>与<pn2,pn1>等价,也就是说二元关系neighbour与其自身的逆等价,表示为公式(3)。
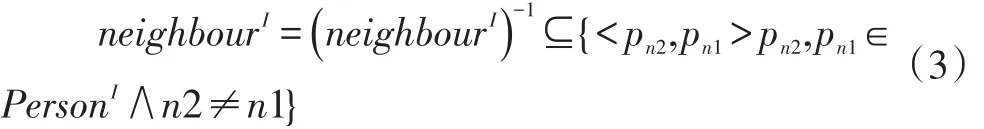
如果把Person集合中的每个元素看成顶点,把元素之间的关系看成顶点与顶点之间的边,把Person集合中的每个元素看成顶点与顶点之间的关联函数,就可以将对称一元关联转化为图,如图2所示。根据关联“IsNeighbour”的语义,由于对称一元关联具有对等性和相互性,因此该图是一个无向图[10]。
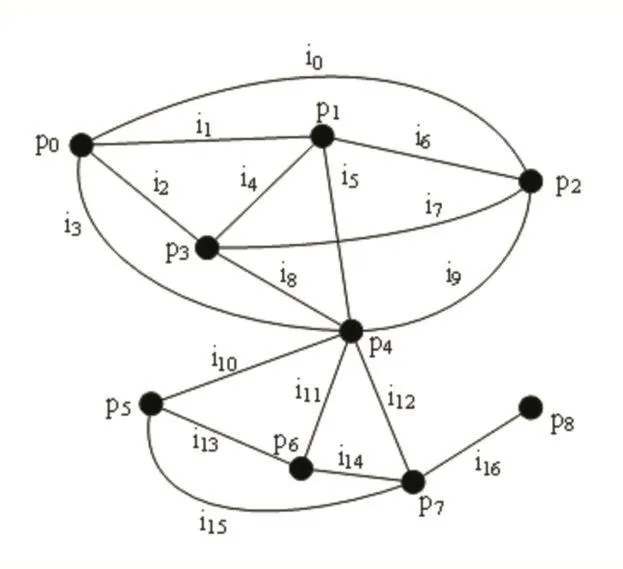
图2 用图表示“邻居”关系
其中,pn(n=0,1,2,3,4,5,6,7,8)是Person集合中的元素,其中 p0、p1、p2、p3、p4两两之间互为邻居,p4、p5、p6、p7两两之间互为邻居,p7和 p8互为邻居。如果用G表示这个图,用V(G)表示图G中的所有顶点的集合,用E(G)表示图G中的顶点之间边的集合,用φ(G)表示顶点与顶点之间的关联函数,则该图记为:
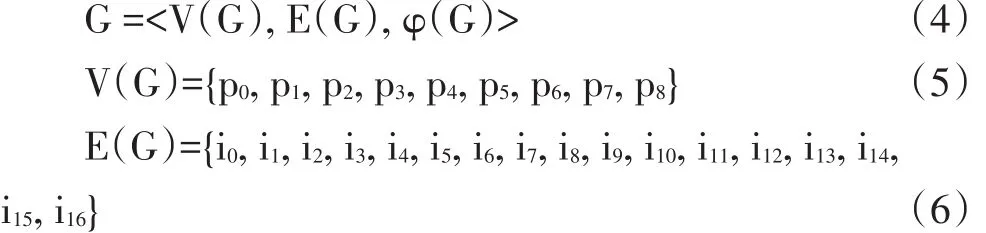
φ(G)=E→V×V,且φ(i0)=(p0,p2),φ(i1)=(p0,p1),φ(i2)=(p0,p3)
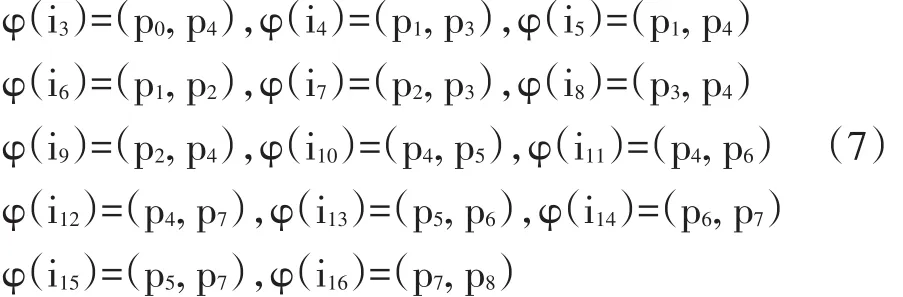
综上所述,对称一元关联的特点是关联双方所扮演的角色是相同的且具有相互性。正是由于这个特点,当用UML表示对称一元关联时,无法区分两个相同的角色。对此,可以对UML元模型进行扩展,使之支持对称一元关联的建模。
2.3 实现对称一元关联的数据结构
对称一元关联语义的特殊性导致了在生成代码时出现错误代码,下面将分析实现对称一元关联的几种数据结构,为生成实体类代码提供基础。
根据上一节所讨论的语义,可以将现实生活中的对称一元关联抽象成一个无向图。一个图所包含的信息由两个方面,一是图中顶点的信息,二是顶点与顶点之间关系的信息,即边的信息。无论采用什么数据结构来存储图,都要完整、准确地反映这两方面的信息[11]。除了文献[2]中使用的集合类型以外,常用的存储无向图的数据结构有邻接矩阵、邻接表、邻接多重表。
(1)邻接矩阵
邻接矩阵存储图的方法是用一个一维数组存放图中的顶点的信息,用一个二维数组存放图中边的信息,这个二维数组也称为邻接矩阵。如图2的无向图有九个顶点,则一维数组的长度为9,如公式(8)所示,其邻接矩阵是一个9×9的方阵,由于该图是一个无环无向图,所以方阵中主对角线上的各个位置的值都为0,其余位置的值根据两个顶点之间是否有边而定,若有边则值为1,若无边则为0,如公式(9)所示。
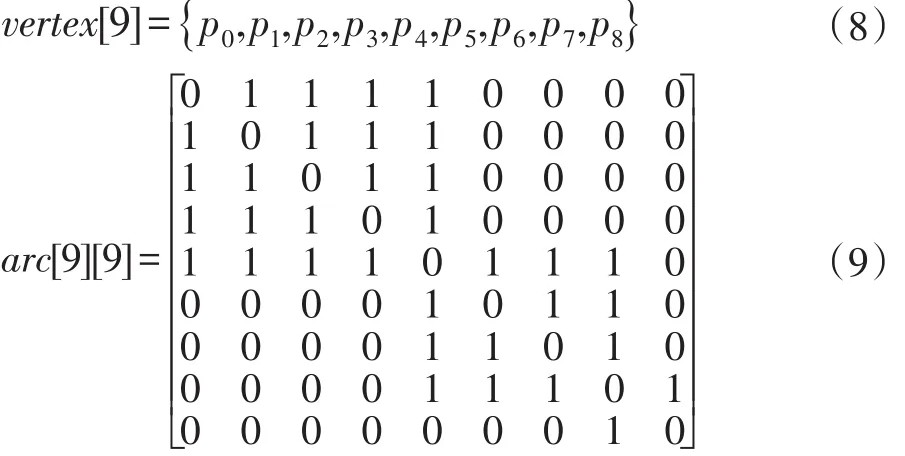
从公式(9)中不难看出,在 p0、p1、p2、p3、p4五个顶点构成的五阶子式中,每两个不同顶点之间的边的信息都被重复存储了一次,p4、p5、p6、p7四个顶点构成的四阶子式和p7、p8两个顶点构成的二阶子式同理,而根据对称一元关联的语义,被重复存储的两个边并无区别,只需存储一次,因此会出现数据的冗余。
(2)邻接表
邻接表存储图的方法是将每个顶点的所有邻接点链接成一个单链表,称为顶点的边表。图2的无向图的邻接表存储示意图如图3所示。
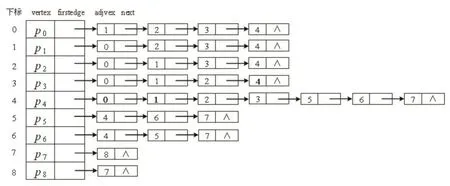
图3 图2的无向图的邻接表存储示意图
从图3中可以看出,邻接表与邻接矩阵一样,也会出现两个不同顶点之间的边的信息被重复存储的情况。
(3)邻接多重表
邻接多重表主要用于存储无向图,其存储图的方法与邻接表类似,但在邻接表的基础上针对无向图的边重复存储的问题做了改进。图2的无向图的部分顶点的邻接多重表存储示意图如图4所示。
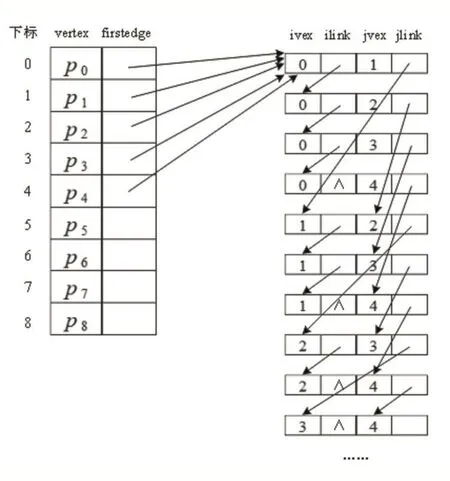
图4 图2的无向图的邻接多重表存储示意图
从图4中可以看出,两个不同顶点之间的边的信息只存储了一次,便于边的查找和删除。
邻接矩阵便于确定两个顶点之间是否有边,但时间代价较高,在存储无向边时存在边信息的冗余,在处理稠密图时,空间效率较高。邻接表的时间代价较低,但在存储无向边时同样存在边信息的冗余,在处理稀疏图时,空间效率较高。邻接多重表的时间代价较低,便于边的查找和删除,在存储无向边时不存在边信息的冗余,但是其结构比前两种复杂,适用于查找和删除操作较频繁的无向图。表1对比了这三种图的数据结构的优缺点。
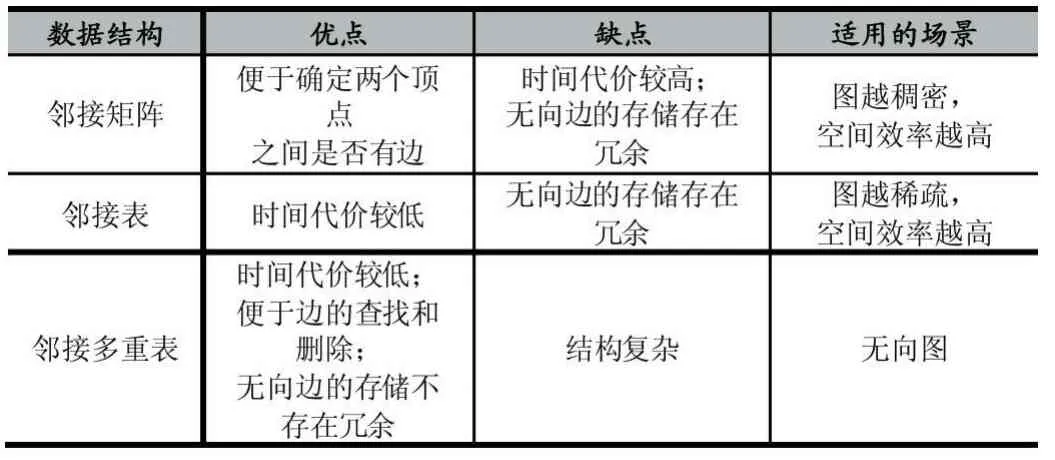
表1 邻接矩阵、邻接表、邻接多重表的对比
无向图的邻接矩阵、邻接表、邻接多重表的存储各有利弊,在具体实现时,不但要根据图的稀疏和稠密程度选择合适的存储方式,而且要考虑待解决问题的特殊需求。
2.4 扩展UML类图的元模型
通过前文的讨论可知,UML元模型不支持对称一元关联的语义表示,需要对UML元模型进行扩展。本节将讨论通过扩展类图元模型的元属性和约束使UML支持对称一元关联建模的方法。
对象约束语言(Object Constraint Language,OCL)是一种用于描述UML模型约束的形式化语言[12],与传统形式化语言相比,对象约束语言具有良好的易读性、易写性和易理解性。本文通过为Association元元素添加元属性和为Property添加对象约束的方法[13],对类图元模型进行扩展,使之支持对称一元关联的语义。首先,为了标识模型中关联是否是对称一元关联,在UML标准的基础上,扩展UML类图元模型中的Association元元素,在Association元元素中添加一个元属性,该元属性的信息如表2。
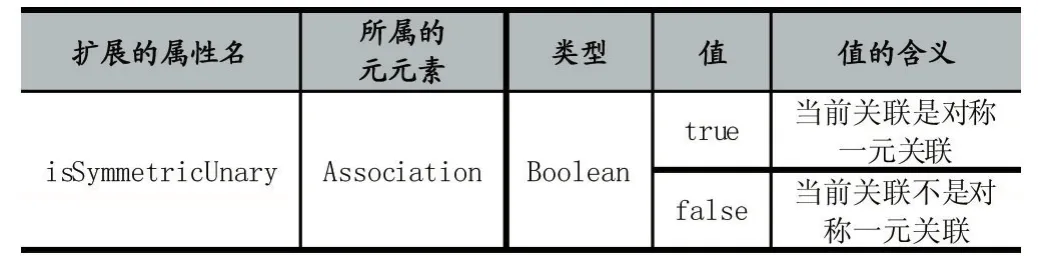
表2 扩展的isSymmetricUnary属性的信息
由于对称一元关联的建模问题源于关联两端的角色,而关联端的角色是Property元元素的实例对象,因此须在Property元元素中对Association元元素的is-SymmetricUnary元属性添加约束,用OCL描述该约束如下。

上述约束是对Property元元素的对象的约束,首先判断当前Property对象所在的关联是否有两个关联端,如果是,则定义一个名为otherEnd的变量,用来表示关联的另一端,然后给关联的isSymmetricUnary属性赋值。如果两个关联端的名称、数据类型(即关联两端所连接的类)、可导航性、多重性的上界和下届之中有一项不同,则isSymmetricUnary属性的值为false,否则isSymmetricUnary属性的值为true。在建模时,计算机根据该约束自动判断关联的类型并给isSymmetricU-nary属性赋值。
此外,在UML中,Property元元素间接继承了NamedElement元元素,子类可以根据需要重写父类的方法,因此可以在Property元元素中重写NamedElement元元素的isDistinguishableFrom()方法,用于约束对称一元关联中的角色共存。当Association元元素的is-SymmetricUnary元属性值为true时,关联两端相同的角色可以在当前命名空间中逻辑共存。用OCL描述重写的isDistinguishableFrom()方法如下。

上述方法同样是对Property元元素的对象的约束,在NamedElement元元素的isDistinguishableFrom()方法的基础上,添加了处理对称一元关联的两个相同关联端的共存问题的分支,当Property对象所在的关联的isSymmetricUnary属性值为true时,关联两端相同的角色可以在当前命名空间中逻辑共存。对于非对称一元关联的情况,若两个关联端具有相同的类型,则二者是否可以共存取决于二者的名称是否相同:如果名称相同,则二者不可以共存,否则可以共存;若两个关联端具有不同的类型,则二者可以共存。
为了方便建模人员在建模时根据需求为对称一元关联选定合适的实现方式,可以在类图元模型的Association元元素中标记对称一元关联的实现方式,在生成代码时,根据不同的标记值生成不同的代码。首先定义要扩展的元属性的枚举值,在UML标准的基础上,在类图元模型中添加一个名为“SUAImplementation”的枚举型数据类型,这个数据类型的值有“CollectionType”、“AdjacencyMatrix”、“AdjacencyList”、“AdjacencyMultiList”,分别表示集合类型、邻接矩阵、邻接表、邻接多重表;然后在类图元模型的Association元元素中添加一个元属性,该元属性的信息如表3。

表3 扩展的implementation属性的信息
需要注意的是,只有当isSymmetricUnary元属性的值是true时,implementation元属性才会启用,否则其值为空。
图5展示了扩展后的UML类图元模型。
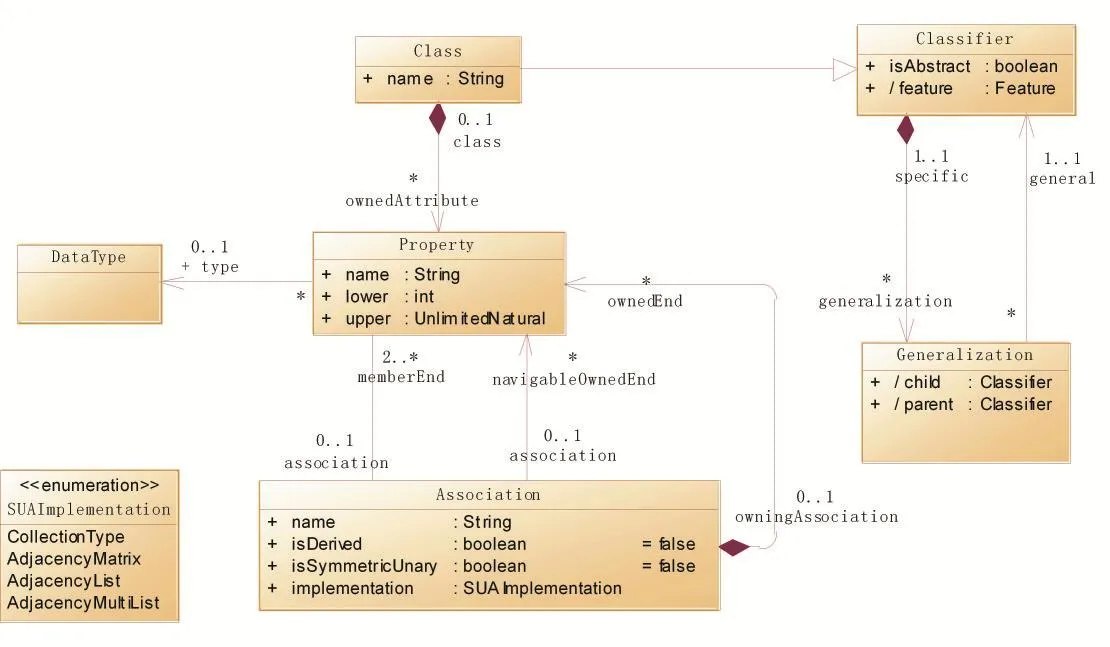
图5 扩展UML类图元模型
通过扩展Association元元素的元属性以及Property元元素的约束,从元模型层面使UML支持对称一元关联的语义,为建模工具实现对称一元关联的建模提供了理论基础。
2.5 代码生成算法
从模型生成代码是MDA思想中模型驱动开发的重要过程。在应用程序的三层架构中,领域对象作为数据的载体,扮演着关键的角色,领域对象是实体类的实例,因此实体类的代码生成尤为重要。常用的代码生成方法是基于模板的代码生成方法。使用模板的好处是模板与数据分离,当需要改动代码时,只需修改模板,易于复用[14]。模板中可变的部分需要用模型的信息进行替换,不可变的部分则是代码中固定不变的语法格式。
除了文献[2]中给出的代码生成方法,本文的2.3节还讨论了三种实现对称一元关联的数据结构,下面将给出这些实现方式的代码生成算法,其中被“%”包裹的部分为需替换成元模型的元元素中的元属性的值。
对称一元关联实体类代码生成算法
输入:UML类图的模型信息
输出:对称一元关联实体类代码


上述代码首先获取当前类图的模型信息,循环判断模型中的每个关联,如果关联满足对称一元关联的条件,则按照实体类代码的模板框架生成类的定义代码,先在类中循环生成该类的成员属性,然后判断implementation属性的值,生成该值所标识的数据结构的代码。
3 应用
邻里社交平台是一个专门为促进小区内邻居之间的交流而开发的平台,居民在该平台上可以随时查看生活圈,关注邻居的最新动态,还可以向邻居发出帮助请求,同时也可以帮助邻居解决生活上遇到的难题,满足了邻里之间的交流与沟通的需求。
本节将以邻里社交平台的开发为例,采用本文提出的方法,使用PowerDesigner实现对称一元关联的建模和代码生成,验证本文研究的方法在实际软件开发过程中的可用性和有效性。
3.1 对称一元关联的应用
本节讨论对称一元关联的应用,以“邻居”关系为示例,建立了对称一元关联的UML类图,然后在PowerDesigner中实现对称一元关联数据结构的选择,然后根据上一节提出的算法生成代码。其次,还将同样的方法应用到一般的关联中,说明方法的通用性。
(1)建立对称一元关联的领域模型
邻里社交平台的主要业务是实现邻居之间的信息共享和交流。其中的特殊点在于,“邻居”关系属于对称一元关联,在使用类图建立领域模型时,需用到本文提出的对称一元关联的建模方法。其领域模型如图6所示。
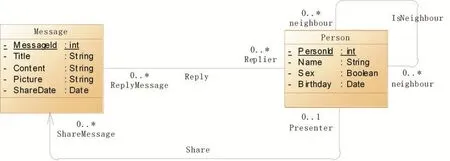
图6 邻里社交平台核心业务的领域模型
领域模型中Person类表示使用系统的用户,用户与用户之间的邻居关系通过名为“IsNeighbour”的关联来表示,该关联双方的邻居角色用名为neighbour的角色表示,且多重性的值为0...*,两端都是可导航端。根据前文中提出的UML元模型的扩展约束,该领域模型中IsNeighbour关联满足对称一元关联的条件,因此该关联的isSymmetricUnary属性值为true,进而关联两端相同的neighbour角色可以在当前命名空间中逻辑共存。
(2)数据结构的选择和代码生成
为了方便建模人员在生成代码时选择合适的数据结构,使用PowerDesigner提供的Profile扩展功能,在资源编辑器中将一个用于标识对称一元关联实现方式的扩展属性添加到类图的Association元元素下,并给定这个扩展属性的四个可选值,分别表示使用集合类型、邻接矩阵、邻接表、邻接多重表,然后将四种实现方式的代码生成算法应用到这个扩展属性中,最后提供建模人员的操作界面,如图7所示。
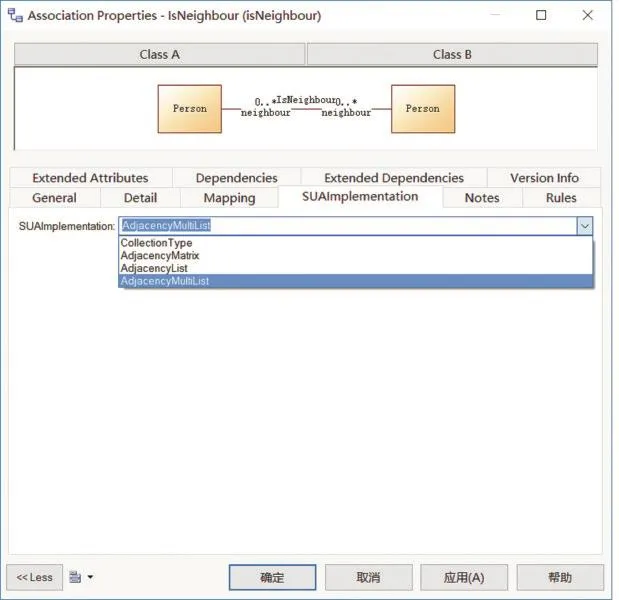
图7 在PowerDesigner中选择代码生成的方式
通过扩展PowerDesigner的操作界面,建模人员在建模时可以在类图的Association元素的Properties窗口下选择合适的数据结构以标记使用哪种方式来生成对称一元关联的代码。当然,这四个选项可用的前提是当前的关联满足对称一元关联的条件。如图7所示,此处选择邻接多重表来实现“邻居”对称一元关联,生成的Java代码如下。


3.2 其他关联的应用
在图6所示的领域模型中,Reply关联描述了用户与消息之间的“回复”关系,一个用户可以回复多条消息,一条消息可以被多个用户回复。用户的角色用名为Replier的角色表示,消息的角色用名为ReplyMessage的角色表示,关联两端的多重性的值都为0...*且都为不可导航端。
虽然Reply关联两端的角色的多重性、可导航性相同,但类型、角色名都不相同,不满足对称一元关联的条件,因此该关联的isSymmetricUnary属性值为假,关联两端的角色可以在当前命名空间中逻辑共存。在本文的讨论范围内,对于非对称一元关联,无法选择对称一元关联的实现方式,SUAImplementation属性被禁用,如图8所示。
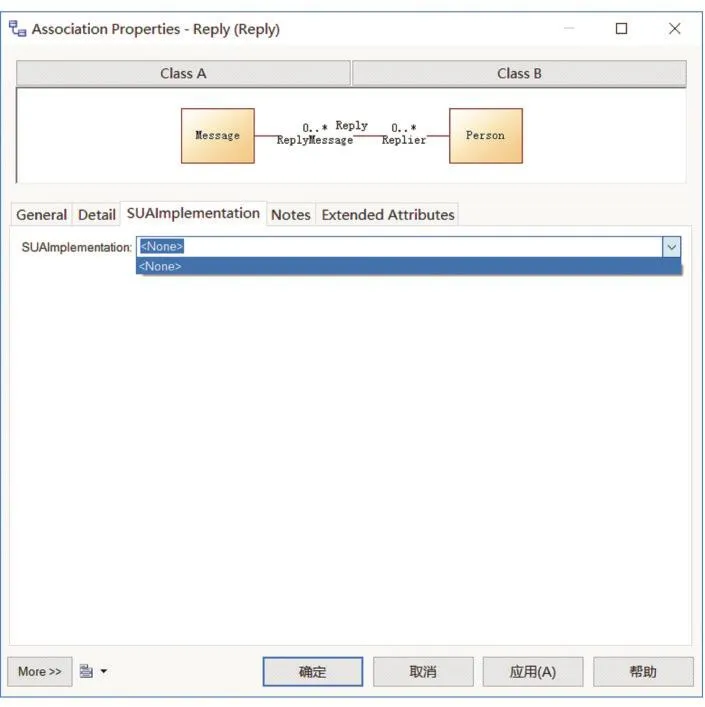
图8 “Reply”关联的SUAImplementation属性被禁用
因为Reply关联不属于对称一元关联,所以在生成代码时使用的是传统的代码生成的算法,将Replier角色作为成员属性生成到Message类中,将ReplyMessage角色作为成员属性生成到Person类中,由于两端的多重性值都为0...*,所以数据类型为数组,生成的Java代码如下。


4 相关工作
文献[15]针对UML存在组合关联语义定义模糊,导致从领域模型自动转换为数据访问层代码的精确度不足的问题,提出了描述逻辑CATSbqr语言,并准确地描述了UML组合关联的语义以及动态操作复杂对象数据的语义,并通过实例说明了该方法的实用性,为实现领域模型到数据访问层的代码自动化提供了理论基础。
文献[2]针对UML无法表示对称一元关联的问题,提出使用ConML元模型中的半关联(SemiAssociation)元元素,将对称一元关联分解成一个主半关联(Primary)和一个次半关联(Secondary),且允许关联两端的角色相同,并使用Microsoft Visual Studio Enterprise 2015、Visual Paradigm 14.0、ArgoUML 0.34和 XCode 8.0这四种代码生成工具生成对称一元关联模型的代码,通过表达语义的精确与否、是否有冗余、是否能编译、是否无需开发者编辑等指标对比四种工具生成代码的质量,得出的结论是为了能生成满足对称一元关联语义的代码,最优的解决方案是修改底层元模型和代码生成规则,将这些规则运用到代码生成工具中,从而实现对称一元关联。
与上述关于UML关联的研究工作相比,本文针对客观世界普遍存在但UML无法支持的对称一元关联进行了重点讨论,用集合、图等数学方法分析了对称一元关联的语义,通过扩展UML类图元模型实现语义的支持,并讨论了对称一元关联的数据结构和代码生成算法,提高了UML的建模能力,并且实现根据需求生成更高效、更少错误的数据访问代码。
5 结语
UML元模型定义了模型元素在同一个命名空间中共存的约束,使UML类图元模型无法表示对称一元关联的语义。由于对称一元关联的特殊语义,在从类图生成代码时,会导致语义的缺失,从而生成错误的代码。本文针对以上两个问题,使用集合、图等数学方法分析了对称一元关联的语义,讨论了集合、邻接矩阵、邻接表、邻接多重表四种可用于对称一元关联的数据结构,提出了通过扩展UML类图元模型使UML支持对称一元关联建模的方法和代码生成算法,最后通过实际例子的应用验证了该方法的可用性和有效性,为实现对称一元关联的建模及数据访问代码的自动化提供了理论基础。
