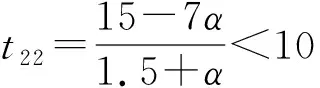考虑双退货期限的在线零售商退货策略研究
2018-08-23何啸源甄学平
何啸源 甄学平 刘 斌
(上海海事大学 经济与管理学院,上海 201306)
1 模型构建
1.1 问题描述
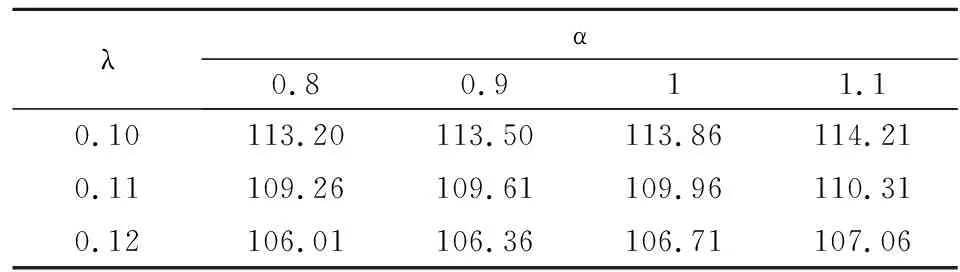
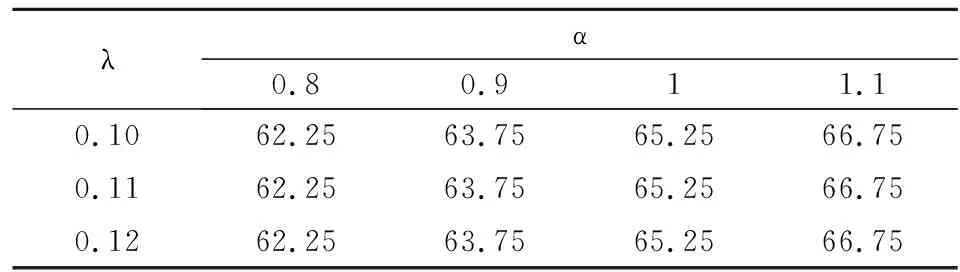
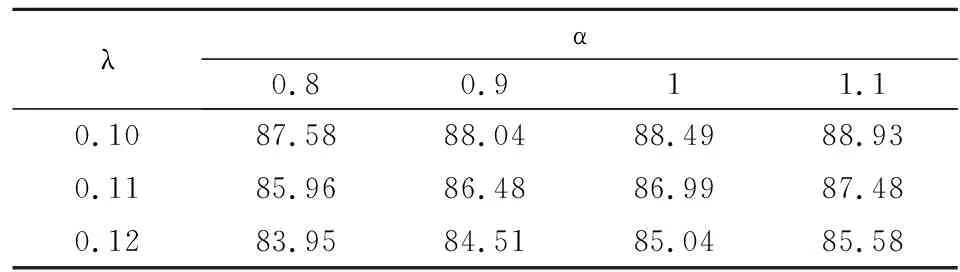
本文研究的是只有一个制造商和一个零售商的两级供应链。在销售季节的开始,制造商以批发价格w销售给在线零售商,然后在线零售商决定订购数量Q并以价格p出售商品。消费者购买后,在线零售商为消费者提供总时长为t1+t2的退货选项。在退货期限t1内,零售商全额退款,出于实际的退货选项。在退货期限t1内,零售商全额退款,出于实际和运算优化的考量,t1为固定参数。超过退货期限t1,在线零售商提供部分退款为r的退货政策,t2是部分退款期限。考虑到退货期限,消费者可以获得一个额外的体验价值at,a是消费者体验价值参数。消费者根据对商品的估值v和体验价值at决定是否保留产品。由于全额退款退货期限t1较短,本文假设此时退货商品的价值基本不受影响,和所有未销售商品的残值同为s。而超过全额退款退货期限t1的退货商品的残值为s1,s1=s-kt2,k是产品价值衰减参数.出于实际的考虑,现实中想要退货的消费者由于某些原因而未能够在规定的退货期限内完成退货。所以,根据Hess和Mayhew的相关研究,假设退货成功率为H(t)=1-e(-λt),且在λt相对0 表1 符号说明 消费者收货使用后,在全额退款期限t1内,衡量对产品的估值v和体验价值αt1与全额退款p的大小选择是否退货,即当v+αt1≥p时,选择保留产品,反之则选择退货。在退货期限t1内,想要退货消费者的退货成功率为λt1。当想要退货的消费者未能成功退货时,在部分退款期限t2内,这部分消费者通过比较对产品的估值v和体验价值(αt1+αt2)与部分退款r的大小,重新考虑是否退货。当对产品的估值加上体验价值大于退款时,即v+αt1+αt2≥r时会选择保留产品,反之则继续选择退货。此时退货成功率为λ(t1+t2)。在部分退款退货期限t2内,退货失败的消费者只能保留产品。 在线零售商的利润为销售收入减去产品的订购成本(wQ)。 在线零售商的销售收入有六个来源: (1)全额退款退货期限t1内保留产品的消费者; (2)全额退款退货期限t1内成功退货的消费者; (3)未成功退货,在部分退款退货期限t2内选择保留产品的消费者; (4)未成功退货,在部分退款退货期限t2内选择继续退货并且退货成功的消费者; (5)未成功退货,在部分退款退货期限t2内选择继续退货但是再一次退货失败而只能保留产品的消费者; (6)所有未销售产品的残值。 所以,在线零售商利润的函数表达式如下: π=p[1-G(p-αt1)]Emin{Q,X}+ (p+s-p)H(t1)G(p-αt1)Emin{Q,X}+ p[1-H(t1)][G(p-αt1)-G(r-αt1-αt2)]Emin{Q,E}+ (p-r+s1)[1-H(t1)]H(t1+t2)G(r-αt1-αt2)Emin{Q,X}+ p[1-H(t1)][1-H(t1+t2)]G(r-αt1-αt2)Emin{Q,X}+ s[Q-Emin{Q,X}]-wQ 化简可得 π=Emin{Q,X}{p-(p-s)H(t1)G(p-αt1)+(s1-r)[1-H(t1)]H(t1+t2)G(r-αt1-αt2)-s}+(s-w)-wQ 令: Φ=p-s-(p-s)H(t1)G(p-αt1)+(s1-r)[1-H(t1)]H(t1+t2)G(r-αt1-αt2) 根据化简后的利润函数我们可以发现要求在线零售商利润的最大值,即求Φ的最大值。 定理1商品的最优价格 证明:通过对Φ求p的二次偏导得 观察p*的表达式我们可知,当消费者价值感知参数α变大时,意味着消费者在试用商品的时候可以获得更大的效用,这就代表消费者会更倾向于保留商品,而选择退货的消费者会变少。此时,商家可以选择提高售价来获得更高的利润。观察t1,我们可知,p关于t1是一个双曲线函数,且t1减少时p增大的速率远远大于t1增加时p增大的速率。也就是说,当没有法律法规强制要求的情况下,商家会尽可能提供较短的全款退货期限甚至不愿意提供全款退货的退货选项。观察参数λ,我们可以发现当λ较大时,即大多数消费者可以在规定的退货期限时间内完成退货,商家可以通过降低售价p来提高消费者保留商品的意愿,同时减少想要退货的人数G(p-αt),从而提高零售商的利润。 定理2零售商的最优退款 证明:通过对Φ求r的二次偏导得 观察r*的表达式可知,当α增大时,p也随着增大。由于α增大时,p也随之增大,如果零售商不提高退款r,会降低消费者购买的意愿。由于k>α,我们可以发现部分退款期限时间t2变大时,r随之变小。主要原因是退款期限时间t2越大,表示消费者可以试用产品的时间越长,由于人的逐利性,消费者会试用到退货期限时间再进行退货,所以商品价值由于人为的使用而不可避免地造成损失,所以零售商需要通过降低退款r来弥补损失。也可以理解为,商品使用的时间越长,退货后,商家对商品需要重新包装、修复的重新上架费越高。 命题1最优退货期限时间有以下性质: (1)当l≠s+kt1,且s-l>2kt2+3αt1即t21<0时; (2)当l≠s+kt1,且l+2kt1+3αt1≥s>l+αt1,即t21≤0,t22>0时; (3)当l≠s+kt1,且s≤l+αt1,即t22≤0 (4)当l=s+kt1时: 证明:将r*和p*和代入Φ: Φ=p-s-(p-s)H(t1)G(p-αt1)+ (s1-r)[1-H(t1)]H(t1+t2)G(r-αt1-αt2) Δ=B2-3AC= 当Δ=B2-3AC>0时,即l≠s+kt1时,Φ有极值。通过计算可得极值点为 Φ关于t2的图像如图1所示。 图1 Δ>0时,Φ关于t2的图像 当Δ=B2-3AC=0,即l≠s+kt1时,Φ关于t2单调递增 。Φ关于t2Φ的图像如图2所示。 图2 Δ>0时,Φ关于t2的图像 令t0=0,T=T23。 定理3零售商最优订货量为: 假设消费者对某商品的估值服从均匀分布v~U(60,120),市场需求服从均匀分布X~U(0,100),产品的批发价格w=80,未销售的产品残值s=75,产品生命周期T=30,全额退款退货期限t1=7,产品价值的衰减率k=1.5。 表2 p随α和λ的变化情况 表3 r随α和λ的变化情况 表4 Q随α和λ的变化情况 表5 π随α和λ的变化情况 通过观察以上四张表,不难发现p、r、Q、π都随着α的增大而增大,随着λ的变大而变小。也就是说,消费者在试用产品的时候所能获得的感知效用越高,消费者就更愿意将产品保留,选择退货的消费者就越少,零售商就可以选择提高售价和订购数量来获得更高的利润。同理,λ越大,意味着在全款退货期限内想要退货并且能够在期限内完成退货的消费者比例越高,这时候只有少数消费者未能及时完成退货,此时这部分消费者就需要通过比较v与r-αt1-αt2的大小重新考虑是否退货。所以,零售商可以通过降低售价来减少想要退货的消费者人数,从而提高销售利润。1.2 符号说明

1.3 消费者退货行为分析
1.4 在线零售商利润模型的构建
2 模型求解

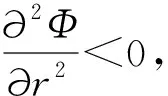

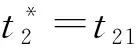

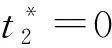
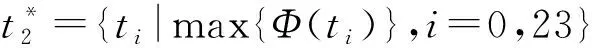
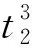
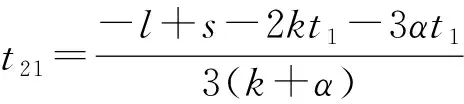
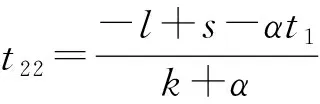


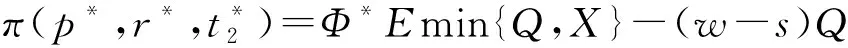
3 算例分析