基于核心化技术的点覆盖改进算法

骆伟忠，蔡昭权

(惠州学院信息科学技术学院,广东 惠州 516007)

1 引言

点覆盖是Karp的21个NP完全问题之一，除非P=NP，否则无法在多项式时间内求解问题的最优解[1]。点覆盖在社交和通信网络、生物信息学、超大规模集成电路等领域具有越来越重要的应用[2,3]。

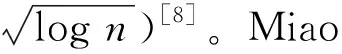
近来，人们从参数计算角度研究点覆盖的最优化求解。Buss等人[10]首次提出时间复杂度为O(kn+2kk2k+2)的参数精确算法，其中k为问题解的大小。随后，Balasubramanian等人[11]将底数降低到2以下，给出一个时间为O(kn+1.32kk2)的参数算法。目前，针对该问题的最好结果是Chen等人[12]基于分支限界技术提出的时间复杂度为O(1.27k+kn)的算法。文献[13]研究点覆盖在保证值以上的参数复杂性和参数算法设计。

针对点覆盖的参数算法研究和启发算法研究是两条独立线路，现有研究都没有综合两者进行算法设计或优化。本文提出结合核心化操作和启发式操作的算法框架，利用参数计算中的核心化技术进行点覆盖的启发式算法优化。启发或近似算法基于贪婪或随机策略，无法实现全局最优；而核心化操作对问题实例“难处理部分”无能为力。利用核心化技术，通过深入分析图中顶点间的组合特性，挖掘出图中必定属于全局最优点覆盖的顶点集。在原有启发算法贪婪选择顶点前执行核心化过程，将属于全局最优的点集放入解中，从而提高解的精度。另一方面，启发式操作进行了顶点或边的删除，改变了问题实例的原有结构，为下一轮的核心化操作提供可能。在随机拓扑网络和真实生物网络上的测试表明，新算法在各种不同网络实例中对原有算法进行了不同程度的优化。特别是在稀疏网络中，新算法在大部分网络实例中得到了最优解，且运行时间与原有算法相当。

2 预备知识

设G(V,E)为一个无向、简单的连通图，其中V是G的顶点集，E是G的边集。对于u,v∈V,如果u与v相邻，则用(u,v)表示u、v之间的边。设v∈V，e=(u,v)∈E，Gv表示从图G中删除v以及依附于v的边，Ge表示从图G中删除u、v以及依附于u、v的边。设U⊆V,则G[U]表示U在图G上的导出子图。设e=(u,v)∈E，则顶点v(或u)能覆盖边e。

定义1(点覆盖给定图G(V,E)) 设C⊆V,如果对于图G上的任何一条边e∈E，存在顶点v∈C，使得v能覆盖e,则称C为图G的点覆盖。

设C⊆V为图的某个点覆盖,如果图G的任何点覆盖C′⊆V，满足|C′|≥|C|，则称C为图G的最小点覆盖。

3 现有算法分析

点覆盖是NP难解问题，人们普遍认为需要指数时间求解该问题的最优解。但是，指数时间在实际中不可用，人们主要从启发式算法或近似算法的角度在多项式时间内求解该问题的非最优解。

针对点覆盖，最为著名的算法为Nixon提出的近似率为logn的算法和Fanica提出的近似率为2的算法[6,14]。Nixon提出的算法的基本思想是重复选取当前图G中度最大的顶点v放入解中，并从图G中删除v以及依附于v的边，如算法1所示(为便于描述，将Nixon提出的近似率为logn的算法命名为AppV，而Fanica提出的近似率为2的算法命名为AppE)。

另一近似算法的基本思想是不断选取当前图G中任意一条边e=(u,v)，将u和v放入解中，并从G中删除u、v以及依附于u、v的边。

通过分析以上两个算法可发现，启发式或近似算法的本质是通过牺牲解的精确性来换取时间效率。因此，其主要缺陷是其解题步骤是一种“启发式操作”，通常能实现局部最优，但无法实现全局最优。

核心化是多项式时间处理NP难解问题的一种新技术。该技术对问题实例中“易处理部分”进行处理，识别出属于全局最优解的元素。问题实例经过核心化处理后，得到“难处理部分”。除非打破“难处理部分”的结构，否则核心化过程无法继续进行。

算法1AppV算法

输入：G(V,E)。

输出：V的子集D。

1D=∅；

2 WhileE≠∅ do{

2.1 选取G中度最大的顶点v;

2.2D=D∪{v}；

2.3G=Gv;}

3 ReturnD;

启发式操作和核心化操作是多项式时间处理NP难解问题的有效方法。但是，启发式操作无法实现全局最优，而核心化操作对问题实例“难处理部分”无能为力。

4 改进算法

新算法融合启发式操作和核心化操作，两者重复轮流执行，如图1所示。首先进行核心化操作，对问题实例中“易处理部分”进行处理，将属于最小点覆盖的点集放入解中，并删除某些不属于最小点覆盖的顶点。经过核心化处理后，问题实例仅剩下“难处理部分”。接着执行启发式操作，贪婪选择实例中顶点放入解中。启发式操作打破了实例的原有结构，为下一轮的核心化操作提供可能。重复以上过程，直到问题实例中不存在边，完成问题求解。

Figure 1 Algorithm framework 图1 算法框架

核心化过程会将属于最优点覆盖的顶点集加入解中，实现全局最优，从而提高解的精确性。该算法框架可以对点覆盖现有的任何启发式或近似算法进行优化。这里以近似算法AppV为例说明具体的优化过程。

4.1 核心化操作

首先给出针对图中度为0、1或2的规约规则。

规则1设v∈V为图G上一个度为0的顶点,则从G中删除v。

度为0的孤立点，不能覆盖任何边，因此可以直接删除。

规则2设v∈V为图G上一个度为1的顶点，w∈V为v的邻接点,将w放入解D中，并从G中删除v和w。

v和w中至少有一个顶点在解中。同时，注意到顶点w的度至少为1，其覆盖的边数不会少于v覆盖的边数，因此优先将w放入解中。

规则3[12]设v∈V为图G上一个度为2的顶点，w1,w2∈V为v的两个邻接点，且w1和w2相邻，则将w1和w2放入解D中，并从G中删除v、w1和w2。

v、w1和w2中至少有两个顶点在解中，w1和w2组合的覆盖能力比其它大小为2的顶点组合覆盖能力强，因此优先将w1和w2放入解中。

规则4[12]设v∈V为图G上一个度为2的顶点，w1,w2∈V为v的两个邻接点，且w1和w2不相邻，则对w1或w2的所有邻接点w(w≠v)，将边(v,w)加入G中，并将w1和w2从G中删除。

对于G上的最优点覆盖D，D如果包含v，则不包含w1和w2；如果不包含v，则一定包含w1和w2。规则4不能确定是v，还是w1和w2在最优解中。因此，该规则执行后需保存v、w1和w2信息以构造问题输入实例上的解。

接下来给出基于线性规划的规约规则。

点覆盖可以表示为一个线性规划问题[15]。假设给定的图为G(V,E),对于图G的每一个顶点v∈V，构造变量xv，xv的取值为0≤xv≤1，点覆盖可以转变为以下线性规划问题：

最小化：∑v∈Vxv。

约束：对于每条边(u,v)∈E,满足xu+xv≥1;对于每个与顶点v对应的变量xv，满足0≤xv≤1。

求解以上线性规划，可将V中顶点划分为三部分：

C0={v∈V|xv>0.5};

V0={v∈V|xv=0.5};

I0={v∈V|xv<0.5}。

引理1[15]给定点覆盖实例G(V,E),设C0、V0、I0为按以上方式求解得出的顶点子集,则G上存在最小点覆盖S，使得C0⊆S,S∩I0=∅。

引理1表明，存在某个最小点覆盖包含C0中的所有点，同时不包含I0中的任何点。

基于引理1，得出核心化的下一条规则。

规则5设C0、V0、I0为按以上方式求解得出的顶点子集,将C0放入解D中；并将I0与C0从G中删除，即G=G[V0]。

规则5将线性规划得到的点集C0放入解中，并从G中删除C0∪I0以及依附于其上的边。问题规模降低为G[V0]。

接下来证明V0的规模与G[V0]最小点覆盖大小之间的关系。

□

由规则1～规则5得出针对点覆盖的核心化过程Kernel，如算法2所示。

算法2Kernel (G(V,E),D)算法

1 WhileE≠∅ Do{

1.1 WhileE≠∅ Do{

1.1.1 执行规则1；

1.1.2 执行规则2；

1.1.3 执行规则3；

1.1.4 执行规则4；

1.1.5 如果规则1～规则4均没有被成功执行，则退出当前循环；}

1.2 执行规则5}

2 Return

步骤1.1.1～步骤1.1.4均会在图G中寻找满足规则执行条件的局部结构，若存在则执行规则并进入下一步骤。某规则没有被成功执行，表示当前图中不存在满足该规则执行条件的局部结构。规则5因为要执行线性规划，是所有规则中最费时的，所以放到最后执行。只有当执行时间较快的规则1～规则4均不能被成功执行时，才会执行规则5。

4.2 基于核心化的算法

基于核心化操作，提出改进的算法Kernel_AppV，如算法3所示。Kernel_AppV在贪婪选择顶点前进行核心化操作。

算法3Kernel_AppV算法

输入：G(V,E)。

输出：V的子集D。

1D=∅；

2 WhileE≠∅ do{

2.1Kernel(G,D);

2.2 选取G中度最大的顶点v;

2.3D=D∪{v}；

2.4G=Gv;}

3 根据D构造输入实例上的解D′;

4 ReturnD′

核心化操作将属于全局最优解的点集放入解中，提高了解的精度。同时，核心化操作会将实例中不属于最优解的点集删除，降低实例规模，并保证核心化后结果图中超过一半的顶点属于最优解，这提高了后续贪婪选择的顶点属于最优解的概率。另一方面，核心化后续的贪婪操作会改变图的结构，使得图结构满足核心化的执行条件，从而使下一轮的核心化操作能继续进行。核心化操作和贪婪操作是一对相互促进的操作。

步骤3根据D以及规则4执行时保存的顶点信息，来构造问题输入实例上的解：如果D包含规则4中保存的顶点v，则用w1和w2替换v；如果不包含v，则加入v。

核心化操作并不会降低原有算法的近似率，接下来给出理论上的证明。

定理2算法Kernel_AppV的近似率为2。

□

定理2表明，在原有近似算法中加入核心化操作，不会使算法的近似率变差。原算法AppV的近似率为logn，加入核心化操作后改进到2。

5 仿真实验

为了测试新算法Kernel_AppV的有效性，通过仿真实验将其与点覆盖经典近似算法AppV进行比较。算法Kernel_AppV和AppV均为多项式时间的近似算法，无法对任何实例得到最优解。为了更好地进行测试，使用分支技术求解出问题实例的最优解作为比较标杆。使用的分支技术能得到问题任何实例的最优解，但需花费指数时间。实验平台配置为：Intel i3-3110M,主频 2.40 GHz,4 GB内存。

实验在随机网络和实际生物网络中进行。生物网络来源于DIP数据库的蛋白质相互作用网络[16]。随机网络的生成方法如下：给定代表网络节点个数的n和网络边条数的m，首先产生一个节点个数为n的且不包含任何边的网络G；然后逐渐往网络G中添加m条边，对n个顶点从0到n-1进行编号。随机产生两个在0和n-1之间的代表顶点的不同数字v和w，如果边(v,w)不在G中，则将其添加到G中；重复以上过程，直到G中边的条数为m。通过设置n和m的大小来控制网络的规模和稀疏度。

5.1 随机网络

核心化操作和启发式操作是一对互补的操作，核心化操作提高了解的精度，而启发式操作改变了网络拓扑的原有结构，为下一轮的核心化操作提供可能。主要从以下三方面进行测试：核心化操作的优化效果、启发式操作对核心化过程的促进和算法时间效率。

(1) 核心化操作对解精度的提高。

测试在不同规模和不同稀疏度的网络上进行。表1～表3展示的是网络规模n为30，网络中边数m分别为50、100、300的结果。每组测试中生成500个随机实例。求解最优解的时间复杂度随网络规模n指数增长。因此，考虑到时间效率，将n设置为30。表中行表示算法的名称，列表示差值，即算法求解得到的解的大小与最优解大小的差值。

表1中边m为50，代表的是稀疏网络。算法Kernel_AppV在500个实例中得到的解均为最优解；算法AppV在240个实例中取得了最优解，大部分实例中求得的解比最优解大1或2，最差情况下比最优解大3。

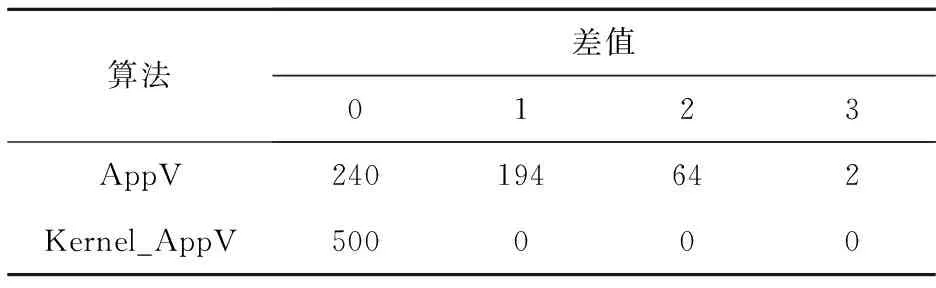
Table 1 Optimization in sparse networks (n=30,m=50)

表2中边m为100，代表的是中等稠密网络，算法Kernel_AppV性能有所下降，在451个实例中取得了最优解。

Table 2 Optimization in moderatelydense networks (n=30,m=100)

表3中边m为300，代表的是稠密网络，算法Kernel_AppV和算法AppV的差距在缩小，算法Kernel_AppV取得最优解的实例降低到391；而算法AppV取得最优解的实例上升到309。

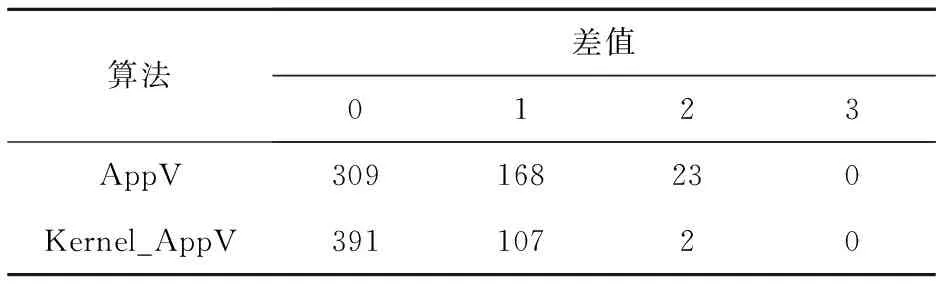
Table 3 Optimization in dense networks (n=30,m=300)

表1～表3的结果表明，算法Kernel_AppV的性能与网络稀疏度相关。图2的结果进一步展示了稀疏度对算法优化的影响。将网络规模n设为30个顶点，边数m从30逐步增加到330(步长为20)。当边数逐步增加时，网络的密度也逐步增加。对于特定的n和m，生成100个不同的测试实例。图2中的横坐标表示边数，纵坐标表示在100个实例中，算法Kernel_AppV取得的解比算法AppV取得的解要严格小的实例个数。从图2的整体趋势来看，算法Kernel_AppV在稀疏网络上对算法AppV的优化效果较好。随着网络稀疏度的增加，算法Kernel_AppV对算法AppV的优化次数下降。其主要原因是核心化操作中的规约规则主要针对的是网络中的低度顶点。当网络较稀疏时，低度点较多，解中的顶点大多数来自核心化操作。

Figure 2 Impact of network density on optimization performance 图2 网络稠密度对优化性能的影响

图3为网络规模增加后，Kernel_AppV和AppV两个算法的性能对比。网络规模n设为500个顶点，边数m设为1 000。随机生成50个实例进行测试。从图3可看出，在50个实例中，算法Kernel_AppV得到的解大小均比算法AppV得到的解要小，表明Kernel_AppV在网络规模较大时，仍能取得较好的优化效果。

Figure 3 Optimization in relatively large scale networks图3 较大规模网络上的优化

(2)启发式操作对核心化过程的促进。

启发式操作会改变网络拓扑的结构，为下一轮的核心化操作提供可能。表4展示启发式操作的执行情况。当n=100，m=100时，该网络实例是稀疏结构，核心化操作单独完成整个解的求解。但是，当网络的边增加到200时，网络稠密度增加，核心化操作不能完成整个解的求解。有三次核心化操作无法继续执行，这时启发式操作将相关顶点放入解中并将该顶点删除，改变了网络的结构，从而使得核心化操作能够继续执行。当m=300和m=500时，网络稠密度进一步增加，启发式操作参与的次数也随之增加。

Table 4 Execution of heuristic operation

(3) 时间代价。

算法Kernel_AppV相比算法AppV取得了较好的优化效果，但其付出的主要代价是算法运行时间增加了。在500个顶点、500条边的随机网络上，算法Kernel_AppV和算法AppV的运行时间分别为125 ms和78 ms。两者运行时间相当，这是因为，此时该网络是稀疏结构，核心化操作中的规则1～规则4几乎完成整个解的求解，而耗时的规则5的执行次数很少。注意到规则1～规则4的执行时间与启发式操作执行时间相当。保持网络规模500不变，而边增加到1 000，算法AppV的运行时间增加到94 ms，而算法Kernel_AppV的运行时间急剧增加到15 978 ms。这是因为，当边增加时，网络稠密度增加，耗时的线性规划的执行次数也相应增加。

从以上分析可以发现，算法Kernel_AppV通过增加算法运行时间获得了解的优化。点覆盖是一个NP难解问题。最优化求解该问题，人们普遍认为不能在多项式时间内完成。现有实现点覆盖最优化求解的算法均付出了指数时间代价，一般情况下，指数时间是实际不可解的。算法Kernel_AppV在几乎所有稀疏网络实例上都获得了最优解，其代价是在原有多项式时间的启发式算法AppV上增加了多项式时间。使用传统方法需要付出指数时间的代价，而算法Kernel_AppV仅付出多项式时间代价。因此，算法Kernel_AppV以较低的时间代价获得了较好的解优化效果。

5.2 生物网络

使用DIP数据库20101010的酵母相互作用网络数据。去除网络中的自相互作用和重复相互作用后，网络中包含5 093个蛋白质和24 743对相互作用。该网络可抽象为一个无向图：每个蛋白质抽象为一个顶点，如果两个蛋白质间存在相互作用，则对应的两个顶点间添加边。

算法Kernel_AppV求解得到的解大小为2 109个顶点，而算法AppV求解得到的解大小为2 153个顶点。算法Kernel_AppV中由核心化操作得到的顶点个数为2 094，启发式操作得到的顶点个数为15。注意到核心化操作求解得到的顶点均属于某最优解，因此该解非常接近最优解。核心化操作能够完成几乎整个解的求解，主要原因是该生物网络是稀疏结构，且网络中存在大量的度为1和2的顶点，核心化操作能处理实例中绝大部分的顶点和边。

算法Kernel_AppV的运行时间为8.7 s，而算法AppV的运行时间为51.8 s。算法Kernel_AppV的执行速度比算法AppV的执行速度更快，表明在某些大规模稀疏网络中，算法Kernel_AppV的时间效率更高。

5.3 对其它算法的优化

采用与算法Kernel_AppV对算法AppV优化的类似过程，核心化操作可以对任何其它点覆盖近似算法或启发式算法进行优化。

图4展示的是对Fanica提出的近似率为2的近似算法的优化。其中AppE为原算法，Kernel_AppE为引入核心化过程后的新算法。从图4可发现，Kernel_AppE对AppE平均优化的个数为10左右。

Figure 4 Optimization for algorithm AppE图4 对算法AppE的优化

6 结束语

针对启发式或近似算法无法实现全局最优的不足，提出融合启发式操作和核心化操作的点覆盖通用算法优化框架。核心化操作和启发式操作循环交叉执行，核心化操作挖掘全局最优的顶点集，启发式操作改变网络拓扑结构，使得下一轮核心化能够继续，两者共同作用实现点覆盖求解的优化。实验表明，本文提出的新算法在随机网络和生物网络等各种不同的网络实例中均能实现优化。特别是在稀疏网络中，该算法运行时间与原有算法相当，在大部分实例中能得到最优解。下一步研究可考虑提出针对高度顶点的规约规则，对稠密网络进一步优化。另一方面，可将提出的算法优化框架应用于其它难解问题求解的优化。