基于极限学习机与改进K-means算法的入侵检测方法

王琳琳，刘敬浩，付晓梅

(1.天津大学电气自动化与信息工程学院，天津 300072；2.天津大学海洋科学与技术学院，天津 300072)

1 引言

随着互联网的飞速发展，网络的设计缺陷与安全漏洞带来了一系列的安全问题，必须采用主动防范的入侵检测技术来改善网络的安全状况。1998年哥伦比亚大学的Lee等人[1]将数据挖掘技术引入到入侵检测系统中，他们证明了可以使用数据挖掘技术发现用户和程序的特征模式，通过相关特征训练分类器可以达到识别入侵的目的。

近年来，学者针对如何将数据挖掘技术应用到入侵检测之中做了大量的研究。文献[2-4]分别讨论了支持向量机SVM(Support Vector Machine)、BP神经网络以及朴素贝叶斯算法等数据挖掘算法在入侵检测中的应用。但是，这些传统的算法存在一些问题，例如需要人工调整的参数较多、检测精度不高、容易陷入局部极小值、需要耗费大量的计算时间等。2006年Huang等人[5]提出了极限学习机ELM(Extreme Learning Machine)，ELM是一种针对单隐含层前向神经网络的新算法。ELM算法的输入层与隐含层间的连接权重向量以及隐含层神经元的阈值是随机产生的，此二者在训练过程中无需调整。ELM算法只需要设定隐含层的神经元个数，同时ELM算法不需要迭代，训练速度非常快。与传统算法相比，ELM算法具有学习速度快、泛化性能好等优点，因此适用于对入侵攻击的分类检测。但是，ELM算法对于激活函数的选择具有依赖性，激活函数选择的好坏直接影响着分类效果。文献[6]提出了一种基于核函数的ELM入侵检测分类方法，该方法采用径向基RBF核函数(Radial Basis Function)来代替ELM隐含层的激励函数。但是，由于部分攻击连接与正常网络连接的差异较小，进而影响了ELM算法在入侵检测中的效果。聚类分析作为一种常用的数据挖掘技术，其算法简单、计算复杂度低，适用于入侵检测系统。Portnoy等人[7]较早提出了基于聚类分析的入侵检测技术，利用无标签的数据进行训练，从而检测出未知攻击。K-means算法是经典的聚类算法。文献[8]将K-means算法应用于入侵检测之中。但是，传统的K-means算法的聚类结果受初始簇中心点的影响严重，初始簇中心点选取不当很容易造成聚类结果陷入局部最优解或导致错误的聚类结果，很多学者针对这个问题进行了研究。文献[9]提出了一种改进的半监督K-means算法，利用有标签的数据获得初始聚类中心。文献[10]采用加权局部方差结合最大最小法，优化K-means初始聚类中心的选取。但是，经过这些改进后的K-means算法仍然局限于人工设置初始聚类簇数目，而不是根据特征本身来确定聚类簇数目，使得聚类结果不稳定。多级分类的入侵检测方法可以提高入侵检测系统的准确率。文献[11]提出了基于多级神经网络分类的入侵检测方法，根据攻击类别分别训练神经网络，进而对不同种类的攻击进行分类。在多级模型的基础上结合多种数据挖掘方法，可以集成多种算法的优点。文献[12]提出了结合了贝叶斯聚类和决策树算法的多级混合入侵检测分类器。文献[13]提出了结合改进的CatSub算法、K-point算法等算法的多级混合入侵检测方法。

为了解决传统单一算法难以对不同攻击进行有效检测的问题，基于算法级联的思想，本文提出了一种结合ELM和改进的K-means算法的混合式入侵检测方法。仿真结果表明，本文所提出的入侵检测方法可以提高对入侵攻击的检测效率，并可以降低误报率。

2 基于PReLU激活函数的极限学习机算法

2.1 极限学习机理论

典型的单隐含层前向神经网络SLFNs(Single-hidden Layer Feedforward Neural networks)结构如图1所示，由输入层、隐含层与输出层三层组成。

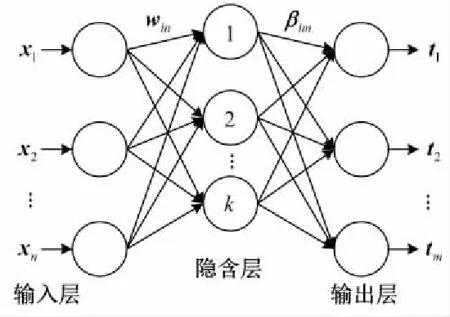
Figure 1 Structure of single-hidden layer feedforward neural networks图1 单隐含层前向神经网络结构

给定N个任意不同的样本xi,ti，xi=[xi1,xi2,…,xin]T∈Rn，ti=[ti1,ti2,…,tim]T∈Rm，其具有k个隐含层神经元的SLFNs输出函数可表示为：

j=1,2,…,N

(1)

其中,g(x)为激活函数，wi=[wi1,wi2,…,win]T为输入层与第i个隐含层神经元间的连接权重向量，βi=[βi1,βi2,…,βim]T为第i个隐含层神经元与输出层间的连接权重向量，bi为第i个隐含层神经元的阈值，oj为第j个输入样本对应的输出值。

给定k个隐含层神经元和激活函数g(x)，则存在wi,βi,bi使得SLFNs能以零误差逼近这N个任意不同的样本xi,ti，即:

(2)

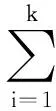
(3)

式(3)可表示为:

Hβ=T

(4)

其中,

Hw1,…,wk,b1,…,bk,x1,…,xN=

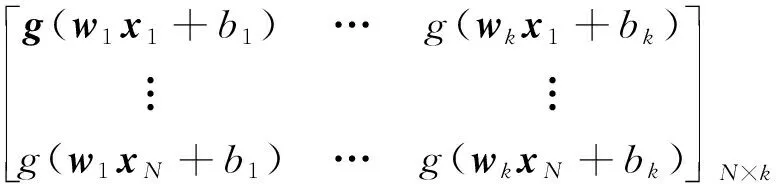
(5)

其中，H是该神经网络的隐含层输出矩阵，H的第i列是第i个关于输入x1,x2,…,xN的隐含层节点输出。

极限学习机ELM算法是一种求解SLFNs的学习算法。由Huang等人[5]的证明可知，当激活函数g(x)无限可微时，SLFNs的参数并不需要全部进行调整，w=[w1,w2,…,wk]n×k和b=[b1,b2,…,bk]T可以随机选择，且在训练的过程中保持不变，而β可以通过求解以下方程组的最小二乘解获得:

β-T‖

(6)

其解为:

(7)

其中，H+为隐含层输出矩阵H的Moore-Penrose广义逆。

2.2 基于PReLU激活函数的极限学习机算法

激活函数选择得是否合适直接影响极限学习机ELM的学习效果。传统的ELM算法采用的激活函数是S型非线性连续光滑单调的Sigmoid函数，其函数定义为:

(8)

由Huang等人的证明可知，ELM可选择一个任意区间无限可微的函数作为激活函数，所以激活函数的选择并不唯一。文献[14]提出了一种修正线性单元ReLU(Rectified Linear Units)的新型激活函数，ReLU激活函数具有稀疏激活性，在深度卷积神经网络中的训练时间优于传统的Sigmoid函数[15]。ReLU激活函数的定义为:

g(x)=max(0,x)

(9)

文献[16]在ReLU激活函数基础上提出了参数修正的线性修正单元PReLU(Parametric Rectified Linear Unit)。PReLU作为ReLU函数的改进函数，引入了修正参数，提高了神经网络的准确率，而所增加的计算量可以忽略不计。PReLU引入了非常少量的额外参数，额外参数的数量等于信道总数，考虑权重总数时这是可以忽略的，所以PReLU函数不会造成过度拟合以及导致额外的风险。所以，本文将PReLU函数作为激活函数以优化ELM的学习效果。PReLU函数定义为：

g(x)=max(0,x)+amin(0,x)

(10)

3 改进的K-means算法

3.1 K-means算法

1967年MacQueen[17]提出了K-means算法，该算法是一种基于划分的经典的聚类算法，其聚类结果使相似度较高的样本聚集到同一类簇，而不同类簇间的样本相似度较低[18]。K-means算法的基本思想是：首先随机选取k个点作为初始聚类中心，然后计算各个样本到聚类中心的距离，把样本归到离它距离最小的聚类中心所在的簇，对调整后的新簇重新计算平均值得到新的聚类中心，以上过程不断重复，直至相邻两次的聚类中心没有任何变化，即准则函数收敛。

K-means算法在计算两个样本之间的距离时，考虑到入侵检测系统对于算法复杂度的要求，一般采用算法复杂度较小的欧氏距离，计算公式如下：

d(xi,xj)=

(11)

其中,xi=[xi1,xi2,…,xip]与xj=[xj1,xj2,…,xjp]是两个维度为p的数据对象。

K-means算法常采用误差平方和作为准则函数，其定义如下：

(12)

其中,x是所在聚类空间的数据对象，k为聚类簇的总数，mi为聚类簇Ci的中心，即平均值。

3.2 改进的K-means算法

传统的K-means算法随机选择初始聚类中心，而不同的初始中心会导致不同的聚类效果，如果初始聚类中心选择不当，很容易陷入局部最优。同时，传统的K-means算法需要人为事先确定聚类数目k，但是算法不能分辨出所设定的聚类数目是否合适。因此，本文提出一种通过设定距离阈值来选择初始聚类中心，同时可以通过计算自动生成聚类数目k，最终通过比较数据点与邻近点的距离从而进行聚类改进的K-means算法。

对训练集中的正常网络连接以及与正常网络连接特征相似的攻击，分别采用改进的K-means算法进行聚类，生成若干种类的聚类中心数据集，以聚类得到的聚类中心数据集作为新的高质量的训练数据集。

改进的K-means算法描述如下：

算法1改进的K-means算法

输入：数据集D,距离阈值λ。

输出：聚成k类的聚类中心数据集D′。

步骤1随机选择αj∈D作为第一个聚类中心c1，令k=1；

步骤2For(∀αi∈D,i≠j)

步骤3If(欧氏距离d(αi,cn)>λ,n=1,…,k)

步骤4k=k+1//αi为新的聚类中心ck

步骤5End If;

步骤6以cn为中心，计算欧氏距离d(αi,cn)，将ai划分到dmin(αi,cn)的类cn中；

步骤8End For;

步骤9For(∀αi∈D)

步骤10重复步骤6,步骤7；

步骤11If (生成的聚类中心cn保持稳定)

步骤12输出聚成k类的聚类中心数据集D′；

步骤13End If;

步骤14End For;

将改进的K-means算法与投票策略结合进行入侵检测。对于测试集中的每一个样本点β，分别计算其与改进的K-means算法中得到的每一个聚类中心cn的欧氏距离。选取其中距离最小的m个点，并判断这m个聚类中心所属的攻击类别，取数量最多的聚类中心的类别作为β的类别，若聚类中心类别的数目出现相等的情况，则将β归于与其距离最近的点的类中。

4 入侵检测数据集与检测算法流程

4.1 NSL-KDD数据集

NSL-KDD数据集[19]一种比KDD CUP99[20]数据集更新的用于入侵检测测试的数据集。作为KDD CUP99数据集的改进版，NSL-KDD数据集解决了KDD CUP99数据集中数据冗余的问题，避免了分类器在训练与分类过程中偏向于频繁出现的连接数据。NSL-KDD数据集中仅包含网络流量数据，每一条数据网络连接数据由41个网络连接属性值以及一个类别标签构成。NSL-KDD的训练集中有125 973条网络连接记录，测试集有22 544条网络连接记录，包含了正常数据连接Normal以及39种攻击类型，这39种攻击类型分属于DOS、Probe、U2R以及R2L等四大类攻击，其中训练集中包含22种攻击，而测试集中多出了17种攻击，这些仅在测试集中出现的攻击类型，可以评价入侵检测算法对新型未知攻击的检测能力。

4.2 入侵检测算法流程

综合多种数据挖掘算法构建出的多级混合式入侵检测方法，可以集成多种算法的优点。很多学者提出了结合不同分类器的级联式入侵检测系统。文献[12]与文献[13]所提出的入侵检测模型在第一级对DOS与Probe攻击进行分类，第二级对Normal进行分类，第三级对U2R与R2L进行分类。文献[21]所提出的入侵检测模型在第一级对DOS与Probe攻击进行分类，第二级对U2R攻击进行分类，第三级对R2L与Normal进行分类。

本文所采用的检测模型如图2所示。由于DOS和Probe这两大类攻击在短时间内会向同一目的计算机发起大量的连接请求，其网络连接数据与Normal的网络连接数据差别很大，所以在第一层与第二层分别采用基于PReLU激活函数的ELM算法对这两大类攻击进行检测。而在U2L与R2L这两大类攻击中黑客需要获得受害者计算机的非法访问权限，所以生成的网络连接记录将与正常用户的网络连接记录非常相似，同时这两类攻击的数量相对较少，因此在第三层采用改进的K-means算法结合投票策略对Normal、U2R与R2L进行分类。

Figure 2 Architecture of the intrusion detection model图2 入侵检测模型结构

5 实验与结果分析

实验的硬件环境为2.20 GHz Intel Core i5 CPU，4 GB RAM计算机，软件环境为Matlab R2014a。本文采用NSL-KDD数据集进行仿真验证实验。

为了评价本文算法的检测效果，采用精确度、召回率、准确率、F1值、检测率与误报率等六项指标进行衡量。首先定义如下参数：

(1)TP(True Positive)：入侵攻击被判断为入侵攻击的网络连接数。

(2)TN(True Negative)：正常连接被判断为正常连接的网络连接数。

(3)FP(False Positive)：非入侵攻击被判断为入侵攻击的网络连接数。

(4)FN(False Negative)：入侵攻击被判断为正常连接的网络连接数。

基于以上参数，衡量指标的定义如下：

(1)精确度Precision=TP/(TP+FP);

(2)召回率Recall=TP/(TP+FN);

(3)准确率Accuracy=(TP+TN)/(TP+TN+FP+FN);

(4)F1值F1-measure=2*Precision*Recall/(Precision+Recall);

(5)检测率Detection Rate：总体测试集中被正确分类的数据所占的比例。

(6)误报率FalseAlarmRate=FP/(TP+FP)。

从NSL-KDD数据集的训练集与测试集中，各抽取10 000条数据进行算法有效性验证。实验数据的构成如表1所示。

Table 1 Composition of training and testing data sets

在进行模型训练之前，首先要对数据集中的数据进行预处理。对于数据的预处理可分为两个步骤：

(1)字符型特征转化为数值特征。

NSL-KDD数据集共有三种字符型特征，分别是协议类型(Protocol Type)、网络服务(Service)以及连接的状态(Flag)。将Protocol Type特征中的TCP标注为1，UDP标注为2，TCMP标注为3。将67种Service特征按名称首字母顺序分别标注为1～67，将11种Flag特征按顺序分别标注为1～11。将训练数据按照标注的攻击类型分为Normal、DOS、Probe、U2R以及R2L五类。

(2)标准化与归一化处理。

将由(1)得到的数据进行标准化与归一化处理，消除由于不同特征值度量单位的差异对实验结果产生的影响。标准化公式为：

(13)

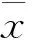
归一化公式为：

(14)

其中,x1min为标准化后该特征值的最小值，x1max为标准化后该特征值的最大值，x2为归一化后的结果。

对本文所提出的入侵检测模型进行参数设置。第一层与第二层ELM模型采用PReLU激活函数，参数a设置为0.25，隐含层神经元个数设定为200。第三层模型取每一条测试数据与经过改进的K-means算法生成的新训练集中距离最近的3个点，进行投票策略，其中改进的K-means算法的阈值设定分别是Normal为0.6，U2R为0.4，R2L为0.4。每次实验重复20次求平均值。将本文所提算法与BP、SVM和ELM算法进行比较。BP的隐含层神经元个数设定为30，lr为0.1，epochs为100，goal为0.001。SVM采用广泛使用的LIBSVM[22]软件包，SVM采用C-SVC类型，RBF核函数，gamma参数为0.11，惩罚因子C为256。ELM算法的激活函数为Sigmoid函数，隐含层神经元个数设定为200。每次实验重复20次求平均值，实验结果如表2和表3所示。

Table 2 Detection rate comparisonamong different algorithms

由表2的结果看来，本文所提出的检测方法对于Normal、Probe和DOS的检测率都有很好的效果。相比之下，U2R与R2L的检测率相对较低，这是因为U2R与R2L攻击在训练集的样本数量小于DOS与Probe攻击的，同时测试集R2L攻击中新出现了snmp get attack攻击与snmp guess攻击，这两种攻击的特征属性与Normal的特征属性高度相似，导致大多数R2L被误判为Normal。

Table 3 Detection result comparisonamong different algorithms

对比传统的BP、SVM和ELM三种算法，本文所提出的检测方法对于不同种类攻击的检测率都有提升，尤其是对U2R、R2L这两类攻击的检测效果有大幅度提升。由表3可知，本文所提出的算法具有较高的精确度、召回率以及F1值，在提高检测准确率的同时降低了检测的误报率，可以说明本文所提出的检测方法的有效性。

将本文所提出的检测方法与同样基于NSL-KDD数据集的其他检测算法进行对比，其他检测算法分别是文献[13]提出的多层混合式MLH(Mutil Level Hybrid)入侵检测方法、文献[23]提出的基于最大最小法K-means的入侵检测方法、文献[24]提出的基于人工神经网络ANN(Artificial Neural Network)的入侵检测方法，以及文献[25]提出的基于神经网络和K-means的混合算法进行入侵检测的FP-ANK方法，对比结果如表4所示。

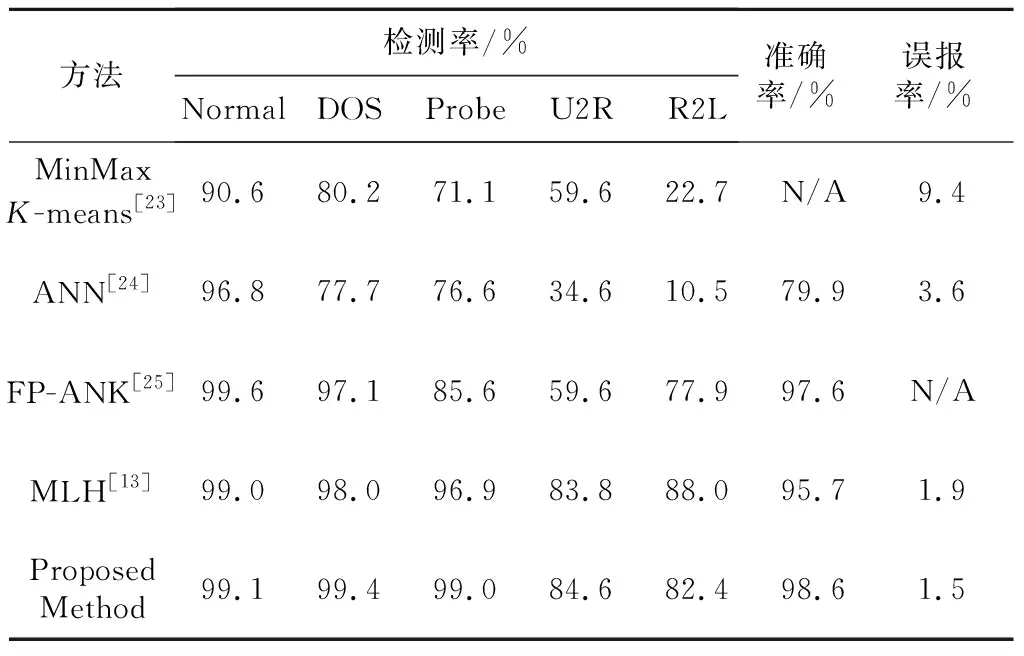
Table 4 Detection rate comparison of different methods

由对比结果可知，本文提出的检测方法与其他方法相比准确率最高，且误报率相比其他方法最低。基于最大最小法K-means的入侵检测方法对于各种攻击的检测效果较差，且误报率较高。ANN检测方法对于正常流量的检测效果较好，但是对于网络攻击的检测效果较差。FP-ANK检测方法对于Normal、DOS与Probe的检测率与本文所提出的检测方法基本相同，但是对U2R与R2L的检测率明显低于本文所提出的混合式检测方法。MLH检测方法对于五类网络流量的检测效果与本文所提方法基本相同，但是准确率和误报率低于本文所提出的方法。

6 结束语

本文采用基于ELM与改进K-means的混合式入侵检测方法，结合了不同算法的优点，提高了对于网络正常数据与异常数据的检测率，同时降低了误报率。基于PReLU激活函数的ELM算法提高了算法的分类效果，改进的K-means算法避免了初始中心选择不当对聚类效果的影响，同时改进的K-means算法与基于距离的投票策略提高了对攻击的分类效果。在今后的研究中，要进一步探索如何改进方法使其应用于实时网络当中。