基于贝叶斯方法的墙体传热系数实测反演分析

张 ，， ，

(1.哈尔滨工业大学 建筑学院 黑龙江省寒地建筑科学重点实验室，黑龙江 哈尔滨 150001；2.哈尔滨工业大学 建筑设计研究院，黑龙江 哈尔滨 150001)

我国是一个建筑大国，建筑面积已超过500亿m2，每年还有16～20亿m2的增量。建筑耗能占人类能源消耗的比例大约在30%～40%[1]。因此，建筑领域节能研究意义十分重大。我国严寒及寒冷地区面积占总面积的1/4以上，要减少暖通行业的能源消耗，除提升供热系统性能外，提升墙体的保温性能也是重要手段之一[2]，墙体保温性能的优劣将直接影响建筑节能表现。由于种种原因，如：保温设计缺陷、施工质量问题以及建筑材料质量问题等，外围护结构热工性能检测十分必要，亟待开发简洁、准确的围护结构热工性能检测方法。

墙体传热系数是重要的围护结构热工性能参数，极大地影响着严寒和寒冷地区的建筑能耗水平和室内舒适性，是建筑热工设计中需加以控制的最主要参数之一。建筑设计阶段通过保温设计计算确定墙体传热系数，并应符合相关标准[3]的要求。使用阶段的节能检测、绿色建筑评价等则不仅需要了解其设计值，更需要获得其实际值。特别是对于大量既有建筑，一般需要依靠现场实测手段获取墙体传热系数[4]，方法主要有：热流计法、热箱法、非稳态法和红外热像仪法等[5-6]。

热流计法假设围护结构处于一维稳态传热过程，建筑材料是一种各向同性、连续的介质。用热流计测得通过围护结构的热流密度，用温度传感器测得围护结构两侧表面的温度，根据算数平均法算出围护结构主体部位的热阻，进而根据规范中给定的围护结构内、外表面对流换热系数确定该围护结构的传热系数。该方法的局限性在于方法受室内、外温差影响较大，只有在较大温差条件下才可能得到理想结果[7]。热箱法是通过人力创造一个热环境，以满足节能检测标准，提高被测围护结构两侧的温度差，增大热流量，提高测试准确度。但该方法并不能进行现场测试。非稳态法[8]是在围护结构的内侧加一个平面热源，通过热源对围护结构进行加热，一段时间达到平衡后，测得围护结构内外表面的温度即可辨别出被测围护结构的传热系数。此方法目前仅可在实验室测试围护结构传热系数，不利于推广大范围应用。红外热像法是一种非接触式温度测量方法，具有测温速度快、测温范围广的特点，是一种快速测试技术。但由于受到气象条件、建筑室内使用情况等影响，目前仅能定性的分析被测物体表面的热工性能。

在墙体传热系数预估计值可能不够精确，并且测试环境等条件难以满足或者掌握不够全面的情况下，如能综合预估计信息和现场实测信息反演估计墙体传热系数数值会更有实际意义。本文采用一种计算假设概率的方法——贝叶斯方法，将既有建筑的调研结果作为先验概率分布的估计依据，通过现场实测信息搜集形成观测数据样本，从而实现先验信息与样本信息的综合[9]，结合贝叶斯公式得出后验信息，从而利用后验信息以概率分布函数形式表达建筑墙体传热系数。

1 理论模型建立

1.1 模型表达

贝叶斯统计方法中，一般利用先验概率分布表达模型参数预估计情况，在此基础上结合观测样本数据得到模型参数的后验概率分布，从而实现模型参数原有经验信息和样本数据信息的综合利用，以提高估计结果的准确程度。针对本文所研究的墙体传热系数的反演问题，可以采用以下的模型表示。

墙体传热系数反演估计中需要在现场实测之前确定先验分布，以作为墙体传热系数的预估计结果。工程中一般采用正态分布函数表达该分布，统计变量均值和方差可由墙体构造设计资料、建筑建造或改造年代等估计获得。墙体传热系数k的先验分布可以表示为k～N(μ,τ2)，即

在获得先验分布的基础上，反演估计还需要依靠现场实测完成。具体需要通过墙体内、外表面温度和热流密度的测试获取数据，计算得到传热系数的间接观测值，从而构成实测数据样本x，基于间接观测样本x=[x1,x2,…,xn]的似然函数为

现场实测过程中认为每次观测彼此不产生影响，作为间接观测值的墙体传热系数计算值服从正态分布N(k,σ2)，且相互独立。其中，传热系数k值为待反演估计参数，方差σ2值可以由数据样本统计分析或者测试仪表精度、量程确定。

依据贝叶斯统计理论，结合样本观测值x以及墙体传热系数k先验分布的联合概率密度函数可以表达并简化为

应用墙体传热系数检测设备获取观测数据样本x，其边缘分布可以表示为

(4)

其中，l2为与观测数据无关的系数。在上述条件下，贝叶斯统计理论分析结果表明墙体传热系数的后验概率分布也服从正态分布，数值上等于联合概率密度与边缘概率之比，可以表示为[9]

此外，如果现场实测难度较大，或者观测数据数量不足的情况下，可以依据测量误差传递理论估计其中统计变量。例如，采用热流计法进行墙体传热系数的检测中，墙体传热系数的表达式可以简化为k=k(ti,te,q)=q·(ti-te)-1。测量误差传递理论认为间接观测量的观测误差由各直接观测量的误差以及观测量间的函数关系式共同确定。对于本文所讨论的问题，墙体传热系数的方差可以表示为

1.2 方法步骤

总结上述内容，基于贝叶斯方法的墙体传热系数反演估计可以概括为以下步骤。

(1)调研待测试既有建筑，获取墙体构造或建筑建造、改造年代等信息；

(2)根据调研信息形成对墙体传热系数的预估计，并通过统计分析确定先验分布；

(3)采用如热流计法等现场检测方法获得若干温度和热流密度观测数据，并通过计算得到墙体传热系数样本数据；

(4)采用统计方法处理样本数据，回归生成观测数据样本的均值和方差；

(5)由测试仪表精度等级和量程等信息估计间接观测量的均值和方差；(现场实测数据充足时略过此步；数据不足或不能满足分析要求时利用该步骤替换步骤(3)和(4))；

(6)依据贝叶斯统计方法确定墙体传热系数的后验分布，表达墙体传热系数反演估计结果。

该方法基本流程如图1所示。

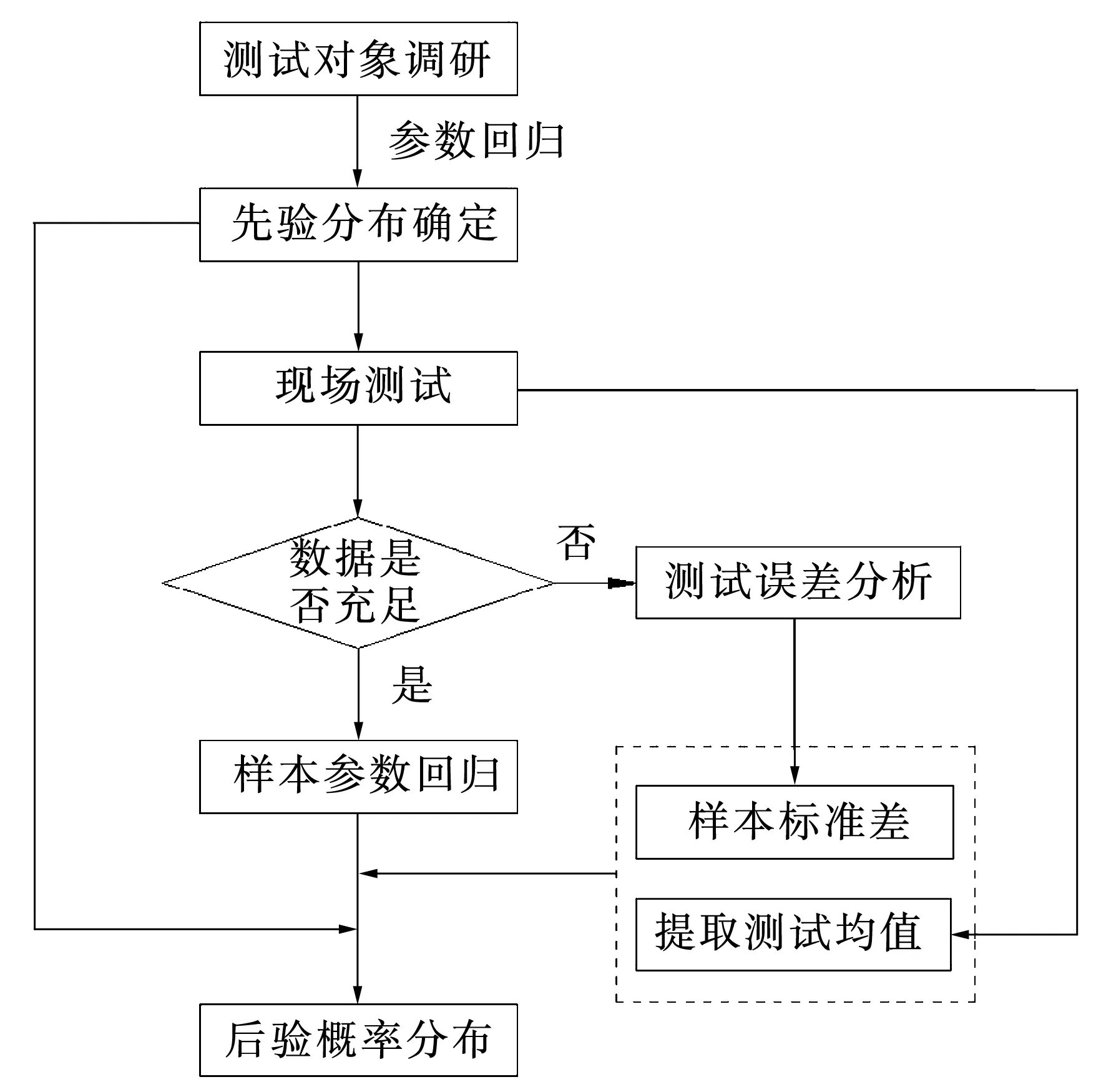
图1 墙体传热系数反演估计基本流程

2 测试实例分析

2.1 测试项目概况

本文将通过一个实测项目进一步说明墙体传热系数的反演估计过程。首先需要通过调研了解建筑概况，该建筑位于黑龙江省伊春市，建成于1990年，并于2016年进行外墙及门窗热工性能提升改造。现场实测位置选在该建筑的北向外墙处，测试项目包括外墙内、外表面温度、热流密度以及室内、外空气温度等。本文采用热流计法进行墙体传热系数现场测试[10]。测试选取该建筑中北向外墙处的4个观测位置开展现场实测，测试时间为2017年1月6日～10日，各数据采集时间间隔为10分/次。测试期间共获得2 304条记录，除去少量质量不佳的数据，在其中随机选取2 000个样本数据(包含外墙内、外表面温度值和热流密度值)，形成3组样本，分别包含500、1 000和2 000个数据。经检验，3组样本数据均服从图2所示的正态分布。

图2 现场实测数据分布情况

2.2 贝叶斯估计

贝叶斯方法认为在模型参数反演过程中模型参数的后验分布决定于先验分布和观测样本数据。对于建筑墙体传热系数反演估计来说，先验分布可由设计资料或者调研结果生成，观测数据样本则被用于生成似然函数。显然，设计资料或调研结果等预估计是否准确、现场实测数据数量及准确程度均可能影响最终反演结果。接下来，将上述方法应用于反演估计，并分别分析墙体传热系数预估计信息质量以及现场实测数据数量对反演结果的影响。

2.2.1 预估计信息质量影响分析

墙体传热系数预估计信息以正态分布函数形式表达，预估计结果将以正态分布的均值和方差表示。为了分析其对反演结果的影响，将均值和方差分别设定不同数值，而后利用反演结果进行比较。以选取1 000个观测数据样本为例，将先验分布的均值和方差设定为不同数值。不同情况下墙体传热系数的反演计算结果差别很小，即后验概率分布均近似服从正态分布N(0.34,5.3×10-5)，如表1所示。结果表明：先验正态分布的均值对反演结果几乎没有影响；而方差则略有影响，先验正态分布的方差越小，则反演结果正态分布的方差也越小。

表1 不同先验分布条件下的反演结果比较

2.2.2 实测数据数量影响分析

分别计算前述所选取的不同数量(500、1 000和2 000)样本数据所对应的反演结果，具体计算条件和结果见表2。

表2 不同现场实测条件下的模型参数及反演结果比较

从表2所示的墙体传热系数反演结果可以知道：(1) 随着现场实测样本数量的增加，反演结果正态分布的均值趋于平稳，并且十分接近于观测样本所对应的正态分布均值。这一方面印证了实测数据的重要性，另一方面说明观测样本数量越大，样本数据对反演结果的影响也越大。(2) 随着所采集样本数量的增加，反演结果正态分布的方差显著减小。另外，与仅利用观测数据计算墙体传热系数相比，反演结果中正态分布的方差减小了3个数量级，大大缩小了观测误差范围。

总体而言，贝叶斯方法理论分析和实测结果均可体现预估计信息(先验分布)和观测数据样本的重要性，墙体传热系数反演结果会随观测数据样本数量的增加而逐渐稳定，先验分布对反演结果的影响逐渐减弱。但当观测数据样本数量不大时反演结果受先验分布的影响可能较大。如果现场实测条件受限，观测数据样本数量较少，也可以通过提高预估计信息的准确程度的方法提升反演估计结果质量。

3 结论

本文所提出的基于贝叶斯估计的墙体传热系数反演方法可以综合调研获取的预估计信息和现场实测所得观测数据信息，并最终以概率分布函数形式表达反演估计结果。方法利用预估计信息并强调其重要作用，预估计信息的加入可以减轻反演结果对观测数据的依赖，缩短现场检测时间，同时将更全面的反映墙体传热系数特征。

墙体传热系数反演估计将由预估计信息和现场观测数据共同决定。随着观测样本数量的增加，预估计信息的准确程度对后验结果影响将逐渐变小，而更依赖于观测样本信息。但反演估计结果与采用传统测试方法得到的结果相比，样本方差将大幅减小，使反演估计结果更加集中，可以有效弥补观测仪表精度不高的不利影响。

另外，本文所提出的方法也可以将现有墙体传热系数数据作为先验分布，而以当次的实测数据作为观测样本，模型后验分布则可以更好地反映墙体当前的传热状态。这给墙体传热系数反演估计提供了一条新途径。