基于Matlab/GUI的公交发车频率优化软件开发
2018-08-22吴小龙
唐 远 吴小龙 丁 振
(1.昆明阡陌交通工程咨询有限公司,昆明 610041 2.荆州市城市规划设计研究院,荆州 434000)
引言
行车时刻表的制定是城市公共交通企业管理的重要基础工作之一,它决定了运行时刻表、车辆调度以及分派司机等其他的日常调度工作[1]。在当前城市公交运力普遍紧张的前提下,如何经济合理地使用车辆,挖掘既有运力潜能,缓解客流拥挤是制定行车计划的目标。目前公交调度人员在安排行车计划时,主要凭借自身的工作经验和一些简单的服务性控制指标,调度计划的正确性和科学性得不到保障,不合理的作业计划将导致企业经济效益下降和社会资源浪费[2]。本文旨在从优化理论出发,利用Matlab强大的计算能力和优秀的图形可视化特性,开发界面友好和使用方便的公交发车频率优化软件[3],为企业提供科学的决策和良好的便利性。
1 模型介绍
如何根据一天中不同时刻的客流情况为每条公交线路提供合适的发车频率是提高公交服务水平的关键因素。对于发车频率的确定目前主要有最大客流方法[4]、断面客流方法[5]和考虑乘客候车时间成本、企业运营成本的多目标优化方法[6]。
1.1 最大客流方法
最大客流方法针对调查站点选取的不同分为单个站点的最大客流调查方法和基于各时段站点最大客流调查方法。对于单个站点的最大客流调查方法,调查人员全天只在一个站点进行统计,此站点为依据历史跟车调查数据确定的全日平均最大客流站点,以该站点每个时段的客流为依据,确定其发车频率,具体模型如下。

式中,F1j为确定的时段j内发车频率;Fmj为时段j内最小期望发车频率;S为站点集合(不包括末站);i*为全日最大客流站点;Pij为时段j内离开站点i的所有车辆运载乘客总数的统计学指标(平均数);Pmdj为时段j内全日最大客流站点的平均观测客流;d0j为期望的单位公交车运力;Pmd为全日最大客流站点的总客流;γj为时段j内的客流因子(0<γj≤1.0);c为单位公交车的运力。
对于基于各时段站点最大客流的调查方法,需要多名调查员分布在每个站点进行全天客流统计,统计出每个时段的最大客流站点,以该流量为依据,确定每个时段的发车频率F2j,具体模型如下。

式中,Pmj为时段j内观测到的最大客流。
1.2 断面客流方法
断面客流方法采用跟车调查获取客流数据,以载客里程指标为依据,计算每个时段内的发车频率F3j,具体模型如下。

式中,li为站点i与站点i+1之间的距离;L为线路长度;Aj为时段j内断面客流曲线下的乘客里程数。
当线路运能紧张时,可适当允许客流量超过期望拥挤度,通过设置控制参数βj来实现允许超载的线路长度,使该区间的客流量可以超出平均客流量,以此判断标准为依据,反推每个时段内的发车频率F4j,具体模型如下。

式中,Ij为时段j内断面客流Pij大于由发车频率确定的供给客流F4j·d0j的所有站点集合;βj为时段j内允许Pij大于F4j·d0j的线路长度控制参数。
1.3 多目标优化方法
公交线路调度方案的制定既要考虑企业的利益,也要考虑乘客的利益。当发车频率过高时,虽然能够满足乘客的需求,同时也增加了企业的运输成本;当发车频率过低时,虽然节约了企业的运输成本,但增加了乘客的等车时间,影响了乘客的利益,导致公交服务水平低下。通过建立同时考虑企业运营成本最小和乘客候车时间成本最小的多目标优化模型,可实现二者间利益的平衡[7][8]。
目标函数中企业运营成本包括固定成本和变动成本,由于发车次数的多少和固定成本无关,可以仅考虑变动成本部分。乘客候车时间成本为到站乘客等待时间费用。目标函数受两个条件约束,约束一为发车间隔约束,发车间隔的上限应满足交通部门规定的上限,下限应满足公交企业发车能力极限。约束二为断面需求约束,公交运营者提供的单位小时供给能力必须满足断面需求。

式中,C1为乘客候车时间成本;C2为企业运营成本;λ1为乘客单位时间费用(元/min·人);λ2为企业单位时间运营费用(元/min·辆);rij为i时段第j站的乘客平均刷卡上车人数;hi为i时段发车间隔;μ为刷卡率;Ti第i时段总时长;ti为i时段的车辆平均行驶时间;himin为i时段公交车最小发车间隔;himax为i时段公交车最大发车间隔;aij为i时段第j站的乘客平均下车人数;qi,j-1为i时段第j-1站与j站之间的断面量;Q为车辆定员;Z为发车间隔集合。
对于多目标函数求解,可通过引入权重因子,将多目标函数转换为单目标函数,具体如下。

式中α和β为多目标函数的权重因子。
2 软件设计和布局
2.1 功能设计
软件功能设计集成上述5种模型,并能够自动生成优化曲线,将5种模型的计算结果显示在曲线上。当输入实际的发车方案时,可以计算相应的评价值,便于和优化结果比较。软件同时提供公交断面客流图绘制功能,便于管理者掌握线路运行情况。所有优化结果、优化曲线和公交断面图均能够输出保存。功能结构设计如图1所示。
2.2 界面布局
界面布局包括主界面和子界面两部分,主界面根据各功能的特点进行分区设置(图2),具体划分为数据导入模块、最大客流和断面客流方法模块、多目标优化方法模块、实际方案评价模块、绘图模块和参数显示区域。子界面包括断面图绘制界面和优化曲线界面(图3),当输入数据满足要求时,各子界面会相应激活。各模块之间通过主界面和子界面的handles句柄结构数组、UserData属性实现不同控件间的数据传递和存储[9]。
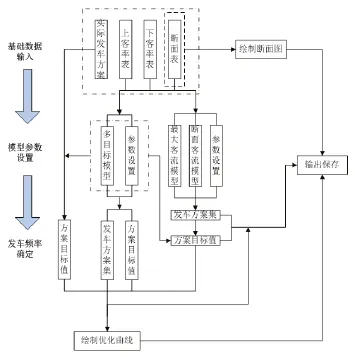
图1 功能结构设计

图2 主界面布局

图3 断面图绘制和优化曲线绘制界面布局
2.3 优化程序设计
对于多目标优化而言,由于发车间隔的确定总是在一个固定区间内,即发车间隔的最大值和最小值是可以确定的,同时,根据发车特点,潜在解集总是离散的,故可行解的确定可采用枚举法先完成潜在解的生成,再剔除不满足约束条件的解,具体流程如图4所示。

图4 可行解生成流程
潜在解是由不同时段的发车间隔组成的一维数组,假设划分时段数为n,则潜在解可表示为I=[I1,I2,…, In]。程序设计难点在于如何根据不同的划分时段n生成一个维度为n的潜在解,为了解决此问题,可将时段n作为一个参数传入自定义函数内,该函数根据参数n返回一个n层嵌套循环代码的字符串,再采用eval()函数执行字符串代码完成潜在解的生成,具体如下。
for i=1:seqnum %生成字符串代码
tmp_strfor=sprintf('for %s=%d:%d ',iter{i},hdw_interval(i,1),hdw_interval(i,2));
str_for=[str_for,tmp_strfor];
str_end=[str_end,tmp_end];
tmp_solution=[iter{i},' ']; %字符串表达式
eval_solution=[eval_solution,tmp_solution];
end
str=[str_for,sprintf(' '),'tmp_solution=[',eval_solution,'];',sprintf(' '),'potential_solution=[pot_ential_solution;tmp_solution];',sprintf(' '),'str_end]; %字符串代码生成
eval(str); %调用eval()执行字符串代码
潜在解集生成后,将不满足约束条件的解排除,剩余的解集就是可行解集,具体如下。
function feasible_solution=FeasibleSolutionBasedSectio
n(handles,potential_solution,r,a,T,miu,Q)
% potential_solution潜在解集
% r 分时段分站点刷卡上车率
% a分时段分站点下客率
% T 分时段的时长数组
% miu IC卡率
% Q 车辆定员
% feasible_solution 可行解
r=r/miu;
q=SectionVolume(r,a); % 断面率
n=size(potential_solution,1);
num_section=size(q,2);
Tmatirx=repmat(T,1,num_section);
feasible_solution=[];
for i=1:n
h_mat=repmat(potential_solution(i,:)',1,num_section);
constrain=q.*h_mat;
count=0;
for j=1:numel(constrain)
if constrain(j)>=0*Q && constrain(j)<=1*Q
count=count+1;
else
break;
end
end
if count==numel(constrain)
feasible_solution=[feasible_solution;potential_solution(i,:)];
end
end
为便于不同模型计算出的方案进行比较,将多目标优化方法的目标函数作为实际发车方案、最大客流方法和断面客流方法的目标值计算依据,根据不同方案的计算结果,进行升序排序,绘制优化曲线。
3 案例应用
本文以昆明市44路车回程方向的跟车调查数据作为研究对象,进行发车间隔优化分析。44路回程起始于海埂公园站,沿线经过滇池路和环城南路(图5),途经19个站点到达昆明站,全程采用一票制,是南市区重要的公交客流通道。
根据客流时间分布特征,将时段划分为7个,各时段的时长、最小发车间隔、最大发车间隔、发车频率、发车间隔和平均行程等统计指标见表1。

图5 路回程方向线路示意图
分时段各站点的上客率、下客率和断面量见表2、表3、表4。
参考昆明市经济水平和基本工资水平,乘客等车单位时间成本取0.554元/min·人,企业单位运营成本取1.7元/min·辆,因为是跟车调查,刷卡率取100%,乘客权重和企业权重均为0.5,车辆定员为80人,将参数和基础数据导入软件,得到优化结果如图6所示。
表5为不同方式优化结果对比,从优化结果来看,多目标优化方案计算的目标值为15347.7元,为全局最优,而实际方案次之,其目标值为15608.3元,二者相差260.6元,由此看出公交调度者凭借自己丰富的工作经验,其制定的发车方案已经很接近最优值,但相比多目标优化结果来说仍有一定的优化空间。而方法1~方法4计算的发车方案目标值较大,主要是因为其确定的依据是以满足乘客的乘车需求而考虑,牺牲了部分企业利益。

表2 分时段站点上客率表(人/min)
4 总结
基于目前主要的公交发车频率确定方法构建Matlab/GUI框架,实现了模型算法的集成化、可视化和交互式功能。软件提供优化曲线绘制功能和断面图绘制功能,通过对各方案进行指标量化,为用户提供科学的决策依据。最后文章通过昆明44跟车调查数据,展示了软件的优化功能,结果证明软件计算结果正确,各项功能达到设计要求,对各专业人员运用Matlab语言快速开发出具备强大计算功能的专业应用软件具有重要意义。

表3 分时段站点下客率表(人/min)

图6 44路优化曲线图

表4 分时段公交断面量表
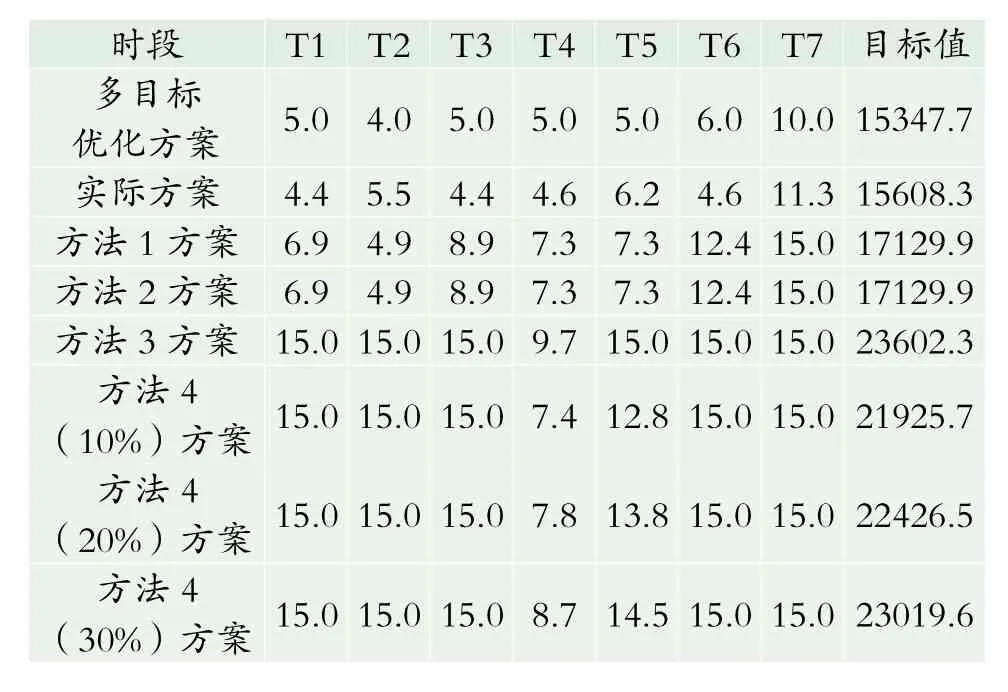
表5 不同方法优化结果对比表
