基于BP神经网络学习率优化的研究

赵建民， 王雨萌

(东北石油大学 计算机与信息技术学院， 大庆 163318)

0 引言

1943年，Warren Mc Culloch 和 Walter Pitts 提出了神经网络层次结构模型[1]，确立为神经网络的计算模型理论，从而为机器学习的发展奠定了基础。1950年“人工智能之父”图灵发提出了著名的“图灵测试”，使人工智能成为了计算机科学领域一个重要的研究课题[2]。

人工智能已成为全球新一轮科技革命和产业变革的着力点[3]，其推广和应用获得了极大的成功，并逐渐成为一种极其重要的工程技术[4]。随着人工智能技术的日益成熟和不断深入，研究人员发现神经网络愈发体现出其优越的性能，神经网络是人工智能发展中所使用的重要方法，也是当前类脑智能研究中的有效工具[5]。而BP神经网络(Back Propagation Neural Networks，BPNN)[6]则是应用普及程度最高的一项神经网络内容[7-8]，BP神经网络已广泛应用于非线性建摸、函数逼近、系统辨识等方面[9]。

本文将对标准的BP神经网络算法进行改进，通过验证异或问题并结合模式识别[10]中的手写模式识别[11]，将变化学习率应用于经典的BP神经网络，用以解决固定学习率在训练模型时所出现的易越过全局极小值点、模型收敛速度慢[12]的问题。

2 BP神经网络

BP神经网络是一种信号由正向传播，误差按逆传播算法训练的多层前馈神经网络，BP神经网络具有非线性映射能力强，容错能力强，泛化能力强等优点。标准的BP神经网络模型包含三层，分别是输入层、隐藏层和输出层.在正向传播过程中，输入样本从输入层传入，传向输出层。中间过程为，输入信号经隐层逐层传递，根据输出层的实际输出是否与期望输出不符的判别条件，转入误差的反向传播[13]，其目的为将误差分摊给各层所有单元，用各层单元的误差信号修正各单元的权值，BP神经网络模型如图1所示。

1) 定义BP训练所需函数：

损失函数，定义为式(1)。

(1)

其中，E表示损失函数，l表示样本总数，Yk表示输出值，Dk表示输出值。

激活函数，定义为式(2)。

图1 BP神经网络模型

(2)

激活函数的作用是将每一层的输出转换成为非线性元素，本文实验选择的是传统的三层BP神经网络，激活函数选取的是Sigmoid激活函数[14]，Sigmoid函数的优点在于输出的取值范围为(0,1)，故函数可以将每层加权后的输出映射到(0,1)的区间，可以很容易的抑制相差比较大的误差，并且在神经网络反向传播误差优化参数时，需要对激活函数进行求导，Sigmoid函数导数可以用自身函数表达式来表示，Sigmoid函数导数表达式，为式(3)。

f′(x)=f(x)(1-f(x))

(3)

Sigmoid函数图像如图2所示。

图2 Sigmoid函数

2) BP神经网络定义如下：

输入层的输入向量为：X=(X1,X2,… ,Xn)；

隐藏层输出向量为：H=(H1,H2,… ,Hm);

输出层输出向量为：Y=(Y1,Y2,… ,Yl)；

期望输出向量为：D=(D1,D2,… ,Dl)；

输入层到隐藏层权值矩阵为：V=(V1,V2,…，Vj，…,Vm)；

隐藏层到输出层权值矩阵为：W=(W1,W2,…，Wk，…,Wl)。

3) 正向传播输入信号过程

隐藏层输入为式(4)—式(7)。

(i=1,2,…，n)

(4)

隐藏层输出为：

Hj=f(netj) (j=1,2,…，m)

(5)

输出层输入为：

(j=1,2,…，m)

(6)

输出层输出为：

Yk=f(netk) (k=1,2,…，l)

(7)

4) 误差的反向传播过程

输出层损失函数为式(8)。

(8)

将损失函数反向传播回隐藏层为式(9)。

(9)

将误差反向传播回输入层为式(10)。

(10)

误差对输出层各神经元权值的偏导数为式(11)。

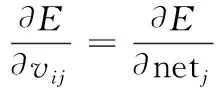
(11)

误差对隐藏层各神经元权值的偏导数为式(12)。

(12)

设置学习率为η，对隐藏层到输出层权重进行更新为式(13)、(14)。

(13)

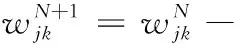
(14)

对输入层到隐藏层权重进行更新为式(15)、(16)。

(15)

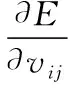
(16)

3 BP神经网络算法优化

神经网络的性能主要取决于三个因素：一是用于训练神经网络的样本的特征选择方法，二是神经网络的优化算法，最后是神经网络隐层节点的选择方法[15]。

本文选取第二种因素神经网络的优化算法对BP神经网络进行优化改进，BP神经网络的核心在于计算前向传播最后的输出结果与预期输出的误差的偏导数[16]，利用这个偏导数和隐藏层进行加权求和，一层层向后传播，直到传到输入层，最后利用每个节点求出的偏导数更新权重。而使用梯度下降法的实质，是不断更新参数，对于步长的选取通常可以决定神经网络的收敛速度以及结果的准确率，步长选取过大，模型易越过全局极小值点，步长选取过小，模型收敛速度慢，相比于固定学习率，变化学习率在模型训练时体现出其极大的优势。

在模型训练中,当η大于0.2且为固定值时,从第一次迭代起误差函数值就会几乎不下降 ,且其值都很相近，原因为随机权值与系统真实权值相差较大，由此随机权得出的误差值必然较大[17]。

本文针对BP神经网络算法提出一种改进的变化学习率为式(17)。

(17)

其中Δw为误差对各层神经元权值的偏导数。

相比于固定学习率，变化学习率不仅可以加快模型收敛速度，更可以随着每次迭代的损失函数调整步长，有效的预防了模型发散的问题，将优化的学习率用于BP神经网络的步骤如下：

对隐藏层到输出层进行权重更新为式(18)。

(18)

对输入层到隐藏层进行权重更新为式(19)。

(19)

4 实验验证

4.1 实验环境搭建

本文采用Python编程技术，集成开发环境采用Anaconda3中的juypter notebook，Anaconda是一个主要面向科学计算的Python开源发行版本，Anaconda集成了计算、可视化和程序设计等强大的功能，预装了大量的Python第三方库，例如Numpy、Scipy、Matplotlib等，为本文的实验提供了便利。

4.2 实验

本实验的目的是为了验证改进的变化学习率运用在BP神经网络算法的有效性。本文设计了两个实验来进行验证，实验一是利用BP神经网络解决异或问题的对比实验，实验二是利用Python第三方模块sklearn中的手写数字识别数据集对固定学习率和本文提出变化学习率的对比实验。

4.2.1 实验一

实验一运用三层BP神经网络实现异或问题来证明本算法的有效性。

首先运用传统的固定学习率的三层神经网络进行实验，每迭代五百次记录一次误差信息，实验结果如下：

time:1500 Error:0.458404517166

time:2000 Error:0.360931277441

time:2500 Error:0.229372589968

time:3000 Error:0.155475012087

time:3500 Error:0.118675634533

time:4000 Error:0.0975626246316

time:4500 Error:0.0839069786167

time:5000 Error:0.0743082823057

time:5500 Error:0.0671542277731

time:6000 Error:0.0615890525893

time:6500 Error:0.0571173479187

time:7000 Error:0.0534323355973

time:7500 Error:0.0503336484737

time:8000 Error:0.0476846679439

time:8500 Error:0.0453888887144

从实验结果可以看出在训练BP神经网络时学习率设置为固定学习率时，迭代1500次时训练的误差约为是45.84%，而在迭代8500次误差达到4.53%。

进行对比试验，对比实验的神经网络中的其他参数不变，步长设置为本文提出的优化后的变化学习率，实验结果如下：

time:1500 Error:0.160769081427

time:2000 Error:0.096897464958

time:2500 Error:0.0728406727105

time:3000 Error:0.0599997421748

time:3500 Error:0.0518647863821

time:4000 Error:0.0461737143615

time:4500 Error:0.0419278562032

time:5000 Error:0.0386145218412

time:5500 Error:0.0359417347153

time:6000 Error:0.0337301230737

time:6500 Error:0.0318629342354

time:7000 Error:0.030260631329

time:7500 Error:0.0288669969007

time:8000 Error:0.0276410690144

time:8500 Error:0.0265522297624

由实验结果可以看出，在对学习率进行优化后，迭代1500次时训练的误差就已经降低到16.07%，而在迭代8500次误差降低到2.66%，模型的收敛速度有了明显的提高。

4.2.2 实验二

本文同时进行手写识别实验证明改进学习率后的BP神经网络的泛化能力，此次实验隐藏层定义了六十个神经元，所选用数据集来自sklearn模块的手写识别数据集。

同样首先采用固定学习率的BP神经网络进行训练，每迭代五百次记录数据一次训练结果的准确率，并且手写识别实验采用数据分批训练的方式在不影响模型准确率的前提下提升训练速度，实验结果如下：

time:11500 acc:0.848888888889

time:12000 acc:0.851111111111

time:12500 acc:0.851111111111

time:13000 acc:0.853333333333

time:13500 acc:0.853333333333

time:14000 acc:0.857777777778

time:14500 acc:0.857777777778

time:15000 acc:0.882222222222

time:15500 acc:0.966666666667

time:16000 acc:0.966666666667

time:16500 acc:0.971111111111

time:17000 acc:0.962222222222

time:17500 acc:0.964444444444

time:18000 acc:0.973333333333

time:18500 acc:0.971111111111

time:19000 acc:0.975555555556

time:19500 acc:0.975555555556

time:20000 acc:0.975555555556

从实验结果可以看出利用BP神经网络识别手写数字时，学习率未优化时，迭代11500次时训练的准确率约为84.89%，而在迭代20000次训练的准确率才达到97.56%，模型收敛速度较慢。

将优化后的变化学习率用在BP神经网络识别手写数字实验时，实验结果如下：

time:5500 acc:0.957777777778

time:6000 acc:0.951111111111

time:6500 acc:0.962222222222

time:7000 acc:0.968888888889

time:7500 acc:0.96

time:8000 acc:0.964444444444

time:8500 acc:0.962222222222

time:9000 acc:0.962222222222

time:9500 acc:0.968888888889

time:10000 acc:0.966666666667

time:10500 acc:0.964444444444

time:11000 acc:0.982222222222

从实验结果可以看出使用优化后的变化学习率未优化时，在迭代5500次时训练的准确率就已经达到95.78%，模型的收敛速度相较以及准确率使用固定学习率的BP神经网络有了较大幅度的提升。

5 总结

本文运用经典的BP神经网络，对其传统的固定学习率进行优化改进，并通过优化后的神经网络解决异域问题以及手写模式识别两个实验，证明了改进算法确实对模型的收敛速度以及准确度有了一定程度的提高，证明了改进后算法的有效性。