基于饱和与非饱和土力学的边坡稳定算例分析

杨安玉

(1.水利部农村电气化研究所，浙江 杭州 310012；2.水利部农村水电工程技术研究中心，浙江 杭州 310012；3.南京水利科学研究院，江苏 南京 210029)

1 概 述

土是由固体颗粒和液、气三相组成的松软集合体。工程研究中常将土简化由固、液两种物质构成，然而实际工程中所遇的情况多是以三相状态出现。土力学上将固、液两相称之为饱和土力学，与之对应，将土作为固、液、气三相物质进行研究称之为非饱和土力学。当前饱和土力学已形成了一套完善、独立的理论体系，通过合理的简化假设，也广泛有效的运用于各类工程研究中。但是，对于某些特殊区域或特殊性质的土，类似的简化假设将造成研究理论的失误，从而危及工程安全。

非饱和土力学的研究始于20世纪30年代，由于非饱和土体的复杂性，使得理论研究进展缓慢。到50年代，由于太沙基的有效应力公式在描述饱和土性状方面取得的巨大成功，使研究者将建立非饱和土有效应力公式作为目标。1959年，Bishop率先提出了分别考虑孔隙气体和孔隙水对强度影响的非饱和土的有效应力公式，但是公式不能说明非饱和土在湿化过程中的湿陷现象。此后，Coleman、Bishop、Blight提出了用两个独立的应力变量—静应力和基质吸力描述非饱和土的强度和变形。Fredlund和Morgenstem提出了零位试验，验证了采用这两个独立变量描述非饱和土的强度和变形的正确性。自此，用双应力变量作为有效应力的研究得到了迅速发展并应用于多种工程研究。

2 关于边坡工程的研究

2.1 边坡稳定分析概述

边坡抗滑稳定分析是土力学研究的重要课题之一。简化Bishop法是常用的分析方法，该方法是建立在静力学基础上的力系平衡理论，计算中所采用的抗剪强度采用饱和土的试验指标。

简化Bishop法是圆弧条法的一种，将边坡滑动面假定为圆弧面，同时将滑动土体竖向分成若干土条，分别求解作用与各土条上的力对圆心的滑动力矩和抗滑力矩，并将滑动面上的抗剪强度与实际产生的剪应力之比定义为边坡稳定安全系数，公式为：

(1)

(2)

式中，c为粘聚力；φ为内摩擦角；u为滑面上孔隙水压力；w为单个土体的自重；α为土条至圆心直线与竖向的夹角；b为单个土条的宽度；i为土条的序号。

现实中，边坡易受雨水或地下水反复作用而处于非饱和状态，采用上式分析这种状况下的边坡时将存在较大的误差。针对这种情况，可以考虑将非饱和土的总粘聚力c=c′+(uα-uw)tanφ′和ui=uα代入式(2)，同时对于土坡有uα=0，有式：

(3)

式中，R为圆弧半径；uw为孔隙水压力；l为土条的长度；Q为单个土条中水重。

2.2 算例

某均质粘土质边坡高25 m，坡度1∶2，土的重度γ=20 kN/m3,内摩擦角φ=25°，粘聚力c=10 kPa，假定滑动圆弧半径R=50 m。假设当边坡受降雨影响处于非饱和状态时，粘聚力c′=9 kPa，内摩擦角φ′=20°，孔隙水压力u=1 kPa，土的水重度γ′=2 kN/m3。

采用简化Bishop法求解此边坡稳定系数Fs(见图1)，将滑动土体分为宽5 m的土条，共12块。

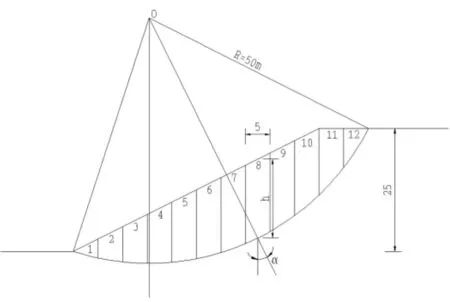
图1边坡稳定计算示意

(1)基于饱和土力学理论进行稳定计算(见表1)。

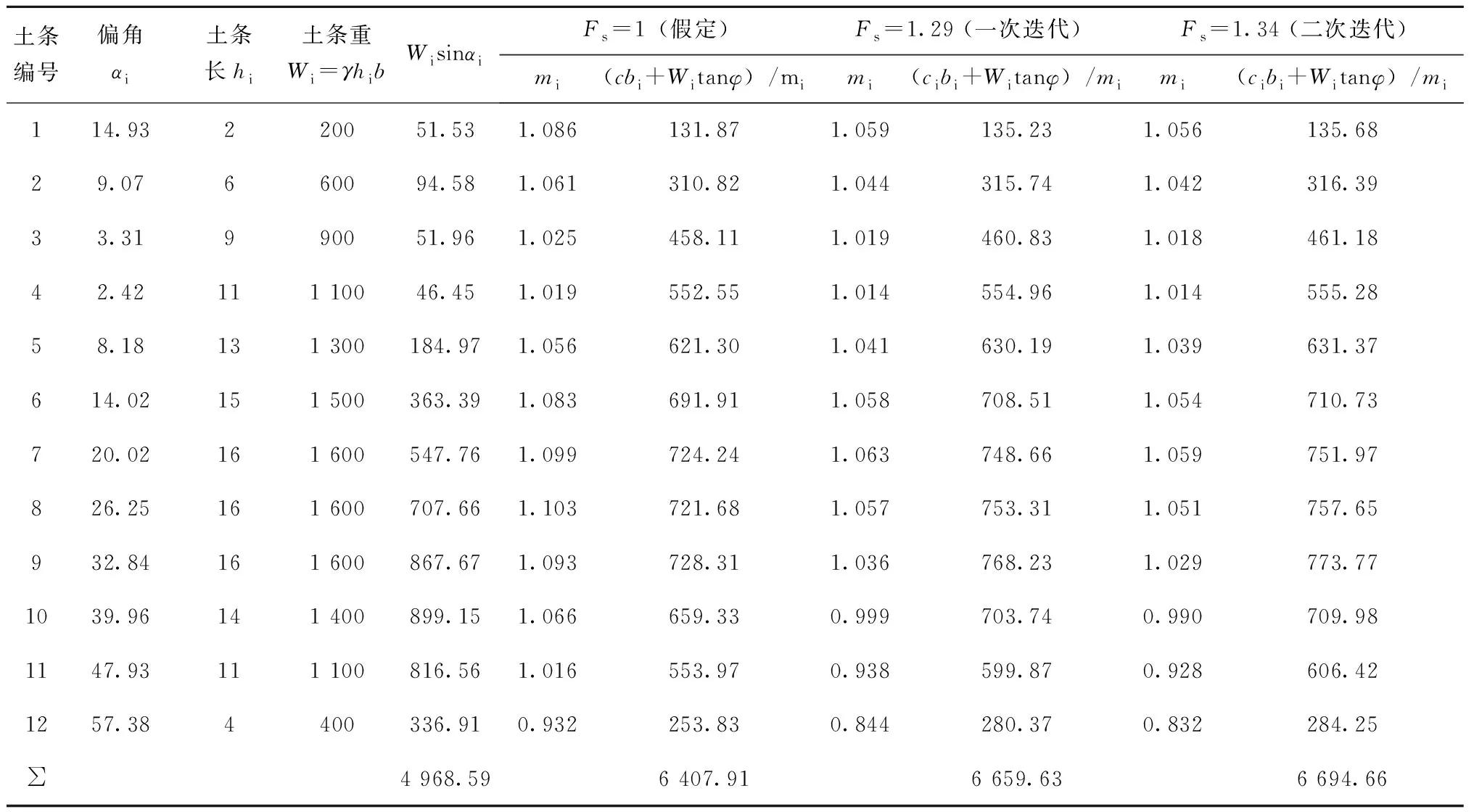
表1 边坡稳定计算(不考虑孔隙水压)

第三次假定Fs=1.07，求得：

(4)

故求得稳定安全系数Fs=1.34。

(2)基于非饱和土力学理论进行稳定计算(见表2)。

表2 边坡稳定计算(考虑孔隙水压)

第四次假定Fs=1.07，求得：

(5)

故求得稳定安全系数Fs=0.94。

根据对比计算结果可知，将边坡视作非饱和土状态考虑孔隙水压力时，求解安全系数更低，即相较于饱和土力学理论计算结果，实际情况是边坡处于更危险状态。

3 结 语

对于明显处于非饱和状态的土质边坡工程进行稳定分析时，应采用非饱和土指标进行计算；且今后当获取非饱和土指标更为简捷准确时，对于任意状态下的边坡工程都应当采用非饱和土指标进行分析。