云环境下矩阵乘法外包计算方案

聂恒太，王少辉

(1.南京邮电大学 计算机学院，江苏 南京 210003；2.江苏省无线传感网高技术研究重点实验室，江苏 南京 210003;3.江苏省大数据安全与智能处理重点实验室，江苏 南京 210023)

1 概 述

云计算作为一种新的计算模式，允许公司、组织和个人从服务提供商租用计算和云存储资源[1-2]在云服务器完成对本地的计算任务。介于云计算强大的计算能力，计算能力薄弱的客户端或设备可以外包它们繁重的计算任务和数据(例如，大矩阵乘法或代数计算)给云服务器计算，尽可能减少用户端计算成本。近年来，外包计算[3-9]受到广泛关注，已经成为一个热门的研究课题。

与外包计算迅速发展相对应的是这种新的计算模型带来的两个主要安全挑战。用户面临的第一个挑战是数据隐私。外包计算的输入和输出数据通常包含用户不想暴露在云服务器上的敏感信息，而云服务通常假定不完全可信。因此，需要对原始数据和计算结果采取诸如数据伪装、问题转化和加密等安全措施，以防止用户的信息泄露。第二个挑战是计算结果的正确性验证。一般除了软件错误或硬件故障外，云服务器可能不按照外包方案的具体程序执行，比如云服务器直接选择难以区分的无效结果返回给用户。所以，用户必须具备进行结果正确性验证或者委托第三方验证机构进行结果正确性验证的能力。

大矩阵运算[10-13]已被广泛应用于当前的计算研究、电子应用和3D图像处理等领域。因此，如何把高复杂度的矩阵相关运算安全外包给云服务器进行计算是外包计算领域的一个重要内容。矩阵相关算法主要包括矩阵乘法、矩阵求逆和线性方程组求解等，已经有了大量的研究成果。

Li Hongwei等[14]在2015年提出了一种可公开验证的矩阵乘法外包算法，算法中采用了伪随机函数方法，在得到计算结果的同时提高了算法效率，但是该方案的验证算法过于复杂，用户端计算量太大，无法达到实际应用的效果。2013年，Lei Xinyu等[15]提出了一种大规模矩阵求逆的外包计算方案，该方案利用置换矩阵和稀疏矩阵成功地保护了用户的输入和输出隐私，但是用户在整个算法执行过程中计算负载过高，也无法在实际中使用。2013年，Wang Cong等[16]利用数学中的迭代法设计了一种新型的计算大规模线性方程的方法。但是，初始迭代向量的选择随机性太大，具有很大的偶然性，而且用户要与云端进行多次的交互致使用户端的时间开销依然很大，所以很难使用。

2016年，Zhang Jian等[17]提出了一种针对大规模线性方程组的外包方案，通过特殊的置换函数和系数矩阵保护原有矩阵不被窃取，但是同样存在着用户端计算负载过高的问题。不管如何设计外包方案，如果用户端在整个协议执行过程中计算所消耗的时间接近或超过了自己直接解决问题所需的时间，那么这种外包方案是没有多大意义的。

2016年，Gang Sheng等提出了一种矩阵乘法外包方案MD-VCMatrix[18]，该方案主要侧重于验证效率的改进，未对输入和输出信息的隐私性进行保护。文中在MD-VCMatrix方案的基础上考虑数据隐私保护，提出了一个新的矩阵乘法外包方案，并在执行效率、算法的隐私性保护和可验证性等方面与其他方案进行了综合比较。

2 问题描述

2.1 系统模型

如图1所示，可公开验证的矩阵乘法计算外包方案由三方协作完成：外包用户、云服务器和验证方。外包用户一般计算或存储资源受限，将矩阵和向量的乘法运算外包给云服务器。云服务器利用其强大的计算能力执行来自外包用户的外包计算业务。而验证方主要验证云服务器的临时结果是否正确。如果结果正确，将临时结果返回给用户。

图1 系统模型

该方案包括如下五个子算法：

(1)KeyGen(1λ)→PK：以安全参数λ作为输入，算法输出公共参数PK。

(2)ProbGen(M,x)→(BE,VE)：用户对原始矩阵M和原始向量x进行盲化处理，将盲化结果BE发送给云服务器，验证数据VE发送给验证方。

(3)Compute(BE)→(y',v)：云服务器计算得到临时结果y'和验证信息v，这两个信息都会发送给验证方。

(4)Verify(VE,y',v)→true/false：验证方接收到数据y'和v，利用VE，验证方验证结果的正确性，若正确则将结果发送给用户，否则提示用户结果有误。

(5)Solve(y')→y：用户接收到验证方发送的信息y'，计算出矩阵运算的结果M·x。

2.2 攻击模型

外包系统模型所面临的安全威胁主要来自于云服务器的恶意行为。一般来说，有两种常见的外包模型：半诚实模型和恶意模型[19]。在半诚实模型中，云服务器会忠实地执行协议流程，但其还会侦听并分析协议中传输的信息，进而得到诸如用户的输入输出等敏感信息。而在恶意模型中，云服务器是主动攻击者，其很有可能会因为软硬件错误或者商业利益的诱导等原因故意发送一个难以区分的无效结果给用户，同时希望恶意行为不被检测出来。因此，外包协议必须能够进行结果验证并具有高可验证性。文中采用恶意模型即云服务器被假定为恶意的服务器，而验证方认定为诚实服务器。

设计目标主要包括以下几点：

(1)隐私性：在执行新方案时，云服务器在协议交互的过程中无法获取到用户的输入和输出信息。

(2)可验证性：云服务器的计算结果必须通过验证方验证成功，否则不会发送给用户。错误结果可以通过验证的概率极低，文中方案可验证概率接近于1。

(3)效率：无论执行效率和内在需求的要求都要尽可能低，以减少客户端的计算负担。

2.3 数学定义

定义1(非对称双线性对):设G1、G2和GT是阶为大素数q的乘法循环群，若满足以下条件，则称e:G1×G2→GT是一个非对称双线性映射。

(1)双线性：对于任意的a,b∈Zq,g∈G1和h∈G2,e(ga,hb)=e(g,h)ab。

(2)非退化性：对于任意的g∈G1，若h∈G2，e(g,h)=1，g=1。

(3)可计算性：对于g∈G1,h∈G2，存在有效算法计算得出e(g,h)。

3 新方案设计

新方案的每个子算法依次构建如下：

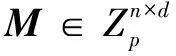
m=r·M'

x'=A2·x

VKx'=e(ρx',g2)

w=(w1,w2,…,wd)

计算结束后，用户将M'、w和x'发送给云服务器，而将VKπ′发送给验证方。

Verify(VKx'，PK，y'，v):验证方验证下面等式是否成立:

Solve(y')→y:若用户接收到验证方发来的信息y'，则通过以下公式解密出真正的结果y：

4 方案分析

4.1 正确性分析

定理1：如果数据PKM'、VKx′、y'和v被正确计算，那么文中的验证方案是正确的。

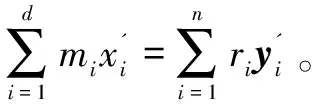
由上面的推导过程可知，文中的验证方案正确。

定理2:如果协议正确执行，那么用户计算的y是矩阵乘法运算的正确结果。

证明：根据KenGen，ProbGen和Compute三个阶段的算法，可知：

可以得出：

从而有：

因此，只要协议正确执行，计算结果y是矩阵乘法运算的正确结果。

4.2 安全性分析

(1)输入信息的隐私性。

(2)输出信息的隐私性。

(3)公开验证的安全。

4.3 性能分析

文中协议涉及的运算主要包括整数的加减乘运算、双线性运算和模幂运算。由于整数的加减运算复杂度较低，在计算算法效率方面只考虑乘法运算、双线性运算和模幂运算。文中用BC表示双线性运算，EC表示模幂运算，MC表示乘法运算。下面将文中算法与现有算法在执行效率、可验证概率进行比较，由于云端计算能力强，速度快，只考虑用户的计算负载。结果如表1所示。

从表1可以看出，文中算法的可验证概率远高于Lei Xinyu等和Fu Shaojing等提出算法的可验证概率，但是效率低于后者；文中算法的效率高于Li Hongwei等提出的算法，而且可验证概率接近于1。

表1 算法比较

5 结束语

提出了一种可验证的安全有效的矩阵乘法外包计算方案，在提供高可验证性的同时，能够提供运算输入输出信息的隐私性保护。然而，由于在方案中考虑到了隐私性保护，在一定程度上增加了外包用户的算法执行开销，但这种开销被控制在可接受的范围内。与现存方案相比，在执行效率或可验证概率等方面都有较好的表现。

下一步，将考虑尽量减少用户的计算量，达到高效和高可验证概率并存的目的，同时考虑在多服务器上进行运算外包。