基于去冗余的MIMO雷达多维角度分阶段估计

陈 丽 刘庆华

(桂林电子科技大学无线宽带通信与信号处理省部重点实验室,广西桂林 541004)

1 引言

MIMO雷达是一种比较新的雷达概念,具有诸多优点和广泛应用领域,其潜在优势近年来已引起了人们的广泛关注[1-3]。

目前,针对MIMO雷达系统中目标收发角度的估计方法大多数都是在高斯白噪声假设条件下实现,但高斯白噪声假设下的收发角度估计算法在实际环境中性能将急剧下降[4],又因双基地MIMO雷达同时估计离开角(DOD, direction of department)和到达角[5](DOA, direction of arrival),需要考虑参数的配对问题,且这些算法研究一般都是在均匀线阵中进行,仅能估计目标的二维角度,难以达到精确定位的目的。对此,文献[6]使用基于累积量的稀疏表示方法,得到色噪声背景中目标的角度信息,但其仅在单基地MIMO雷达中进行,只能估计出一维信息。文献[7]在色噪声环境中应用传统MUSIC估计DOA、DOD,但是其在均匀线性阵列结构中完成,仅得到目标的二维角度信息。文献[8]通过两次使用ESPRIT算法,达到估计参数自动配对的目的,但是是在高斯白噪声条件下实现的。文献[9]通过酉双分辨ESPRIT方法求得DOA、DOD估计值,同时参数能实现自动配对。对于实际应用,L型的阵列结构可得到目标的多维角度信息,达到更精确的目标定位目的。文献[10]根据传播算子的旋转不变性,估计二维离开角和二维到达角,参数无需额外配对,但是低信噪比时性能较差。文献[11]在L型阵列结构的双基地MIMO雷达系统中两次使用ESPRIT,可得目标的四维角度信息,参数能自动配对,算法性能相对较好。文献[6]、[7]所提算法均能在色噪声背景条件下实现目标角度估计,但由于算法分别是在单基地MIMO雷达系统和均匀线性阵列结构的双基地MIMO雷达系统中实现,仅能得到目标的一维、二维角度信息,针对这问题,本文应用L型阵列结构的双基地MIMO雷达作为算法实现系统,提出基于四阶累积量的算法,以实现色噪声背景条件下目标的四维角度估计,同时,针对本文所用系统及估计方法,提出了分段部分去冗余的方法,改善了算法复杂度。文献[8-9]所提算法均实现了参数的自动配对,但都是在均匀线性阵列结构的双基地MIMO雷达系统中实现,且算法是在白噪声背景条件下进行研究,无法实现目标的多维角度信息估计,同时在色噪声背景条件下,算法性能将急剧下降。本文首先利用ESPRIT算法估计二维DOA,然后利用MUSIC算法估计二维DOD,可实现二维DOA、二维DOD各自的内部参数自动配对,又因DOD的求解依赖于DOA,所以DOA、DOD之间也可实现配对,从而实现目标四维角度估计以及估计参数的自动配对,与此同时,本文算法在色噪声环境下实现。文献[10-11]所提算法估计了目标的四维角度,但是仅研究高斯白噪声的情况,并且收发角度的估计性能不相关。本文利用基于四阶累积量的分步估计方法,实现色噪声背景条件下目标的四维角度联合估计。

本文为在色噪声背景中获得MIMO雷达目标的多维角度信息及降低计算复杂度,利用四阶累积量对色噪声的不敏感性及其结构特点,提出基于去冗余的FOC-ESPRIT-MUSIC多维角度分阶段估计算法。针对所提算法,首先,由接收阵列导向矢量估计值通过交换矩阵得到发射阵列导向矢量,利用该发射阵列导向矢量重构DOD估计对应的重构信号,然后,对MIMO雷达的接收数据和重构信号构造四阶累积量矩阵,并使用分段部分去冗余的方法对累积量矩阵进行处理。最后,为避免四维谱峰搜索,分别利用FOC-ESPRIT、FOC-MUSIC算法求解目标的二维DOA、DOD。对于DOA估计,使用FOC-ESPRIT算法实现,首先通过特征分解方法求解相应信号子空间,再根据信号子空间的旋转不变性,估计出DOA方位角和仰角；对于DOD估计,使用FOC-MUSIC算法实现,首先通过特征值分解方法求解相应噪声子空间,再写出相应谱函数,最后将DOA方位角和仰角的估计值带入其中,并通过二维谱峰搜索估计出DOD方位角和仰角。理论分析表明,所提算法实现了目标的四维角度联合估计,有效抑制高斯噪声影响,免除高维谱峰搜索,又因SEG_INC_RR方法的使用,再次改善了算法复杂度。

2 信号模型

考虑双基地MIMO雷达系统内使用L型阵列结构。假设发射端的L型阵列在x轴和y轴上均有M个阵元,接收端的L型阵列在x轴和y轴上均有N个阵元,并且阵元间隔均为d=λ/ 2。发射端发射正交脉冲信号S=[s1,s2,...,s2M-1]T(S∈C(2M-1)×Ls),快拍数为Ls,假设有K个不相关点目标位于远场,系统结构如图1所示。

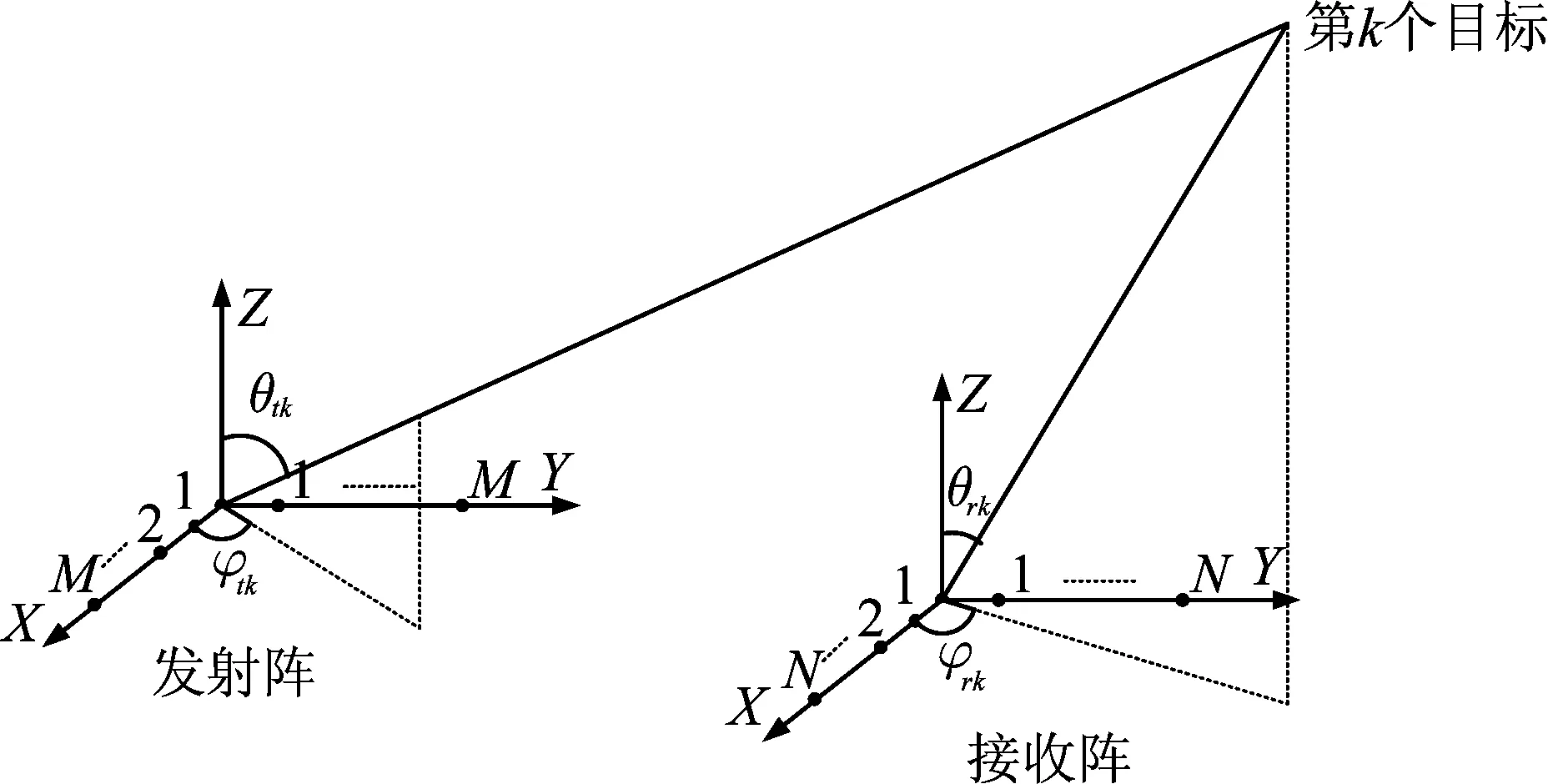
图1 L型阵列系统结构图

定义第k(k=1,2,...,K)个目标的方位为(θrk,φrk,θtk,φtk),其中,DOA仰角和DOA方位角分别是θrk和φrk,DOD仰角和DOD方位角分别是θtk和φtk,则第k个目标对应收、发阵列的方向矢量分别为：

ar(θrk,φrk)=[1,e-jπcos(φrk)sin(θrk),…,e-jπ(N-1)cos(φrk)sin(θrk),

e-jπsin(φrk)sin(θrk),…,e-jπ(N-1)sin(φrk)sin(θrk)]T

at(θtk,φtk)=[1,e-jπcos(φtk)sin(θtk),…,e-jπ(M-1)cos(φtk)sin(θtk),

e-jπsin(φtk)sin(θtk),…,e-jπ(M-1)sin(φtk)sin(θtk)]T

在第q(q=1,2,...,Q)个发射脉冲下,定义βq=diag(η1,q,η2,q,...,ηK,q),其中,ηk,q为目标回波的复幅度,则接收端接收到的信号为

(1)

式中,信号Yq∈C(2N-1)×Ls,Ar(Ar=[ar(θr1,φr1),ar(θr2,φr2),...,ar(θrK,φrK)])为接收方向矩阵,At(At=[at(θt1,φt1),at(θt2,φt2),...,at(θtK,φtK)])为发射方向矩阵；Wq表示加性复高斯色噪声,diag(·)表示对角化操作。

(2)

式中,Xq∈C(2M-1)(2N-1)×1,定义A=Ar∘At为收、发阵列的联合方向矩阵,则A=[ar(θr1,φr1)⊗at(θt1,φt1),ar(θr2,φr2)⊗at(θt2,φt2),...,ar(θrK,φrK)⊗at(θtK,φtK)],其中,‘⊗’表示Kronecker积运算,wq是噪声项。

方向阵A也可以表示为

(3)

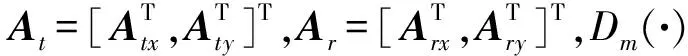
Φrx=diag(exp(-jπcos(φr1)sin(θr1)),…,

exp(-jπcos(φrk)sin(θrk)))

Φry=diag(exp(-jπsin(φr1)sin(θr1)),…,

exp(-jπsin(φrk)sin(θrk)))

3 四阶累积量的构造及去冗余

3.1 四阶累积量矩阵

对于复随机过程,四阶累积量的定义有多种方式,本文采用以下方式来定义四阶累积量：

1≤K1,K2,K3,K4≤(2M-1)(2N-1)

(4)

R4X((K1-1)(2M-1)(2N-1)+K2,

(K3-1)(2M-1)(2N-1)+K4)=

(5)

式中,C4w表示高斯色噪声对应四阶累积量矩阵,且在理想情况下,其恒等于零[12],即C4w=0。B为扩展的阵列流行矩阵,其表达式为

B=A∘A

(6)

利用高阶累积量的估计方法具有较多优点,但其运算量大,导致计算复杂度增高。下面将讨论如何降低算法复杂度。

3.2 分段部分去冗余

由Kronecker乘积的规律,L型阵列中的高阶方向矢量较复杂,且包含大量冗余项。本文利用分段思想提出分段部分去冗余(SEG_INC_RR, incomplete redundancy removal through segmenting)的方法,以部分去除其中的冗余项。该方法有效去除矩阵的部分冗余元素,改进算法复杂度,保证了虚拟扩展后ESPRIT算法中满足旋转不变性的两个子阵阵元数相同,同时由于累积量矩阵的阵列扩展作用,部分去除冗余后不会造成孔径损失,且能分辨出的目标数多于物理阵元数,同时提高估计精度。

假设收、发端在x、y轴方向上均有2个阵元,即M=N=2,则收、发阵列的方向矢量为ar(θr,φr)=[1,e-jπcos(φr)sin(θr),e-jπsin(φr)sin(θr)]T,at(θt,φt)=[1,e-jπcos(φt)sin(θt),e-jπsin(φt)sin(θt)]T,令u=e-jπcos(φr)sin(θr),p=e-jπsin(φr)sin(θr),m=e-jπcos(φt)sin(θt),n=e-jπsin(φt)sin(θt),联合方向矢量a(θr,φr,θt,φt)∈C9×1,即

a(θr,φr,θt,φt)=ar(θr,φr)⊗at(θt,φt)=

[1,m,n,u,um,un,p,pm,pn]T

(7)

则高阶方向矢量B的每一列b(θr,φr,θt,φt)=a(θr,φr,θt,φt)⊗a(θr,φr,θt,φt),b(θr,φr,θt,φt)∈C81×1,b内存在大量的重复项,仅有36个元素为有效项：

{1,m,n,u,um,un,p,pm,pn,m2,mn,um2,umn,pm2,pmn,

n2,un2,pn2,u2,u2m,u2n,up,upm,upn,u2m2,u2mn,upm2,

upmn,u2n2,upn2,p2,p2m,p2n,p2m2,p2mn,p2n2}

(8)

根据以上对M=N=2情况下的研究,类推到一般情况,即当发射端在x、y轴方向上均有M(M≥2)个阵元,接收端在x、y轴方向上均有N(N≥2)个阵元时,a(θr,φr,θt,φt)∈C(2M-1)(2N-1)×1,b(θr,φr,θt,φt)∈C((2M-1)(2N-1))2×1。上述特殊情况中(M=N=2),36个有效项是完全去冗余的结果,本文算法中为保证虚拟扩展后的阵列仍满足旋转不变性,仅做部分去冗余的SEG_INC_RR运算。

图2中bother由首个元素仅为1、ui或pi(i=1,…,N-1)的所有段组成,b1m由首个元素仅包含mi(i=1,…,M-1)的所有段组成,b1n由首个元素仅包含ni(i=1,…,M-1)的所有段组成。

bother、b1m、b1n又可表示如下：

(9)

(10)

(11)

由于bother、b1m、b1n中有效项所处位置的规律均不同,接下来对bother、b1m、b1n分别使用不同的方式提取有效项,具体实现方法如下：

图2 分段部分去冗余

bother、b1m、b1n对应有效项位置的索引向量分别记为Ioth、Im、In。通过下面方法获取Ioth：

Ioth=[];

Ioth=[Ioth,s(2M-1)2(2N-1)+1:s(2M-1)2(2N-1)+(2M-1)(2N-1)];

end

通过类似方式获取Im、In即可得总的有效项位置索引向量如下：

I=[Ioth,Im,In];

I=sort(I);

由上节知,理想情况时接收信号对应四阶累积量矩阵可写为R4X=(A⊗A)C4F(A⊗A)H,其中包含了大量冗余项。同对高阶方向矢量矩阵的部分去冗余操作一样,利用索引向量I对R4X的行和列分别作如下的部分去冗余操作：

((2M-1)(2N-1))2×((2M-1)(2N-1))2→(2N-1)2(M2+2M-2)×((2M-1)(2N-1))2

→ (2N-1)2(M2+2M-2)×(2N-1)2(M2+2M-2)

R4X(I,I)

(12)

其中,R4X(I,I)即是信号对应四阶累积量矩阵通过部分去冗余操作后所得的结果。

经过上述变换,矩阵R4X的大小从((2M-1)(2N-1))2×((2M-1)(2N-1))2降到(2N-1)2(M2+2M-1)×(2N-1)2(M2+2M-1),去除了R4X中大量的冗余项,极大地减小了矩阵维数,改进了算法的计算复杂度。

4 FOC-ESPRIT-MUSIC算法联合估计DOA、DOD

4.1 FOC-ESPRIT算法估计二维DOA

由前面章节的推导,通过3.1节四阶累积量的定义计算出第2节中接收信号模型对应四阶累积量矩阵R4X,并利用3.2节所提分段部分去冗余的方法去除R4X中的部分冗余项,得到含部分冗余项的四阶累积量矩阵R,最后对R进行特征值分解,取K个较大特征值对应的特征向量组成US。

根据(3)中A的结构,可将高阶方向矢量B=A∘A分块表示如下

(13)

(14)

由(14)式的对应关系,可得下式

(15)

(16)

(17)

(18)

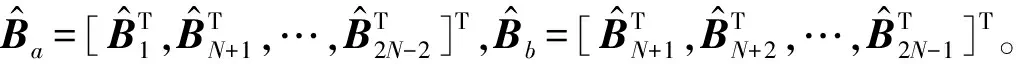
(19)

uk=-angle(λk)/π=cos(φrk)sin(θrk)

(20)

vk=-angle(rk)/π=sin(φrk)sin(θrk)

(21)

则第k个目标相对接收阵的二维角度,也即DOA仰角和DOA方位角的求解式依次为

(22)

(23)

仰角和方位角可自动配对。

4.2 FOC-MUSIC算法估计二维DOD

首先根据接收阵列的方向矩阵求解发射阵列的方向矩阵,再重构信号Z,同时构造信号Z的四阶累积量矩阵,使用FOC-MUSIC,将上节所得二维DOA估计值带入FOC-MUSIC谱函数,并通过二维谱峰搜索获得DOD方位角及DOD仰角[13]。寻找一个合适的行交换矩阵Q以保证下式成立,

(24)

其中Φtx=diag(exp(-jπcos(φt1)sin(θt1)),L,exp(-jπcos(φtK)sin(θtK))),Φty=diag(exp(-jπsin(φt1)sin(θt1)),L,exp(-jπsin(φtK)sin(θtK)))。

通过发射矩阵的方向矢量G重构信号Z,由式(2)得：

(25)

由前面推导算出重构信号Z对应含部分冗余项的四阶累积量矩阵R4Z,并特征值分解R4Z以求解出EN,EN是由后(2N-1)2(M2+2M-2)-K2个较小特征值对应的特征向量张成的噪声子空间[14],即EN=span[ek2+1,ek2+2,...,e(2N-1)2(M2+2M-2)]。EN与ES正交,可得本文对应的FOC-MUSIC谱函数为

(26)

5 仿真实验与分析

本文通过蒙特卡罗(Monte Carlo)实验来说明所提算法的估计性能。设仿真次数C_total=100,收、发端阵元间的间隔dr及dt均取半个波长,即dr=dt=λ/ 2,且阵元数M=N=4。假设K=3个非相关点目标的离开角和接收角分别为(φt1,θt1,φr1,θr1)=(30°20°5° 19°),(φt2,θt2,φr2,θr2)=(40° 40° 20° 30°),(φt3,θt3,φr3,θr3)=(60°70° 80° 60°)。快拍数Ls=200,一个周期码元数H_num=128,发射端采用相互正交的Hadamard码。

实验1在SNR=10 dB 条件下,FOC-ESPRIT-MUSIC算法散布图仿真结果如下：

图3 本文算法的接收角(DOA)估计散布图

图4 本文算法目标离开角(DOD)估计散布图

从图3、图4可以看出,在高斯色噪声背景下,本文算法能正确估计出目标的二维DOA、二维DOD角度信息。

实验2算法仿真性能分析。为说明所提算法性能,分别求解DOA和DOD的均方根误差(root mean square error, RMSE),仿真参数不变,定义

式中,αmk和βmk分别表示第k个目标的仰角和方位角在第m次实验中的仿真结果,α0k和β0k分别为对应的实际值。图5、图6分别体现了不同算法中DOA和DOD估计的RMSE随SNR的变化,同时描绘了本文算法用于白噪声背景条件下的估计性能曲线图。从图可知,本文算法在收发二维角度的估计性能上,SNR从1 dB开始逐渐增加过程中,角度估计的RMSE变化曲线趋于平稳,而且即使在较低信噪比条件下估计性能仍相对较好,除此之外,由于四阶累积量能有效地抑制高斯色噪声,本文的四阶累积量算法比基于二阶统计量的ESPRIT-MUSIC算法具有更高的估计精度,估计性能具有明显的优势,充分地表现了四阶累积量能最大限度地抑制高斯过程,即具有盲高斯性。从图中也可看出,本文算法适用于白噪声背景条件下的估计场景,且此时算法的整体估计性能较好。

图5 DOA估计均方根误差比较

图6 DOD估计均方根误差比较

图7 不同快拍下DOA估计性能

图8 不同快拍下DOD估计性能

6 结论

本文主要针对色噪声背景中在双基地MIMO雷达内使用L型阵列结构来联合估计目标的多维角度信息以及降低多维估计计算复杂度高的问题,提出了一种基于分段部分去冗余的FOC-ESPRIT-MUSIC算法。由于收发端均选用了L型阵列结构,可估计出目标的四维角度信息,更有利于目标定位。使用SEG_INC_RR方法去除累积量矩阵中的部分冗余项,极大程度地降低了算法复杂度,并且本文方法首先利用FOC-ESPRIT估计DOA二维角度,再利用FOC-MUSIC将DOA二维角度的估计值带入相应谱函数以估计DOD二维角度,提高了DOD估计精度,参数无需额外配对,且免除了高维谱峰搜索,进一步改善算法复杂度,同时四阶累积量的引入有效地抑制了空间色噪声的影响,由于其能虚拟阵列扩展阵列,增大了系统可识别目标的数量,能在工程上实现更好的应用。今后研究的关注方向将是如何实现完全去除L型阵列结构系统中四阶累积量的冗余项。

[1] Zhu W, Tang J. Robust Design of Transmit Waveform and Receive Filter For Colocated MIMO Radar[J]. IEEE Signal Processing Letters, 2015, 22(11):2112-2116.

[2] Tang Y, Lu Y. Single transceiver-based time division multiplexing multiple-input-multiple-output digital beamforming radar system: concepts and experiments[J]. Iet Radar Sonar & Navigation, 2014, 8(4):368-375.

[3] Zhang X, He Z, Rayman-Bacchus L, et al. MIMO Radar Transmit Beampattern Matching Design[J]. Signal Processing IEEE Transactions on, 2015, 63(8):2049-2056.

[4] Li M, Lu Y. Maximum likelihood DOA estimation in unknown colored noise fields[J]. IEEE Transactions on Aerospace & Electronic Systems, 2008, 44(3):1079-1090.

[5] 郑志东, 牛朝阳, 张剑云. 单快拍数下双基地MIMO雷达的角度估计[J]. 信号处理, 2010, 26(5):789-794.

Zheng Zhidong, Niu Zhaoyang, Zhang Jianyun. Receiver and Transmitter Angle Estimation for Bistatic MIMO Radar with Single Snapshot[J]. Signal Processing,2010, 26(5):789-794.(in Chinese)

[6] Liu J, Zhou W, Wang X. Fourth-order cumulants-based sparse representation approach for DOA estimation in MIMO radar with unknown mutual coupling[J]. Signal Processing, 2016, 128(C):123-130.

[7] 王彩云,龚珞珞,吴淑侠. 色噪声下双基地MIMO雷达DOD和DOA联合估计[J]. 系统工程与电子技术,2015, 37(10):2255-2259.

Wang Caiyun, Gong Luoluo, Wu Shuxia. Joint DOD and DOA estimation for bistatic NINO radar in the presence of colored noise[J]. Systems Engineering and Electronics, 2015, 37(10):2255-2259. (in Chinese)

[8] Jinli C, Hong G, Weimin S. Angle estimation using ESPRIT without pairing in MIMO radar[J]. Electronics Letters, 2008, 44(24):1422-1423.

[9] Zheng G, Chen B. Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar[J]. Multidimensional Systems and Signal Processing, 2015, 26(1):159-178.

[10]孙中伟,张小飞,吴海浪,等. L型阵列双基地MIMO雷达的传播算子多维角度估计[J]. 应用科学学报,2014,32(1):57- 64.

Sun Zhongwei, Zhang Xiaofei, Wu Hailang, et al. Multi-dimensional Angle Estimation in Bistatic MIMO Radar for L-Shaped Array with Propagator Method[J]. Electronics and Information Engineering,2014,32(1):57- 64. (in Chinese)

[11]孙中伟. 双基地MIMO雷达的目标定位[D].南京：南京航空航天大学,2012.

Sun Zhongwei. Target Localization in Bistatic MIMO Radar System[D]. Nanjing：Nanjing University of Aeronautics and Astronautics, 2012.(in Chinese)

[12]Wang Y, Trinkle M, Ng W H. Two-stage DOA Estimation of Independent and Coherent Signals in Spatially Coloured Noise[J]. Signal Processing, 2016, 128:350-359.

[13]Shi W, Huang J, He C, et al. Joint Direction-Of-Departure and Direction-Of-Arrival estimation in MIMO array[C]∥Tencon 2013-2013 IEEE Region 10 Conference. IEEE, 2013:1- 4.

[14]吴娜, 司伟建, 焦淑红,等. 基于去特征处理的信源数估计算法[J]. 系统工程与电子技术, 2015, 37(3):509-514.

Wu Na, Si Weijian, Jiao Shuhong, et al. New source number estimation method based on feature eliminated proess[J]. Systems Engineering and Electronics, 2015, 37(3):509-514. (in Chinese)