火车车轴悬臂弯曲试验机有限元分析

王晓东， 王丽， 张炜， 张明星

（长春工业大学 a.工程训练中心；b.机电工程学院，长春130012）

0 引言

火车车轴弯曲性能是保证火车安全行驶的重要条件，为了保证车轴的性能，需要通过弯曲试验对其进行分析，因此与之相对应的疲劳试验机则必不可少。疲劳试验机一般用于检测样件的力学性能和预测疲劳寿命，因此合理进行疲劳性能试验很有必要性。

从早期模拟车轴的弯曲疲劳试验机发展至今，已经有着上百年的历史。随着工业的发展，出现了多种疲劳试验机，比如模拟拉压、扭转等状态的试验机，广泛应用到交通、机械工程等各个领域[1]。但是随着科技发展对疲劳试验机的要求也越来越高，其本身是否能够更好地完成疲劳试验也是所需要重点考虑的问题之一。

本文为了更好地分析火车车轴的弯曲性能，对火车车轴悬臂弯曲试验机进行设计和分析，所设计的悬臂弯曲试验机符合GB/T2611-07《试验机通用技术要求》相关要求[2]。悬臂弯曲试验机是模拟火车在运行中车轴受力情况，现有试验机结构单一、成本较高，而且国内多数以研究试验机的某部分结构为主，对整体疲劳试验机的研究较少。因此本文针对这一问题对疲劳试验机进行设计[3]，为了保证所设计的试验机具有良好的工作性能，保证试验的顺利进行，还对其力学性能和疲劳寿命进行了有限元分析，根据结果判断该疲劳试验机是否符合试验需求。

1 车轴悬臂弯曲试验机的设计

车轴悬臂弯曲试验机根据车轴型号的不同结构也不尽相同，需按照国家标准进行设计。所设计的悬臂弯曲试验机车轴一端固定在旋转承载盘上，另一端与垂向加载机构相连，施加垂向载荷。垂向加载连杆与车轴通过轴承连接。旋转承载盘及其连接轴承应具有较大的承载能力，可抵抗5 kN·m的弯矩下的旋转疲劳作用。旋转承载盘由电动机驱动旋转，转速不低于1500 r/min，其车轴循环试验次数应不少于107次，车轴试样加载端应具有良好的抗摆动能力以保证加载的准确性。火车车轴悬臂弯曲试验机主要设计步骤如图1所示。

车轴悬臂弯曲试验机主要用于模拟火车实际运动时车轴受力情况，从而对车轴弯曲性能进行检测。由于车轴实际尺寸较大，故在保证不影响正常试验的情况下，现按照实际车轴的1/7进行试验机的设计。所设计的悬臂弯曲试验机主要包括轴向加载机构、旋转驱动机构、夹紧机构和主体框架等部分[4]。轴向加载机构用于模拟车厢对车轴所施加的压力，旋转机构用于模拟车轴实际运动过程中的旋转，夹紧机构主要针对车轴的轴端进行支撑和限位，主体框架用于支撑。利用CATIA建立车轴悬臂弯曲试验机的三维模型，其结构如图2所示。

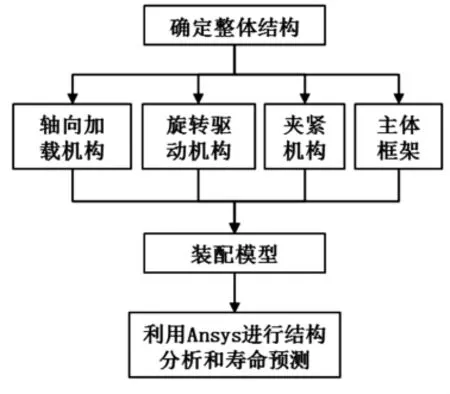
图1 试验机设计步骤

2 疲劳试验机有限元方法

疲劳试验机有限元分析的疲劳寿命计算方法主要包括名义应力法、局部应力-应变法和断裂学法。名义应力法计算全寿命，主要用于高周疲劳；局部应力-应变法用于计算裂纹的形成寿命；断裂学法用于计算裂纹扩展寿命。由于车轴悬臂弯曲疲劳试验机属于高周疲劳试验，因此采用名义应力法进行分析。应用名义应力法[5]分析的主要过程包括：根据结构及载荷进行有限元分析，分析危险部位应力情况；建立结构的S-N曲线；选择合适的疲劳累积损伤规则；进行疲劳分析，预测试验机寿命。

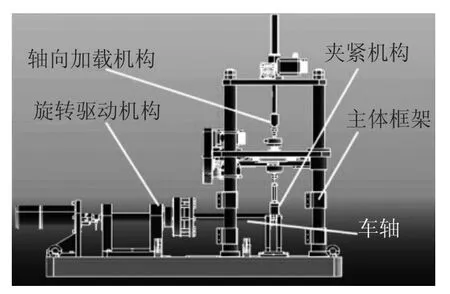
图2 火车车轴悬臂弯曲试验机

2.1 建立S-N曲线

根据典型的S-N曲线可知，一条完整的S-N曲线分为低周疲劳区（LCF）、高周疲劳区（HCF）和亚周疲劳区（SF），而本试验机属于高周疲劳，因此S-N曲线在对数系坐标上几乎为一条直线。采用幂函数绘制S-N曲线[6]，其表达式为

式中：α和C为材料常数；S为应力幅平均值。

将式（1）改为对数形式可得：

式中：a=lg C；b=-α，查表[7]可得a=46.4561，b=-15.6866,因此式（2）可写为

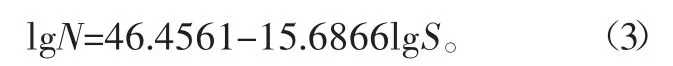
在ANSYS中所得线性S-N曲线如图3所示。

图3 所得S-N曲线

应力比不同时，其疲劳极限也不尽相同。通过试验测定不同应力比下的疲劳极限也比较困难，因此在分析时，可以选择经验模型进行估算。现有的经验模型主要包括Soderberg直线模型、Gerber抛物线模型、Goodman直线模型以及折线模型。

Gerber抛物线模型：

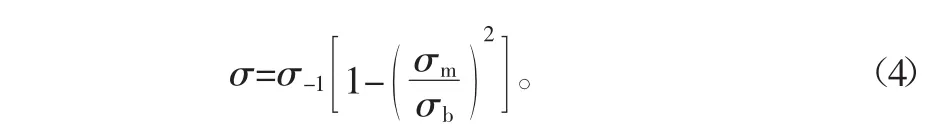
Goodman直线模型：

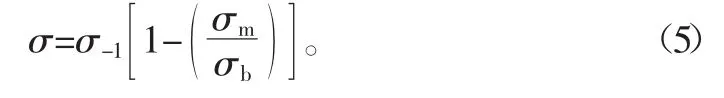
Soderberg直线模型：

折线模型：

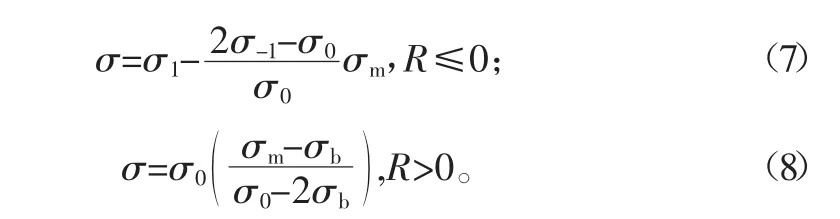
所述的模型疲劳极限图如图4所示。由图可以看出，Gerber抛物线模型可能偏于危险，而Soderberg直线模型相对较为保守，因此Goodman模型和折线模型比较合适，本文选择Goodman直线模型。

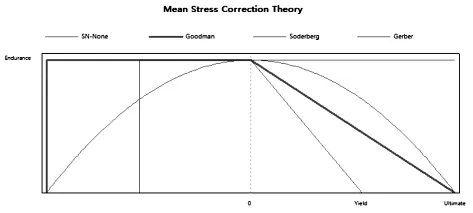
图4 模型疲劳极限图

2.2 疲劳累积损伤规则的选择

疲劳损伤理论研究的是在疲劳载荷作用下的疲劳损伤的累积规律，这在疲劳寿命的预测中有着重要意义。任何一个疲劳累积损伤理论必定以疲劳损伤D的定义为基石，以疲劳损伤的演化d D/d n为基础。根据疲劳损伤累积规律，主要分为线性疲劳累积损伤理论、修正的线性疲劳累积损伤理论和非线性疲劳累积损伤理论这3类[8]。

在工程应用中，虽然有多种损伤理论可供选择，但是线性疲劳累积损伤理论最为常用。由于线性疲劳累积损伤理论能够较好地预测疲劳寿命，而且能够更好地应用于高周疲劳，因此本文选择该理论进行疲劳寿命的分析。

线性累积损伤理论中最为典型的为Palmgren-Miner理论，简称Miner理论[9]，该理论为：

一个循环造成的损伤：

等幅载荷下n个循环造成的损伤：

变幅载荷下n个循环造成的损伤：

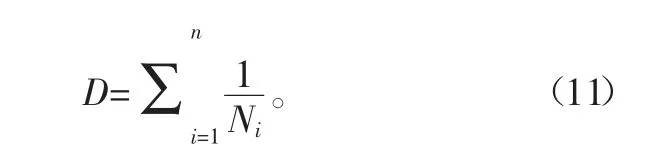
临界疲劳损伤：若为常幅循环载荷，即n=N，由式（11）可得

3 有限元模型的建立

现利用ANSYS Workbench分析软件[10]对所设计的车轴悬臂弯曲试验机进行仿真[11]，并分析其受力变化情况。其分析流程主要步骤如图5所示。

3.1 有限元模型的简化

由于所设计的模型应尽可能地与实际情况接近，因此模型在设计上应较为精细，但是这在仿真过程中将会增加工作量，对硬件也要求较高，因此，为了方便仿真分析，节省计算时间，可以针对模型进行简化处理，将外壳、不必要的支撑结构、装配工艺孔等进行忽略，过滤圆角等细节。简化后的模型如图6所示。

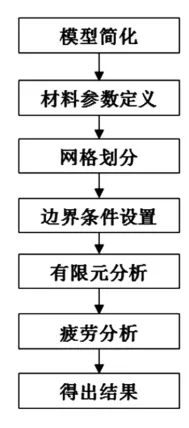
图5 有限元分析步骤

3.2 材料参数的设定

进入ANSYS材料库进行材料的设置，针对不同零部件的情况，在“Engineering Data Sources”中分别对零件进行模型的材料定义。添加所需要用到的材料，对材料进行命名，设置材料的属性并保存，进入DM界面，对零部件进行材料的选择。

3.3 有限元网格的划分

图6 简化后的模型

网格划分是否合理将直接影响进一步分析，因此网格划分是有限元分析的重要步骤[12]。进入ANSYS的Model操作环境中去，根据模型的尺寸，利用sizing选项对模型进行网格划分。选定连续划分的模型结构，根据模型大小，设定划分的单元尺寸大小，选择Generate按钮，生成模型的网格。所划分后的网格模型如图7所示。

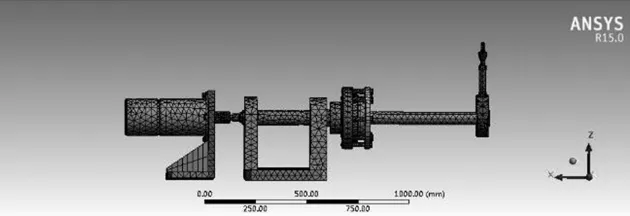
图7 试验机网格模型

根据整体机构的各零部件的性能以及装配方式，需要对接触[13]方式进行定义。所涉及到的接触主要分为6种类型。车轴悬臂弯曲试验机的零部件连接主要包括轴承连接、螺栓连接、键连接等，分别针对不同连接方式进行不同的接触定义。螺栓与零件和轴承与轴之间的连接部分均属于没有相对运动的固定连接，因此选择绑定接触；轴承内部属于有摩擦的接触，由于属于滑动摩擦，因此选择滑动摩擦接触类型。在存在相互运动的部件之间先选择“Frictionless-无摩擦”接触命令，存在利用螺栓连接的紧固件选择“Bonded-绑定”接触命令。

3.4 边界条件设置

在DM环境中，对模型施加转矩和约束力。车轴悬臂弯曲试验机的车轴转速为1500 r/min，在车轴的轴向加载机构上施加加载力，试验加载力为F=7 kN，对底座部分添加固定约束。在“Displacement”中设置X、Y、Z三个轴方向的位移量为0。在分析界面添加“Total Deformation”与“Equivalent Stress”设置，并添加疲劳分析工具。

4 试验结果的分析

添加应力和应变选项，进行仿真分析，所得到的应力和应变云图如图8、图9所示。

图8 试验机应力分布云图

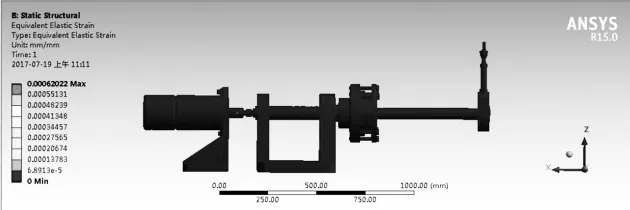
图9 试验机应变分布云图

通过分析结果可知，在载荷力的作用下，最大载荷力发生在轴与旋转承载盘连接的位置，其最大应力为107.25 MPa，最大应变为0.0006 mm，属于微小的应变。通过查表可知45钢的疲劳极限强度σ-1=388 MPa，则根据强度校核[14]公式：其中:有效应力集中系数Kσ=1.73；尺寸系数ε=0.83;表面质量系数β=0.99，代入式（13）可得：

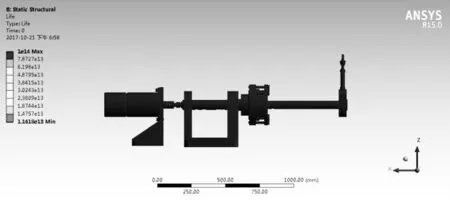
图10 疲劳寿命云图

图11 最小寿命值

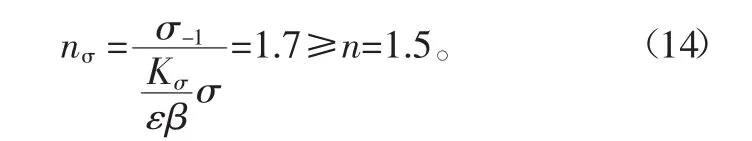
因此可知，所设计的试验机能够满足实验条件所承受的加载力，使得试验机能够稳定地运行。

根据名义应力法进行疲劳分析[15]，选择Goodman模型和线性累积损伤理论进行疲劳寿命的计算，所得到的疲劳寿命云图如图10所示，其寿命最小值如图11所示，为1.1618×1013次循环，符合不少于107次循环的设计需求。

5 结论

根据试验机的设计标准建立火车车轴悬臂弯曲试验机模型，并对试验机进行有限元分析。主要建立了车轴悬臂弯曲试验机的模型，选择合适的有限元方法和疲劳累积损伤规则，介绍了材料的S-N曲线和有限元分析的基本步骤，实现对火车车轴悬臂弯曲试验机的分析。通过分析所得到的应力及应变分布云图可知，所设计的试验机结构性能良好，通过疲劳寿命云图可知该试验机能够达到试验要求的循环次数，从而可知所设计的试验机满足火车车轴悬臂的试验要求。