复杂岩性储层横波速度预测研究——以四川盆地A油田为例

2018-08-18刘致秀折向毅

石油地质与工程 2018年4期

刘致秀，折向毅

刘致秀1，折向毅2

（1．庆阳职业技术学院，甘肃庆阳 745000；2．西北有色勘测工程公司）

测井横波速度是进行地震资料反演的重要原始资料，但很多老井区缺乏横波测井资料。针对此问题，以A油田侏罗系珍珠冲段复杂岩性储层为研究对象，进行两方面研究：①将储层等效为具有一定形状的多种矿物颗粒、孔隙及其中流体的混合物，基于自适应（SCA）岩石物理模型，联合Gassmann方程、Wood方程建立速度预测流程；②针对包含两种岩性（砂岩和泥岩）岩石的Xu–White岩石物理模型扩展为针对包含多种矿物岩石的岩石物理模型（称为多矿物扩展Xu–White岩石物理模型）。A油田侏罗系实际数据中的应用表明，多矿物扩展Xu–White模型的速度预测结果优于Xu–White模型；基于自适应模型的速度预测结果优于多矿物扩展Xu–White模型。

自适应（SCA）岩石物理模型；Gassmann方程；Xu–White岩石物理模型；速度预测

横波测井速度是叠前地震资料反演所必须的原始资料，主要作用是进行地震合成记录以提取子波，建立低频模型及反演中作为约束。没有准确的测井横波资料就很难进行准确的叠前资料反演。在实际生产中，由于成本及技术条件限制，往往缺乏测井横波速度信息，尤其是在老井中。在这种情况下，使用一定的方法，通过常规测井资料对横波速度进行预测就成为叠前反演的关键。在这方面，主要方法有经验公式法和岩石物理模型法。经验公式法是根据研究目标区的岩心测量数据或者测井数据，回归总结速度与孔隙度、泥质含量之间的关系或者总结横波速度与纵波速度之间的关系，使用这些关系式进行速度预测[1–6]。

1 基于自适应（SCA）岩石物理模型的速度预测方法

2 多矿物改进的Xu–White岩石物理模型

Xu–White（1995）综合Wyllie方程、Kuster–Toköz模型、微分等效介质模型（DEM）、Gassmann方程以及Wood方程，提出了针对砂泥岩的岩石物理模型。该模型将矿物分为砂岩、泥岩两部分，将孔隙分为大孔隙纵横比的砂岩孔隙（约0.12）和小孔隙纵横比的泥岩孔隙（0.02~0.05）两部分。该模型兼具Kuster–Toksöz模型描述复杂孔隙形状和Gassmann方程考虑孔隙流体影响的优点，得到了较好的效果。

图1 Xu-White模型及多矿物扩展Xu-White模型建模流程

然而，岩石中的矿物是非常复杂的，即便所谓的纯净的砂岩，其中往往也还有其他矿物，比如黏土或者钙质矿物，等效为简单的矿物往往会影响速度预测的效果，矿物的分析精度直接影响着岩石基质弹性模量的准确程度，矿物分析的越精确，计算的基质弹性模量越准确；对应的，速度预测的精度也较高[7]。本文将砂岩（石英），灰岩（方解石），白云岩（白云石）四种矿物含量引入Xu-White模型，对原始Xu-White模型的砂、泥两相修正后，Xu-White模型能够应用于多种矿物的情况。

3 实例研究

以四川盆地A油田侏罗系珍珠冲段某井复杂岩性为例进行速度预测研究。该段发育复杂岩性储层，矿物主要包括石英、黏土、方解石、白云石，储层段孔隙度为8%~3%。

使用复杂岩性处理程序（CRA）多矿物测井解释方法(雍世和)求取黏土、石英，方解石，白云石四种矿物体积含量以及孔隙度、饱和度，将这些数据引入新构建的岩石物理模型进行速度预测。使用经过矿物扩展的Xu–White岩石物理模型作为对比例。所谓矿物扩展的Xu–White岩石物理模型，是指将原本针对以砂泥岩（包括石英、黏土两种矿物）的Xu–White模型扩展为能够考虑四种矿物（石英、黏土、方解石、白云石）。延续原始Xu–White岩石物理模型中考虑孔隙类型的思路，将石英、方解石、白云石等刚性颗粒中的孔隙纵横比设定为0.12，其在总孔隙度中的占比与三种矿物在岩石总矿物含量中的占比一致；令黏土裂缝的孔隙纵横比为0.02，其在孔隙度中的占比与黏土在岩石总矿物含量中的占比一致[8–11]，计算中使用的主要参数如表1。

表1 主要矿物及流体弹性参数

图2为多矿物扩展的Xu-White岩石物理模型速度预测结果与本文提出的新方法所得结果的对比。图中红色曲线为原始数据，浅蓝色曲线（preXW3, DSpreXW3）为多矿物修正模型的结果，黑色曲线(pre–,pre–）为新方法预测的结果。由图可见，两种方法所得纵波时差（）的精度都较高，与实测数据基本接近；而本文方法所得横波速度预测结果的精度明显高于多矿物扩展的Xu–White模型的结果，尤其在690~720 m，本文方法所得结果与实测数据更加接近，说明在孔隙发育的层段，本文方法更适用。

计算预测速度与实测速度之间的相对误差（预测时差-实测时差)/实测时差），如图3所示，两种方法所得的纵波时差误差小于横波时差误差；基于SCA理论所预测的纵波和横波误差都明显小于岩性扩展的Xu–White模型所得结果。这证明了在研究区的复杂岩性储层中，新的模型所预测的结果优于矿物扩展的Xu–White模型所预测的结果。

4 结论

（1）将储层岩石等效为具有一定形状的多种矿物颗粒及孔隙相的混合物，结合自适应岩石物理模型、Gassmann方程、Wood方程以建立岩石物理模型，该岩石物理模型速度预测结果优于多矿物扩展Xu–White模型及原始Xu–White模型。

（2）使用多矿物扩展Xu–White模型比砂泥两相矿物模型所得速度预测结果更为精确，证明矿物基质越精确，所建立岩石物理模型越精确。

图2 多矿物扩展Xu–White岩石物理模型与基于SCA的模型速度预测结果对比

注：preXW3——修正的Xu-White模型速度预测纵波时差，preXW3——横波时差，pre–——基于新方法预测的纵波时差，pre–——横波时差；其中红色曲线为实测曲线(，)，蓝色及黑色为预测曲线

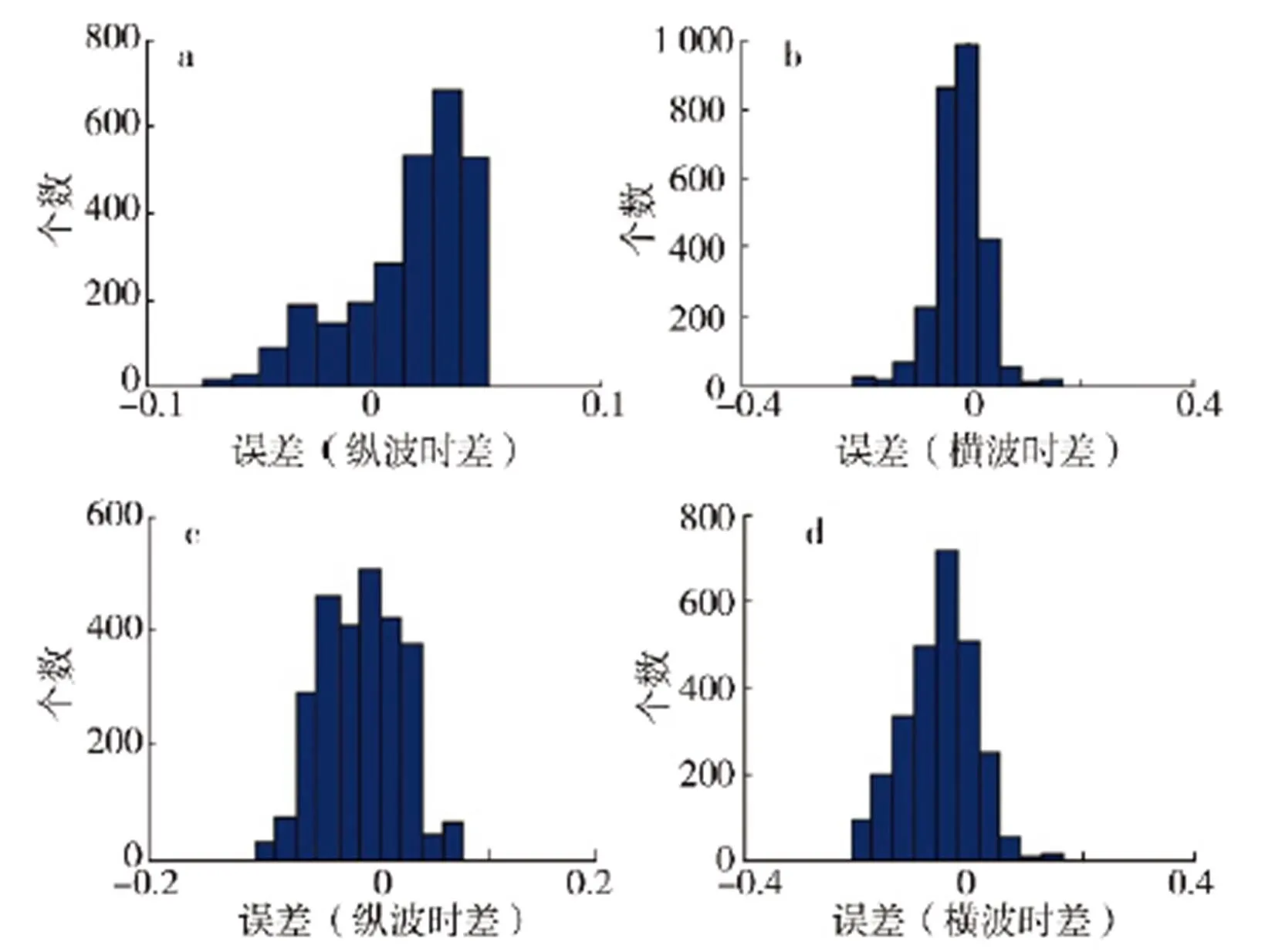
a和b为基于SCA模型的预测速度误差，c和d为修正Xu–White模型的预测速度误差

[1] WOOD A W. A textbook of sound[M]．New York：The MacMillan Co，1955，360．

[2] BIOT M A．Theory of propagation of elastic waves in a fluid saturated porous solid[J]．The Journal of the Acoustical Society of America，1956，28：168–191．

[3] WU T T．The effect of inclusion shape on the elastic moduli of a two–phase material [J]．International Journal of Solids Structures，1966，2：1–8．

[4] Berryman J G．Mixture theories for rock properties，in A handbook of Physical Constants[M]．America Geophysical Union，1995：205–228．

[5] XU S，White R E．A new velocity model for clay–sand mixtures[J]．Geophysical Prospecting，1995，43：91–118．

[6] 邵才瑞，印兴耀，张福明，等．利用常规测井资料基于岩石物理和多矿物分析反演横波速度[J]．地球科学（中国地质大学学报），2009，34（4）：699–707．

[7] 张广智，李呈呈，印兴耀，等．基于修正Xu–White模型的碳酸盐岩横波速度估算方法[J]．石油地球物理勘探，2012，47（5）：717–722．

[8] 郭栋，印兴耀，吴国忱．横波速度计算方法与应用[J]．石油地球物理勘探，2007，42（5）：535–538．

[9] 冯昕鹏，李金付，聂建委．横波速度拟合技术在苏里格气田的应用[J]．岩性油气藏，2012，24（6）：106–109．

[10] 谢月芳，张纪．岩石物理模型在横波速度估算中的应用[J]．石油物探，2012，51（1）：65–70．

[11] 张杨．利用Xu–White模型估算地震波速度[J]．成都理工大学学报（自然科学版），2005，32（2）：188–193．

编辑：赵川喜

2017-06-05

刘致秀，硕士，讲师，1984年生，2014年毕业于西安石油大学矿床学、矿物学、岩石学专业，现从事矿床学、矿物学、岩石学教学工作。