一种针对大规模社交网络的用户信任度预测算法

2018-08-17,

计算机工程 2018年8期

(江西财经大学软件与物联网工程学院,南昌 330013)

0 概述

随着计算机网络的快速发展,网络社交已经成为人们进行交流的主要方式之一[1]。近年来,社交网络中的用户量越来越庞大,网络结构也越来越复杂。如何快速准确地预测大规模社交网络中的用户信任度显得尤为重要。

通常情况下,信任是人们进行一切社交活动的基础[2]。同时,在实际中,信任被认为是社交网络中的一种特殊信息,其具有可传播性、弱传递性和不确定性等性质[3]。这些性质为研究预测社交网络中2个用户间的信任度提供了思路。例如:社交网络中的用户A与用户B素不相识,而在某个特定的环境下,A想要知道B是否可以信任。虽然A与B之前没有任何联系,但此时A可以通过咨询他的朋友来搜集关于B的信任信息,并结合相关的信任推理方法最后对B做出信任度预测。

目前,社交网络信任预测和个性化评估已被广泛研究[4],且被应用于多种领域,如网络安全、社交服务推荐[5]、P2P网络[6]、电子商务[7-8]、云计算[9]等。这些研究的主要思路为:首先,从社交网络中提取出相应的信任路径(信任图);然后,在该信任路径上采用一些典型的信任整合策略计算出用户的预测信任值,其中,基于图简化的信任度预测模型是研究较多的方式之一,较为典型的有Tidal Trust[10]、Mole Trust[11]和GFTrust[12]等算法。但是,这些算法通常只适用于小规模网络或在大规模网络中效率低下,且要求该网络中每条边都具有完整的信任关系。为解决这一问题,文献[13]建立一种基于“小世界”网络理论的信任图生成框架SWTrust。该框架主要根据用户活动域信息来计算用户的信任相关度,并结合弱连接理论和社会距离来从大规模社交网络中提取出一个信任图,然后在该信任图的基础上利用8种基于可靠性模型的信任整合策略计算出用户的预测信任值。但是,该方法所计算的用户信任度依赖信任的发起者和被评价的信任者(如source和target),导致其计算效率存在局限性。

针对以上方法的不足,本文提出一种针对大规模社交网络的用户信任度预测算法TTDTrust。综合考虑网络中节点的拓扑特征和用户信任率信息,并设计一种用户拓扑信任度指标来衡量用户信任信息。此外,该算法所计算的用户拓扑信任度独立于被评价的用户对,即计算网络中用户拓扑信任度的过程可在线下进行。最后,本文在真实的社交网络分析数据集上进行多次实验来验证该算法的有效性。

1 算法设计

1.1 相关定义

定义1(信任) 信任在不同领域有不同定义。本文主要采用文献[10]对信任的定义,即信任为“一个用户的行为将带来好的结果”。此外,信任分为推荐信任和功能信任[4]。推荐信任是指一个用户为某个用户推荐另一个用户的信任值,功能信任是一个用户对另一个用户的直接信任值。

通常情况下,2个用户间的信任有2种表示方式:1)二进制表示,即“1”表示信任,“0”表示不信任;2)将信任表示为[0,1]内的某一个数值[14],数值越大表示越信任。本文采用后者作为信任表示方法。

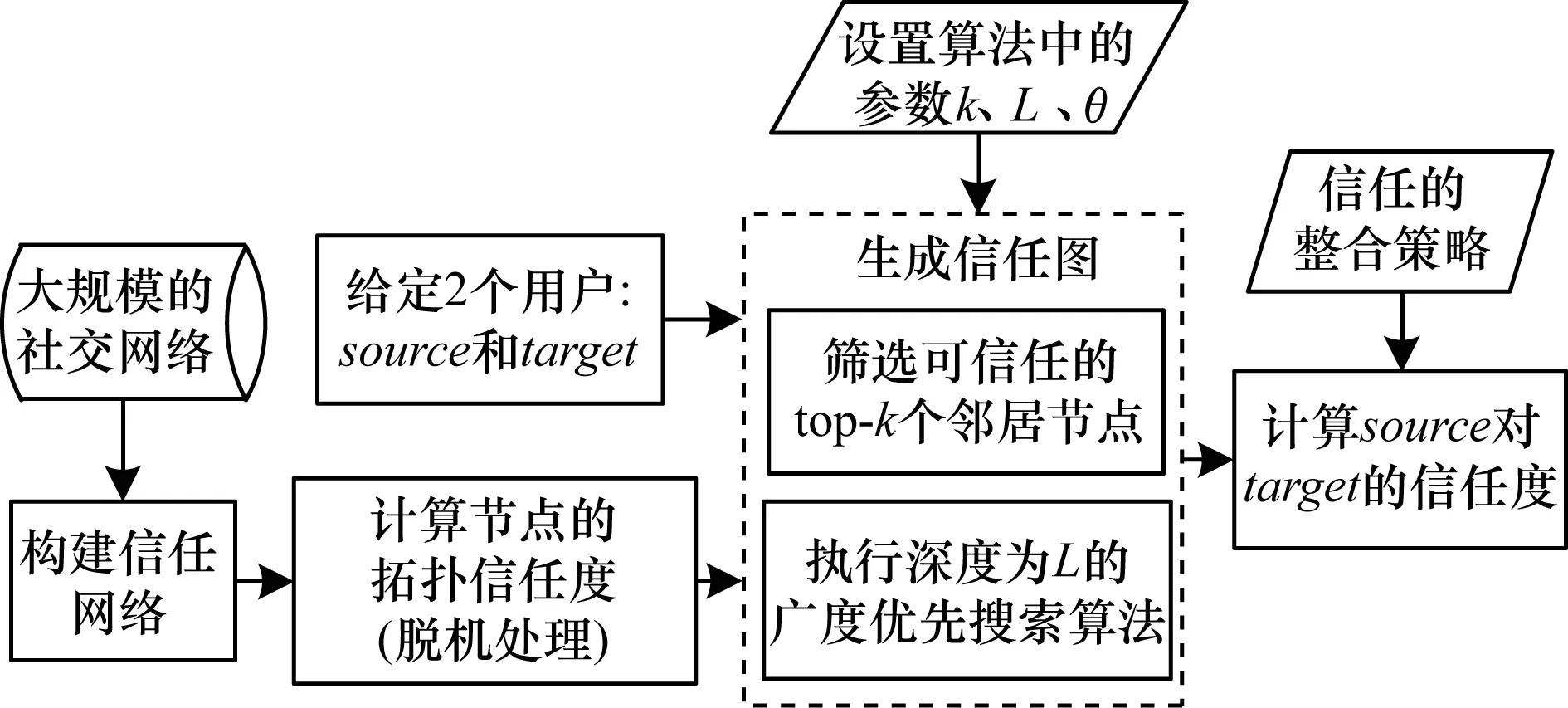
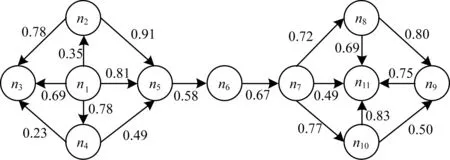
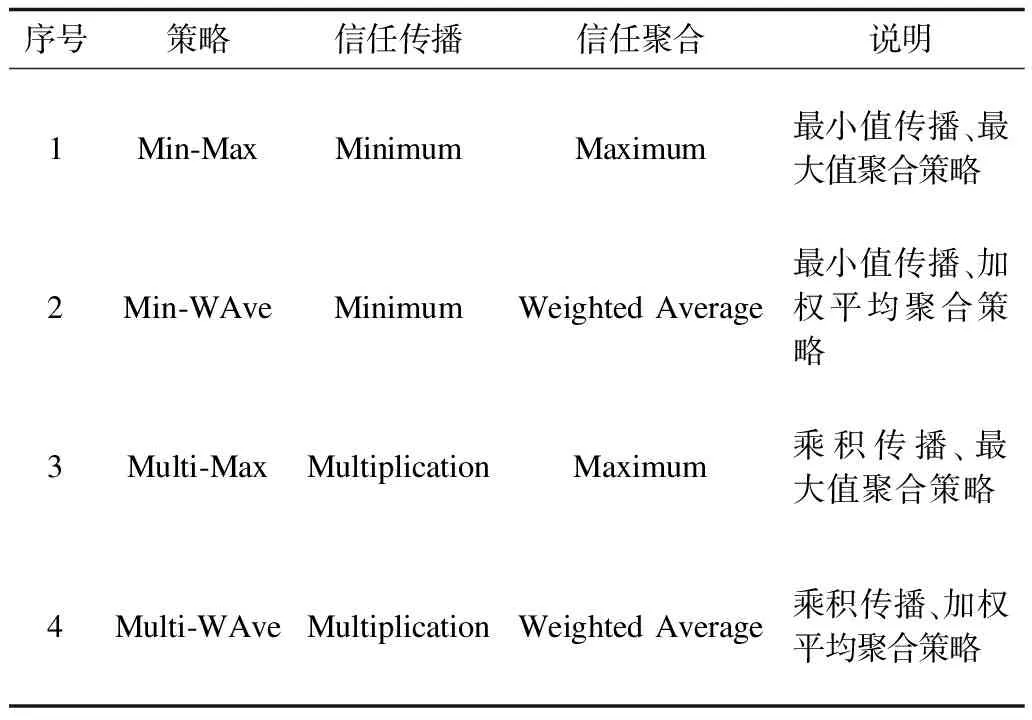
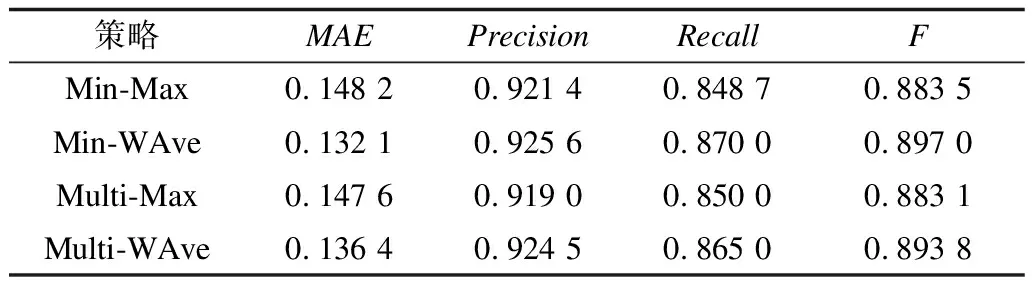
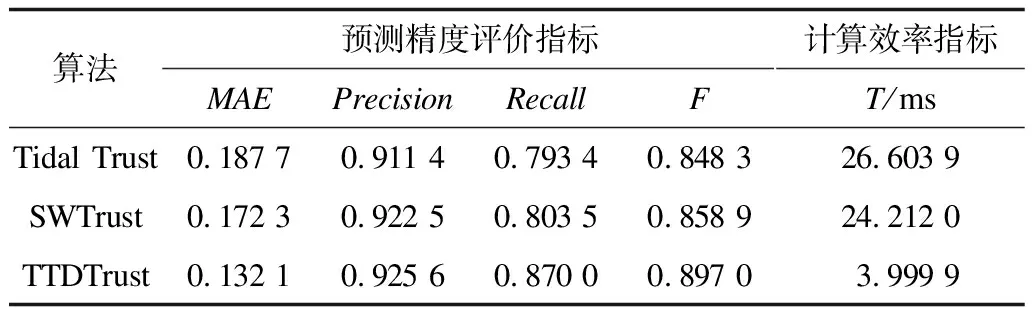
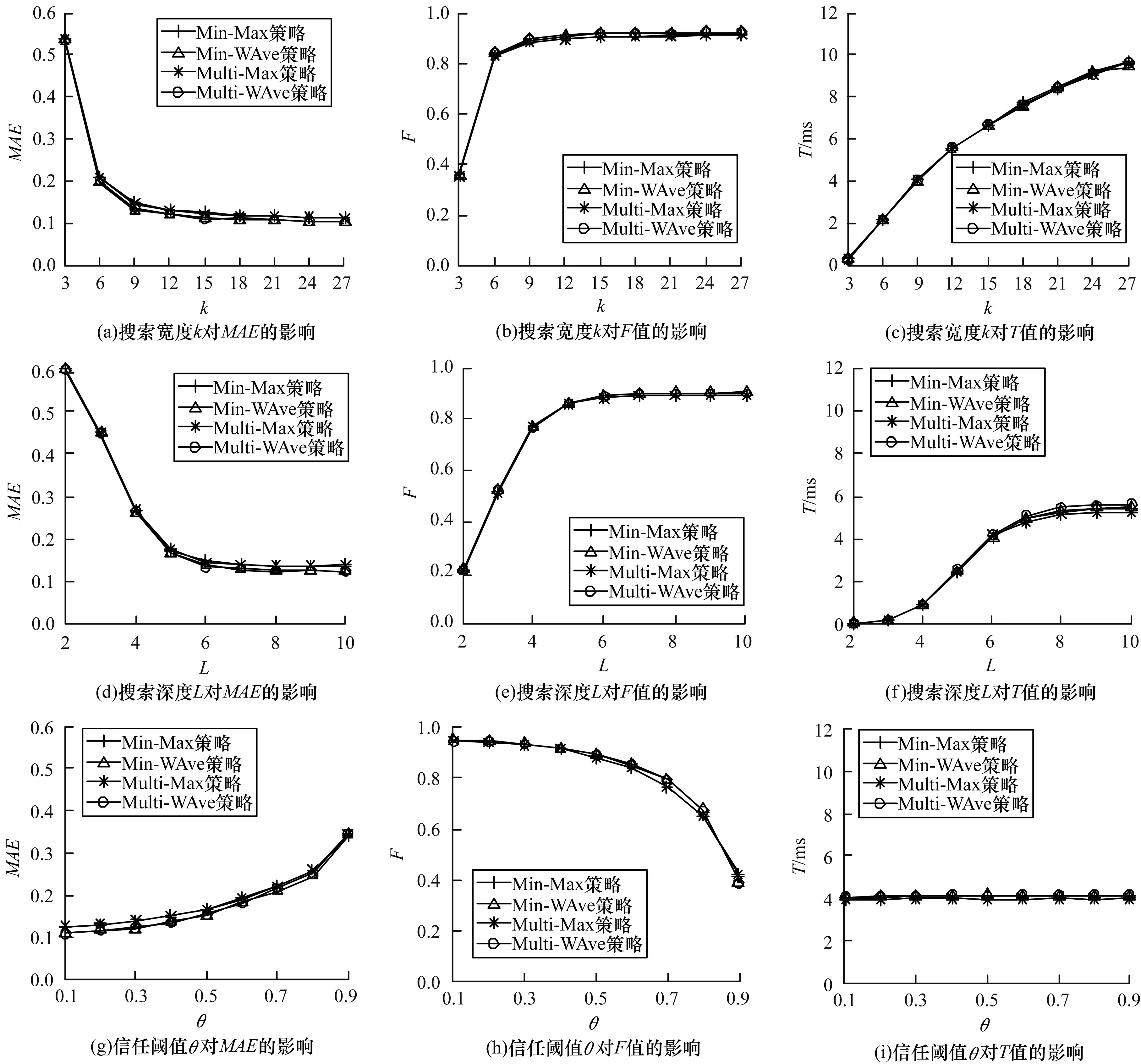
定义2(信任网络) 对于一个给定的社交网络,将其建模表示为对应的信任网络G=(N,E,W)。其中,N代表社交网络中的所有用户,E代表信任网络中的有向边集合,每一条有向边e(ni,nj)表示用户ni(ni∈N,0

定义3(信任路径) 对于给定的信任网络G=(N,E,W),如果该网络中的一个源节点source到另一个目标节点target之间存在一条可达的路径p=(source,…,ni,nj,…,target),且p中任意边e(ni,nj)上的权值tij大于信任阈值θ,则定义该路径p为信任路径。

定义4(信任图) 对于给定的信任网络G=(N,E,W),信任图由source到target间的所有信任路径构成。

1.2 算法框架

基于第1.1节的定义,本节进一步描述如何预测网络中源节点source对目标节点target的信任度。本文TTDTrust算法整体框架如图1所示。该算法旨在预测大规模社交网络中没有直接社交的2个用户之间的信任度,算法输入为原始大规模社交网络与2个待预测的用户source和target。

图1 TTDTrust算法整体框架

TTDTrust算法步骤为:1)将大规模社交网络建模表示为信任网络;2)计算信任网络中节点的拓扑信任度(在线下进行计算);3)根据节点的拓扑信任度筛选该节点可信任的top-k个邻居;4)执行深度为L的广度优先搜索算法,生成source到target的信任图;5)在该信任图上采用信任整合策略计算source对target的信任度。

1.3 拓扑信任度

在社交网络分析中,通常利用节点度[15]、紧密度[16]和介数中心性[17]等度量来评估节点的信息传播能力。其中,节点度因设计简单而被广泛运用,但其难以充分度量节点的信息传播能力。相比之下,紧密度和介数中心性因考虑到节点与节点之间的信息,可以较好地体现节点的信息传播能力,但是其计算复杂度较高。因此,这3种度量方法均难以直接应用于社交网络信任度预测中。文献[18]通过考虑节点邻居度信息,提出用一种局部中心性指标来评估节点的信息传播能力。通常,在该指标考虑节点三步内邻居的入出度情况时,就可以达到较好的效果,且其计算过程只需在一步节点度的基础上进行即可。因此,该指标不仅具有较好的信息传播能力,而且具备节点度计算简单的特点。基于此,本文提出一种新的度量节点信任能力的指标:拓扑信任度,该指标综合考虑网络节点的拓扑特征和用户的信任率信息。节点拓扑信任度如图2所示。

图2 节点拓扑信任度示意图

定义5(节点拓扑信任度) 图2中的一个信任网络G=(N,E,W)共有11个节点,边上权值为2个用户的信任率,则定义节点n1的拓扑信任度Tdegree(n1)的计算公式如下:

综上,对于一个给定的信任网络G=(N,E,W)和2个用户source、target,通过式(1)可以事先(脱机处理)计算出所有节点的拓扑信任度。

1.4 信任整合策略

通常情况下,信任整合包括2个步骤:

步骤1针对信任图中的每条路径整合出一个信任值。

步骤2聚合多条路径的信任值,即将步骤1中的所有信任值聚合成一个整体的信任度。

本文在实验过程中实现了基于可靠性模型[19]的4种信任整合策略,具体信息如表1所示。

表1 信任整合策略信息

1.5 TTDTrust算法描述

TTDTrust算法主要针对一个给定的大规模社交网络和用户source、target,预测source对target的信任度。其伪代码如算法1所示。

算法1TTDTrust

输入信任网络G,源节点source,目标节点target,搜索广度上界k,搜索深度上界L,信任阈值θ

输出source对target的信任度t(source,target)

1.Queue={source},tempQ={}//初始化队列Queue为

//source,tempQ为空

2.depth=0//初始化搜索深度为0

3.Spath={}//初始化信任路径集为空

4.while (Queue非空,且depth小于等于L)do

5.从Queue中取出最前面的元素,并赋给v节点

6.从v所有邻居中筛选出拓扑信任度最高的前top-k个邻居

7.for (v节点的top-k邻居中每一个节点u)do

8.查询获取u的拓扑信任度Tdegree(u)//事先通过式(1)

//线下计算并存储Tdegree(u)

9.if(u未访问,且Tdegree(u)大于θ)then

10.if(u是target节点)then

11.从target回溯source得到一条信任路径p

12.将p加入到Spath中

13.else

14.将u加入到tempQ中

15.标记u已经被访问

16.end if

17.end if

18.end for

19.if (Queue为空)then

20.将tempQ中的元素赋给Queue

21.depth增加1

22.清空tempQ

23.end if

24.end while

25.在Spath上分别利用4种信任整合策略计算出t(source,target)

26.return t(source,target)

TTDTrust算法具体流程如下:

步骤1初始化数据结构与参数(第1行～第3行)。队列Queue和tempQ分别用于存储当前层访问的节点和下一层访问的节点,depth用于记录每次遍历的深度,Spath={}用于存储最强信任路径集。

步骤2执行具有限制条件的广度优先搜索算法(第4行～第24行):1)只要队列Queue不为空,且搜索深度depth≤L,就取出Queue中最前面的节点并赋给节点v;2)根据之前线下计算存储的节点拓扑信任度,从v的所有邻居中筛选出拓扑信任度最高的前top-k个邻居;3)遍历该top-k个邻居中的每个节点u,查询u的拓扑信任度Tdegree(u);4)对u进行判断,如果u没有被访问且Tdegree(u)大于给定的信任阈值θ,则继续判断u是否为目标节点target,如果是目标节点,即从target回溯到source生成一条信任路径p,并把p添加到信任路径集Spath中,否则,标记u已经被访问,同时将u放入tempQ队列中;5)如果Queue为空,则将tempQ队列中的元素全部赋给Queue队列,同时将搜索深度depth加1,并清空tempQ队列。

步骤3分别采用表1中的4种信任整合策略计算出source对target的预测信任度t(source,target)(第25行)。

1.6 算法复杂度分析

TTDTrust算法的计算时间主要包括线下计算时间和线上计算时间2个部分。

1)线下计算时间。线下计算过程主要为计算网络中所有用户的拓扑信任度。该过程遍历每个用户三步邻居的边,即需要扫描3|E|条边,因此,该过程时间复杂度为O(|E|)。

综上,TTDTrust算法的总时间复杂度为O(|E|+|n|·logak),线上计算的时间复杂度为O(|N|·logak),远小于传统的全遍历信任度预测算法的复杂度O(|V|·|E|),尤其是在大型网络中,TTDTrust算法的时间复杂度优势更明显。

2 实验结果与分析

2.1 数据集说明与实验设置

本文采用真实的社交网络数据集Epinions[20]进行实验,实验中舍弃不存在信任关系的用户和边,最后得到7 375个用户节点和111 781条边。考虑到数据集中的信任表示为二进制类型,在实验过程中,本文采用文献[14]方法,将用户二值信任关系转换为[0,1]范围内的信任表示。具体方法为:首先,为每个用户节点赋一个质量qi∈[0,1],且qi～N(μ,σ2);然后,从[max(qj-δij,0),min(qj+δij,1)]范围内均匀地选取用户ni对nj的信任值t(ni,nj)。其中,δij=(1-qi)/2表示噪音系数,t(ni,nj)的范围为[0,1],其值越大表示ni对nj越信任。

本次实验使用的个人计算机配置为64位win7操作系统,处理器为Intel(R) Core(TM) i5-2400 CPU@3.10 GHz RAM 8 G。实验参数如表2所示。

表2 实验参数设置

实验过程采用留一法进行测试。实验次数τ=10 000,每次实验随机地抽取一条边进行测试,将第i次实验中2个用户之间的实际信任度值记为treal(i),预测信任度值记为tpred(i)。相应的信任度评估指标为平均绝对误差(MAE)、准确度(Precision)、召回率(Recall)和F值。各值计算公式为:

Precision=|SA∩SB|/SB

(3)

Recall=|SA∩SB|/SA

(4)

F=2×Precision×Recall/(Precision+Recall)

(5)

其中,SA、SB分别为实验随机抽取的边中treal(i)大于θ和tpred(i)大于θ的边集合。

2.2 算法性能分析

2.2.1 TTDTrust算法精度

为验证TTDTust算法的有效性,分别运用4种典型信任整合策略测试TTDTust算法的信任预测精度,实验结果如表3所示。

表3 TTDTrust算法的信任预测精度

由表3可以看出,在4种信任整合策略中,Min-WAve的MAE、Precision、Recall和F值都优于其他3种策略,即Min-WAve预测效果最好。此外,从表3还可以看出,4种策略的综合指标F最小值为0.883 1,最大值为0.897 0,该结果验证了TTDTust算法具有较高的信任预测精度。

2.2.2 TTDTrust算法与典型预测算法的对比分析

在社交网络信任度预测研究领域中,Tidal Trust算法[10]较典型,且其具有很强的代表性。此外,文献[13]提出的SWTrust算法也是针对大规模社交网络进行用户信任度预测研究,且是近几年社交网络信任度预测模型中效果较好的算法之一。因此,本节实验通过Min-WAve策略,进行TTDTrust算法与Tidal Trust算法、SWTrust算法的性能对比分析,实验结果如表4所示。其中,T表示算法运行时间。

表4 3种算法在Min-WAve策略下的性能对比分析

由表4可以看出,与Tidal Trust、SWTrust算法相比,TTDTrust算法MAE值分别降低了29.62%和23.33%,Precision值分别提高了1.55%和0.33%,Recall值分别提高了9.65%和8.27%,F值分别提高了5.74%和4.43%。此外,在计算效率上,因为TTDTrust算法的线上计算时间较少,所以其总体计算时间大幅减少,Tidal Trust算法的计算时间是TTDTrust算法的6.65倍,SWTrust算法的计算时间是TTDTrust算法的6.05倍。这些结果均能说明TTDTrust算法针对大规模社交网络用户信任度预测时具有较好的效率。

2.2.3 参数k、L、θ对TTDTrust算法的影响

TTDTrust算法涉及3个关键参数:k,L,θ。因此,本节实验分别测试参数k、L、θ对TTDTrust算法的影响,算法MAE值、F值、T值3个指标的实验结果如图3所示。其中,图3(a)～图3(c)的实验参数为k∈[3,27]、L=6、θ=0.5;图3(d)～图3(f)的实验参数为k=9、L∈[2,10]、θ=0.5;图3(g)～图3(i)的实验参数为k=9、L=6、θ∈[0.1,0.9]。

图3 参数k、L、θ对TTDTrust算法的影响

由图3(a)～图3(f)可以看出,在k∈[3,9]、L∈[2,6]范围内,随着k、L的增大,TTDTrust算法的MAE值逐渐减小,F值、T值均逐渐增加。随后,MAE值和F值开始收敛,T值增长放缓。此外,在图3(c)中,T值增长曲线的趋势与log函数基本相同。该结果与前文分析的TTDTrust算法时间复杂度为O(|N|·logak)相吻合。

由图3(g)～图3(i)可以看出,在θ∈[0.1,0.5]范围内,随着θ的增大,TTDTrust算法的MAE值、F值变化较小,而在θ=0.5后,MAE值显著增大、F值显著减小。这说明信任阈值θ不能设置过大,原因是信任阈值太大会导致太多的路径被剔除,即信任阈值过大将导致source获得过少关于target的信息,以至于降低了TTDTrust算法的精度。此外,从图3(i)可以看出,随着θ的增大,TTDTrust算法的运行时间变化甚微。

综上可知,k、L和θ对TTDTrust算法均有较大影响,尤其在k∈[3,9]、L∈[2,6]、θ∈[0.5,0.9]范围内影响较显著。从实验结果可以看出,在实际应用中取k=9、L=6和θ=0.5时,算法效果较好。

3 结束语

本文综合考虑网络中的节点拓扑结构信息和用户信任率信息,提出一种针对大规模社交网络的用户信任度预测算法TTDTrust,并设计一种用户拓扑信任度指标来衡量用户信任信息。在真实的社交网络分析数据集上进行多方面的实验测试,结果表明,与典型算法Tidal Trust、SWTrust相比,TTDTrust算法具有较高的信任预测精度和计算效率。由于实际社交网络往往具有较复杂的网络环境,且用户信任的影响因素较多,因此下一步将考虑多因素的信任建模并构建可应用于复杂网络环境的信任模型。