侧面角焊缝连接轴心受力板件的剪切滞后模型及设计建议
2018-08-17钟炜辉郝际平
钟炜辉,谭 政,郝际平
(西安建筑科技大学 土木工程学院,陕西 西安 710055)
在钢结构连接节点中,通常很难做到构件截面各部分都直接相连来传递内力,因此剪切滞后(Shear Lag)现象普遍存在.剪切滞后会使非全截面连接构件在连接节点附近仅有部分截面直接承受荷载,产生了应力不均匀分布的现象,截面强度不能充分发挥.我国现行《钢结构设计规范》GB50017-2003[1]并未就此问题进行规定,仅对偏心受力角钢对应的强度设计值进行了折减.美国规范ANSI/AISC360-10[2]、加拿大规范CAN/CSA-S16 -01[3]、澳大利亚规范AS4100[4]等国外标准对剪切滞后的影响却进行了详细规定,通过引入剪切滞后系数来对构件截面面积进行折减,进而对构件强度进行设计.
关于剪切滞后方面的研究,主要集中在轴心受力构件上,最早是上世纪初McKibben[5]所进行的有关工作,而其后最具代表性的是Chesson和Munse[6-7]根据试验数据总结出来的剪切滞后系数表达式,该表达式已被如ANSI/AISC360-10、CAN/CSA-S16-01等国外标准所采用.此后,Easterling和Gonzalez[8]、Petretta[9]、Bauer和Benaddi[10]、Zhu和Yan[11]等学者进行了大量的研究工作,对剪切滞后系数的表达式及相关计算标准进行了改进.由于影响剪切滞后现象的因素有很多,理论分析比较复杂,因此,上述研究工作大多基于试验研究,通过对试验数据的整理和分析获得相应的剪切滞后系数.在理论分析方面,最具价值的是Abi-saad和Bauer[12]首次基于广泛应用的Whitmore[13]应力扩散概念,建立了焊接构件剪切滞后的分析方法,该方法简单实用,物理意义明确.但遗憾的是,文献[12]并未就应力扩散角这一关键参数进行讨论,也未进行适当的数值分析来验证方法的正确性和适用性,存在着较大缺陷.
侧面角焊缝是轴心受力板件连接的典型形式,但由于以往对剪切滞后现象的研究多集中在螺栓连接,对焊接情况分析较少,因此相关标准[2,3]都是基于螺栓连接结果进行套用,从试验结果来看,计算公式偏于保守[8].根据文献[12]的基本思想,本文建立针对侧面角焊缝连接轴心受力板件的弹性和弹塑性剪切滞后模型,并结合数值模拟,可较为准确地获得危险截面上的正应力分布.通过与国外相关标准、试验数据进行对比分析,结合危险截面的塑性区范围,提出了剪切滞后系数的实用计算公式,以便工程设计应用.
1 剪切滞后模型
1.1 弹性剪切滞后模型
1.1.1 半无限板的弹性模型
如图1所示侧面角焊缝连接轴心受力板件(焊缝长度为L,板宽为2w,板厚为t,承受拉力2t),可近似认为焊缝处剪力沿焊缝全长均匀分布[1,12],此时每一个焊缝单元dx所承受的剪力(剪力流)为:
(1)
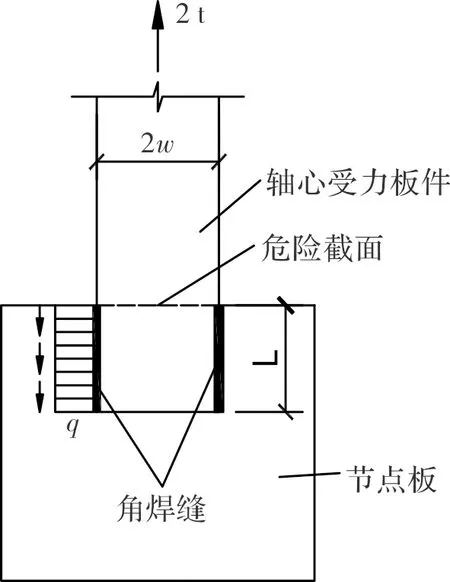
图1 侧面角焊缝连接轴心受力板件Fig.1 Axial forced plate with side fillet weld connection
当板件发生强度破坏时,板件内力最大的危险截面位于焊缝端部,同时由于剪切滞后的影响,危险截面上的正应力分布不均匀(大体上离焊缝越远,应力越小).因此,基于Whitmore应力扩散概念[13],可认为每一个焊缝单元上的剪力流会以应力扩散角θ传至危险截面,如图2a所示.每一个焊缝单元剪力传递到危险截面的正应力为:
(2)
用y1轴表示求焊缝单元所产生正应力时的坐标轴,y轴表示求焊缝所产生总正应力时的坐标轴,且有关系y1=xtanθ、dy1=dxtanθ,此时可将式(2)改写成:
(3)
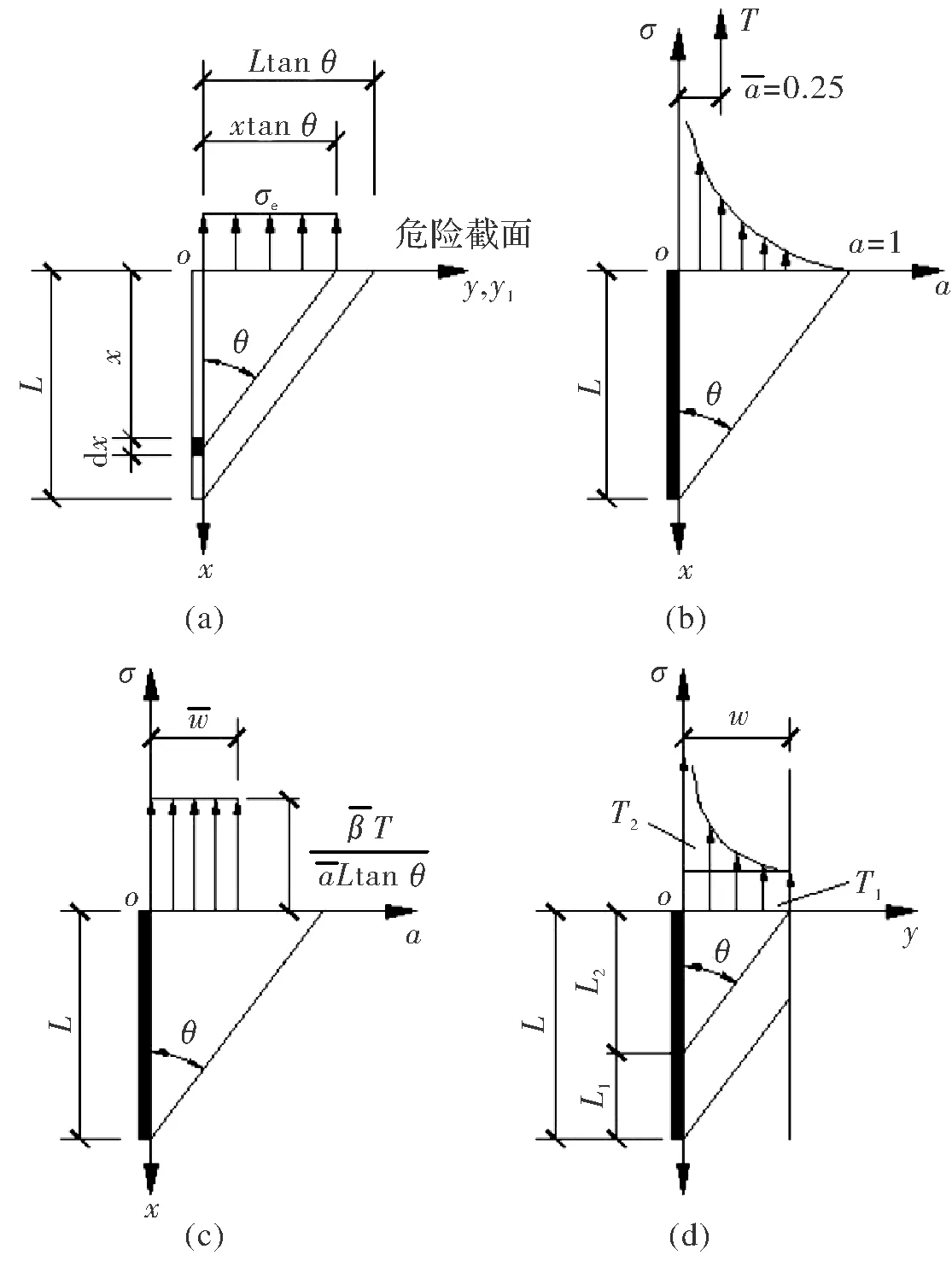
图2 侧面角焊缝的应力传递Fig.2 Stress transfer of side fillet weld
危险截面处的正应力应等于焊缝各单元所传递的正应力之和:

(4)
令σavg=T/(tLtan)、α=y/(Ltanθ),则可将式(4)简化为
(5)
上式:当α=1时,σ=0;当α=0时,σ→∞.由式(5)所得的危险截面应力如图2(b)所示,越靠近焊缝处正应力越大.正应力合力T的作用位置可由式(5)求得:
(6)
即合力点位置在距焊缝端处0.25Ltanθ,如图2(b)所示.显然,合力点位置左侧部分的较小截面承担较多的荷载.若定义应力图中某一位置点α′左侧部分截面承担的荷载占总荷载的比例为,则有:
(7)
(8)
1.1.2 轴心受力板件的弹性模型
上述所得结果以半无限板为依据,而实际使用的侧面角焊缝连接轴心受力板件为有限板,一般都满足2w/L≤1.0的构造要求[1],否则应增设正面角焊缝(或槽焊、塞焊).同时,板件全截面承载力一般不低于角焊缝连接承载力,大多满足w/L>0.2.因此,本文主要考察的板件尺寸范围为0.5≥w/L≥0.2.显然,当时,实际板件危险截面上的应力分布将变成如图2(d)所示,不能直接采用式(5)计算,而应将角焊缝承担的总荷载T分解成两部分,按叠加原理进行分析:
(9)
式中:L2=w/tanθ,L1=L-L2.T2(焊缝L2部分)在危险截面上产生的应力仍可按式(5)进行计算,而基于Whitmore应力扩散概念,T1(焊缝L1部分)在危险截面上产生的应力则是均匀的,T1和T2所占的比例大小主要取决于应力扩散角θ.关于应力扩散角θ的取值,文献[12]直接采用30°,从计算结果与试验数据的对比看,很不理想.实际上,应力扩散角θ并非常量,与w/L有关.
1.2 弹塑性剪切滞后模型
按弹性分析结果,危险截面靠近焊缝处的正应力将无限大,这显然与事实不符,因此有必要对危险截面的应力分布作弹塑性修正.为简化理论分析,材料采用理想弹塑性本构模型,屈服强度为fy.
侧面角焊缝连接轴心受力板件在危险截面上的弹塑性应力可假设为如图3(a)所示的分布形式(阴影部分),并类似按弹性模型的做法,划分为三个区域,分别由荷载T1、T2、T3产生.其中,T1在整个区域w上产生均匀应力f1,T2在塑性区域wp上产生均匀应力f2=fy-f1,T3在弹性区域we上产生弹性应力(仍遵循式(5)的分布规律,产生的最大应力为f2,位于点B处).为获得T3产生的弹性应力分布情况,采用坐标系σ3-o3-y进行应力等效,并假定图3(b)中的两阴影部分面积相等,由此可确定采用式(5)计算T3产生应力时的平均应力σavg为:
(10)
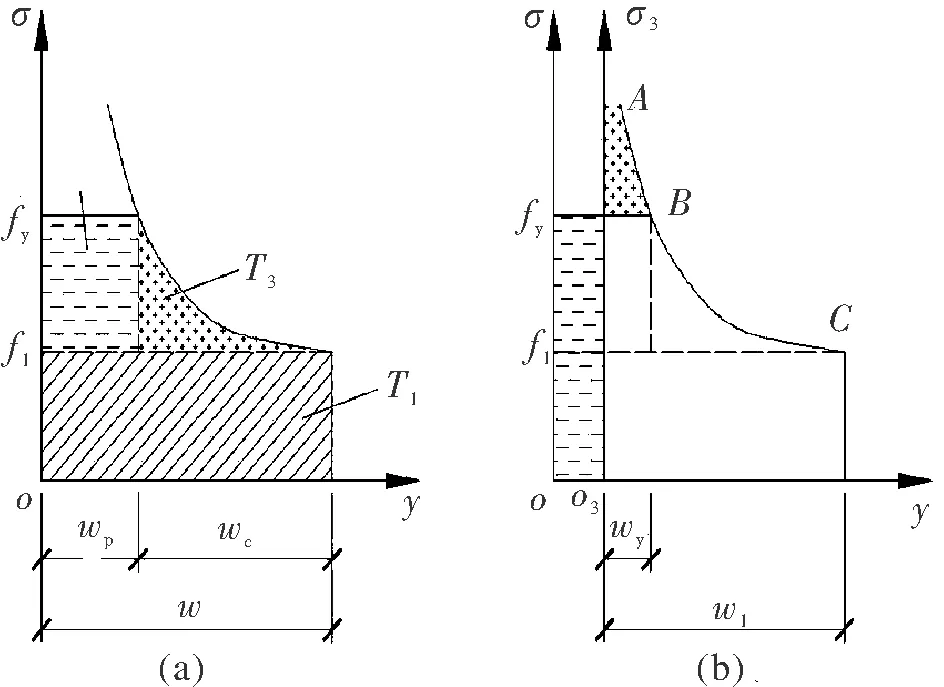
图3 弹塑性正应力分布Fig.3 Elastic-plastic normal stress distribution
由此,危险截面上的弹塑性应力可通过下列公式计算:
当0≤α≤αp时(塑性区)
σ=fy
(11a)
当αp≤α≤1时(弹性区)
(11b)
式中:α=y/w,α1=w1/w,αp=wp/w,αy=wy/w.当α=αp时,式(11b)应满足σ=fy,可得关系:
αy=α1e-f2/σavg
(12)
此时有:
αe=α1-αy=α1(1-e-f2/σavg)
(13)
根据式(11b)、(12)以及图3(b)所示的应力分布关系,可得:
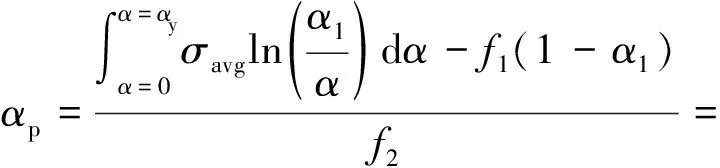
(14)
将式(13)、(14)代入αe+αp=1,得:
(15)
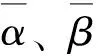
2 试验研究与数值模拟
早期最具代表性的针对侧面角焊缝连接轴心受力板件而开展的剪切滞后试验研究工作,是由美国焊接协会(AWS)在1931年完成的,但限于当时的焊接工艺水平,试件大多发生的是连接焊缝破坏而非板件拉断,而仅有成功的试件由于试验结果离散性大,不足以说明问题.随后,Easterling和Gonzalez[8]就受拉焊接构件的剪切滞后现象进行了27个试件的相关试验研究工作,实测钢材的弹性模量为199 800 MPa、屈服强度为358 MPa、极限抗拉强度为503MPa.其中,侧面角焊缝连接轴心受力板件试件7个(6个试验成功,1个试验加载没破坏),试验值如表1所示.试验中的剪切滞后系数是按构件被拉断来定义的:
(16)
式中:Pu为试件的受拉破坏荷载;An为试件的净截面面积;fu为材料的极限抗拉强度.

表1 试验结果Tab.1 Experimental results
注:(1)截面2PL 76.2×6.35表示板宽为76.2 mm、板厚为6.35 mm的双板;(2)表中Pt为试件的受拉破坏荷载.
为进一步分析剪切滞后对轴心受力板件强度的影响,采用通用有限元程序ABAQUS进行数值模拟分析,钢材采用线性强化本构模型(相关参数取试验实测材性数据[8]),泊松比为0.3.焊缝断面简化为等边直角三角形,与钢材采用绑定方式以模拟焊缝连接,连接板和节点板采用法向硬接触,设定最大位移为2 mm,有限元模型如图4所示.

图4 试件有限元模型Fig.4 Finite element model of test specimen
图5为表1中P-L1系列试件(w/L=0.353)连接处的应力分布云图,可见在关键截面处应力沿板宽分布不均匀,大致呈两端大中间小的分布趋势,试件破坏为关键截面在连接板与焊缝相连的小部分区域由于出现应力集中而发生局部受拉破坏,这与前述的理论分析和试验现象一致.
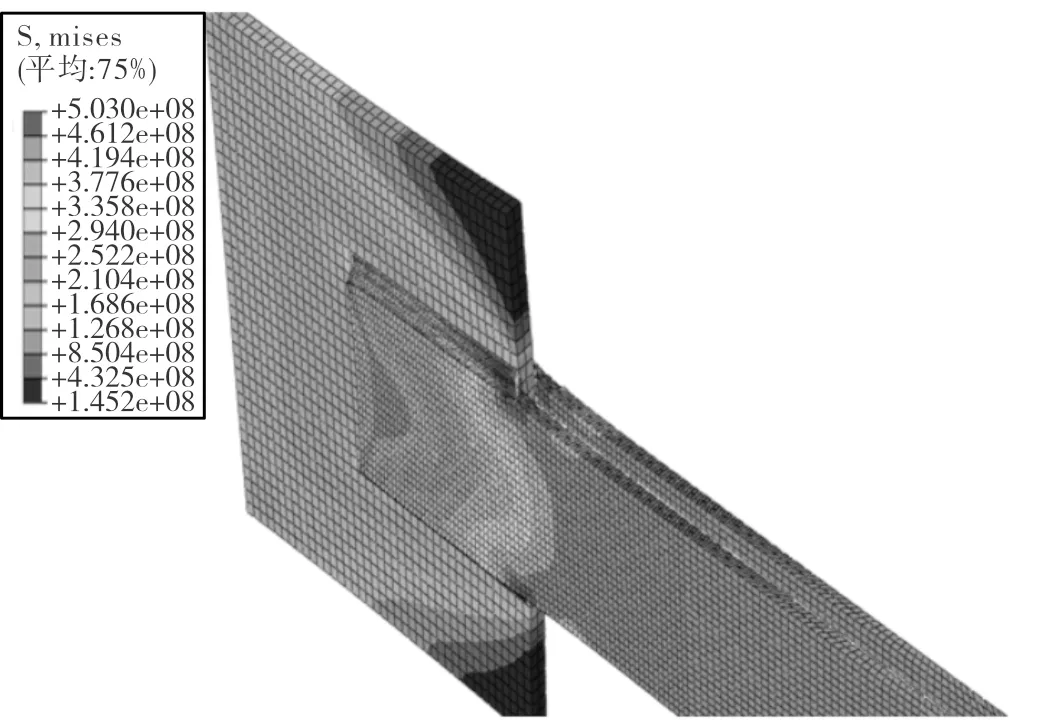
图5 P-L1试件连接处的应力分布Fig.5 Stress distribution at the joint of P-L1 specimen
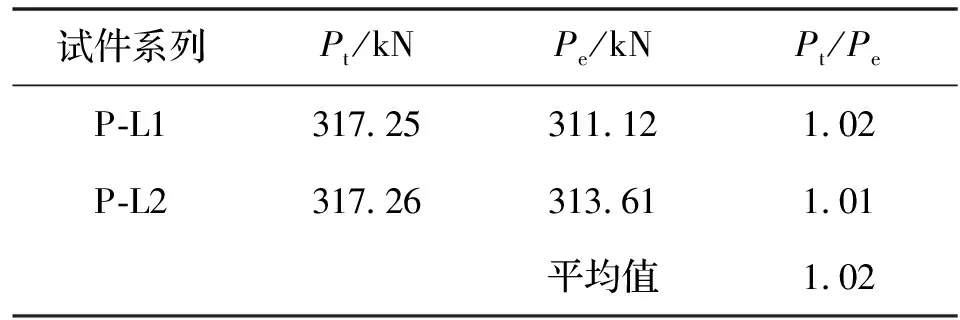
表2 试验值与计算值对比Tab.2 Comparison of test data and calculated value
注:Pe为以最大应力达到极限抗拉强度为破坏标志的数值分析结果.
表2列出了数值分析结果与试验结果,并进行了比较,总体误差约2%,吻合较好,可见有限元模型有较高的计算精度,能很好地模拟侧面角焊缝连接轴心受力板件的受力情况.
3 弹塑性计算及应力分布
应用弹性和弹塑性剪切滞后模型对侧面角焊缝连接轴心受力板件进行分析计算时,尚需确定应力扩散角θ这一关键参数.
3.1 弹性分析计算
弹性状态下不同w/L下的数值计算结果如表3所示,通过拟合,建议当应用弹性剪切滞后模型(如图2(d)所示)时,应力扩散角θ可按下式简单得到:
(17)
式中:δ为应力扩散系数,代表了T2所占总荷载的比例,当w/L=0.5时δ=0.26,当w/L=0.2时δ=0.20,当0.5>w/L>0.1时δ采用线性插值确定(即应力扩散角θ在63~45°之间变化).
由式(17)计算得出的结果也列于表3,表明式(17)所获得的应力扩散角θ具有足够精度.当w/L为0.5和0.25时,由数值计算以及弹性模型所获得的危险截面正应力分布如图6所示,二者十分吻合.
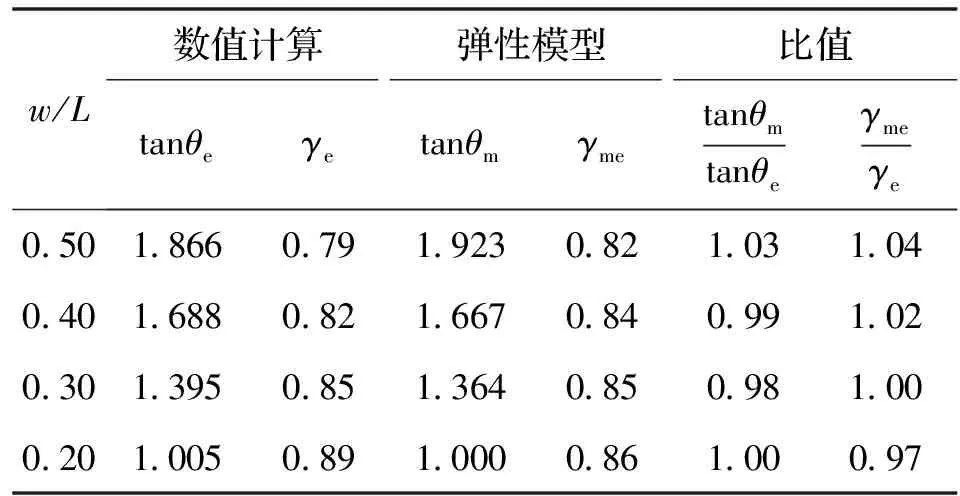
表3 弹性分析计算结果Tab.3 Calculation results of elastic analysis
注:tanθm由式(17)计算确定.
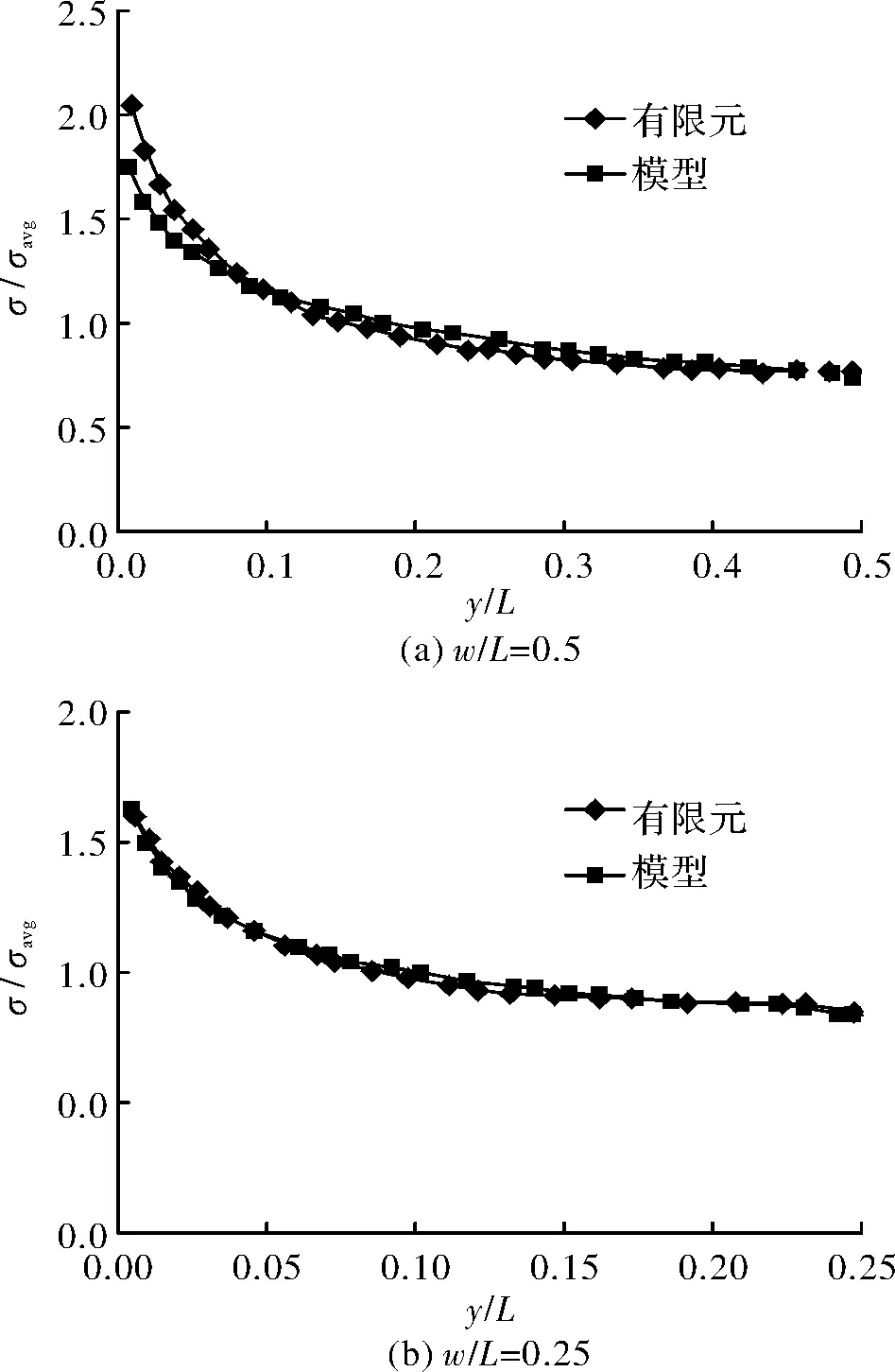
图6 危险截面的正应力分布Fig.6 Normal stress distribution at critical section
3.2 弹塑性分析计算
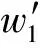
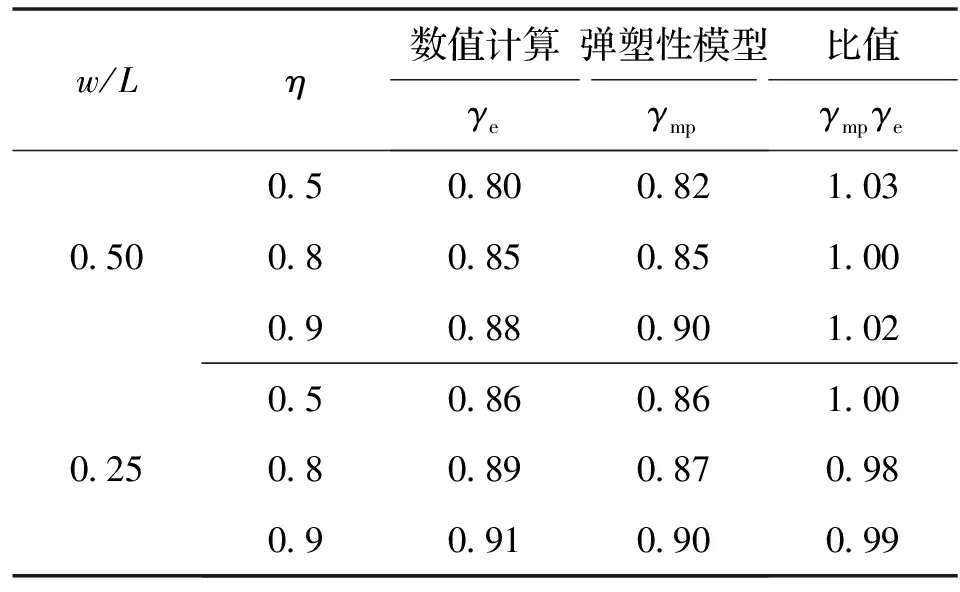
表4 弹塑性分析计算结果Tab.4 Calculation results of elastic-plastic analysis
当w/L为0.5和0.25时,在荷载系数η=0.9下危险截面的弹塑性正应力分布如图7所示,可以看出,实际塑性区的应力状态是比较复杂的,虽然计算中假定材料为理想弹塑性材料,但危险截面上的塑性区其正应力大多已超过屈服强度fy.
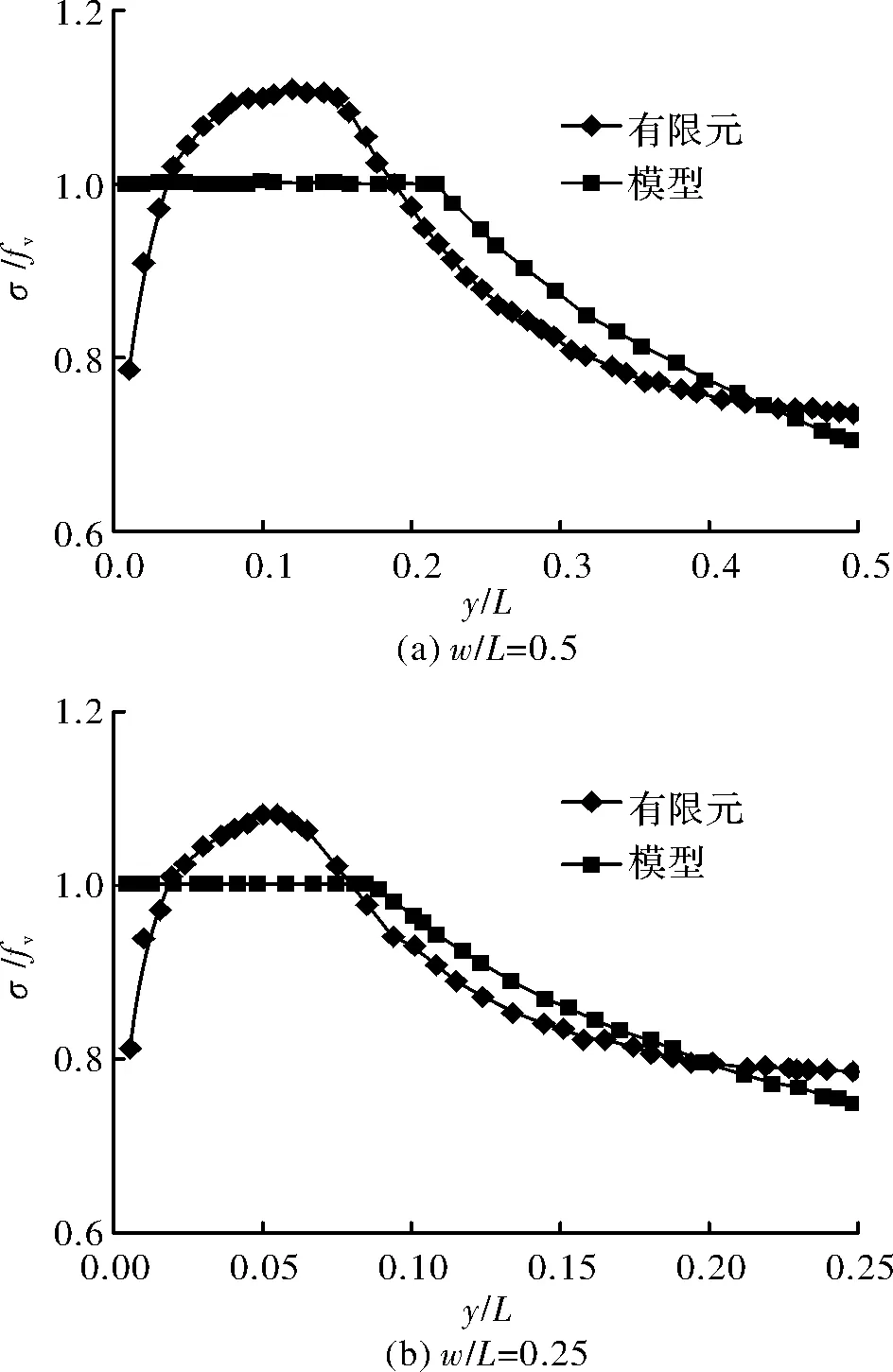
图7 危险截面的弹塑性正应力分布(η=0.9)Fig.7 Elastic-plastic normal stress distribution at critical section(η=0.9)
4 剪切滞后系数实用计算公式
剪切滞后系数γ反映的是实际参与承担荷载的板件截面面积,当η=γ时,可认为其有效承载截面均发生了屈服,达到其承载能力极限状态,此时的剪切滞后系数γ在设计中可看作是考虑剪切滞后的截面折减系数.
表5列出了不同w/L下基于前述弹性和弹塑性模型的剪切滞后系数,可以看出,由于弹性计算中未考虑部分截面屈服而产生的应力重分布影响,因此所得的剪切滞后系数都比弹塑性结果小,且当弹塑性η=γ时,板件危险截面约有一半区域进入塑性.另外,表5也列出了美国和加拿大规范对剪切滞后系数的取值,以及由弹塑性模型反算出来的塑性区范围(当η等于相应剪切滞后系数时),可见随着w/L越大,美国和加拿大规范的剪切滞后系数取值更偏向于弹性,对塑性区的发展要求更严格.相比较而言,美国规范更保守.
综合考虑危险截面的弹塑性应力分布和塑性区发展情况,本文建议对侧面角焊缝连接轴心受力板件,可按以下简化公式计算剪切滞后系数:
(18)
上式的应用范围为0.5≥w/L≥0.2.对强度较高的钢材,式(18)的计算结果应进行折减,以考虑由于材料塑性性能的降低使剪切滞后现象趋于严重.根据文献[14]的分析结果,该折减系数的取值范围大概在0.6~1.0之间.
表6列出了表1试验结果和美国、加拿大规范以及式(18)关于侧面角焊缝连接轴心受力板件的剪切滞后系数取值,可见式(18)与试验结果更相符,并对w/L较大的情况,适当提高了安全度,可有效避免焊缝连接处板件局部发生过大的塑性变形.
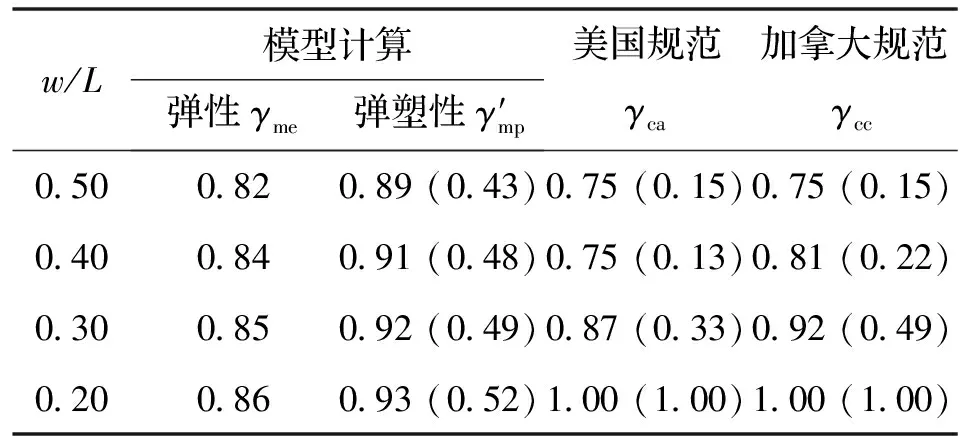
表5 剪切滞后系数及塑性区范围Tab.5 Shear lag coefficient and plastic range


表6 剪切滞后系数的取值比较Tab.6 Comparison of shear lag coefficients
注:γt为表1试验结果按式(16)计算得到的剪切滞后系数.
5 结语
基于应力扩散概念,对危险截面进行应力分析,建立了针对侧面角焊缝连接轴心受力板件的弹性和弹塑性剪切滞后模型;结合数值模拟,通过应力扩散角的计算可较为准确地获得危险截面上的正应力分布;通过与国外相关标准、试验数据进行对比分析,结合危险截面的塑性区范围,提出了剪切滞后系数的实用计算公式,以便工程设计应用.
致谢:本文的撰写得到了西安建筑科技大学陈绍蕃教授的指导和帮助,在此表示衷心感谢!
