拟牛顿迭代方法初始值的研究

张安玲

(长治学院 数学系,山西 长治 046011)

0 引言

拟牛顿法(Quasi-Newton Methods)是求解非线性优化问题的一种有效方法之一，它最大的优点是在参数初始值选择恰当的情况下，收敛速度快，精确度高[1].但是其收敛性和性能在很大程度上要依赖于初始值的选取[2].如果拟牛顿法选取的迭代初始值接近真实解，则容易找到最优解，并且具有局部快速收敛的优点，拟牛顿法会表现出较强的搜索能力；如果初始值离最优解较远，拟牛顿法运行通常失败[3]，所以提供好的初始值对于拟牛顿法来说是非常重要的.

粒子群优化算法，具有较强的全局搜索能力，但粒子群优化算法的局部搜索能力较差，当搜索到达真实解附近时，其搜索速度明显减慢甚至终止[1-3].

针对拟牛顿法和粒子群优化算法的特点，对所求问题在可行解区域范围内进行大范围的搜索，等进化到一定程度，把当代的最好点作为拟牛顿法的初始点，再运行拟牛顿法.这样，粒子群优化算法就能给拟牛顿法提供好的初始值，从而解决拟牛顿法对初始值的敏感问题，保证拟牛顿法的成功，同时加快搜索速度，提高解的精度.

1 算法设计

在非线性优化问题中，为了解决拟牛顿法的初始值问题，提出以下算法.

算法的主要步骤：

Step1粒子群优化算法运行M代；

Step2以Step1返回的当前全局最优个体作为拟牛顿法的初始值x(1)∈Rn，允许误差ε>0；

Step3置H1=In(单位矩阵)，计算出在x(1)处的梯度g1=f(x(1))，置k=1；

Step4 令d(k)=-Hkgk；

Step5 从x(k)出发，沿方向d(k)搜索，求步长λk，使它满足

令

x(k+1)=x(k)+λkd(k)；

Step7 若k=n，则令x(1)=x(k+1)，返回Step3；否则，进行Step8；

Step8 令

gk+1=f(x(k+1))，p(k)=x(k+1)-x(k)，q(k)=gk+1-gk

利用

计算Hk+1，置k:=k+1，返回Step4.

该算法是由粒子群优化算法和拟牛顿法结合而成.算法流程是先让粒子群优化算法运行M代，把当代的最好点作为拟牛顿法的初始值，然后循环执行拟牛顿法，直到达到要求精度或达到最大迭代数停止.

粒子群优化算法是给拟牛顿法提供好的初始点，并没有改变原拟牛顿法的收敛性，所以本文算法具有与原拟牛顿法相同的收敛性.

2 数值计算与分析

选取三个典型函数对该算法进行验证：

利用本文算法对以上测试函数进行数值仿真计算，计算结果见表1.

从表1可知，对一般优化方法难以优化的F1～F3函数，本文算法都以100%的概率成功地找到了全局最优解，并且求解精度高、运算速度快.

表1 本文算法对F1～F3的数值结果

当M=1时，粒子群优化算法运行1次，然后就开始执行拟牛顿法，此时粒子群优化算法的作用相当于给拟牛顿法随机提供一个初始值.所以当M=1时，本文算法退化为一般的拟牛顿法.

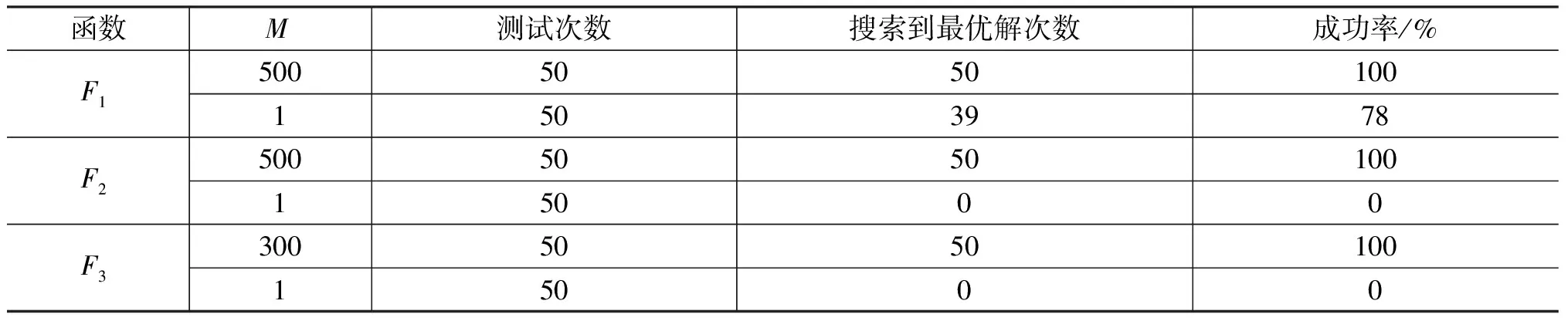
表2 本文算法和拟牛顿法的比较

注：M=1表示拟牛顿法，M=500或300表示本文算法；精度达到10-12认为算法成功.

从表2可知，对函数F1，拟牛顿法的成功率是75%，但对有大量局部极小点的多峰函数F2与F3，拟牛顿法就完全运行失败.其主要原因是拟牛顿法只具有局部搜索能力，并且在没有被赋予好的初始值时，算法的成功率很低.其原因是拟牛顿法没有全局搜索能力而且对初始值非常敏感，在没有被赋予好的初始值时，算法往往失败.而本文算法的成功率达到了100%，这充分说明粒子群优化算法为拟牛顿法提供了很好的初始值，从而保证了拟牛顿法的成功.

为了进一步了解粒子群迭代数M对拟牛顿法的影响，以函数F3为例进行分析.具体见表3.

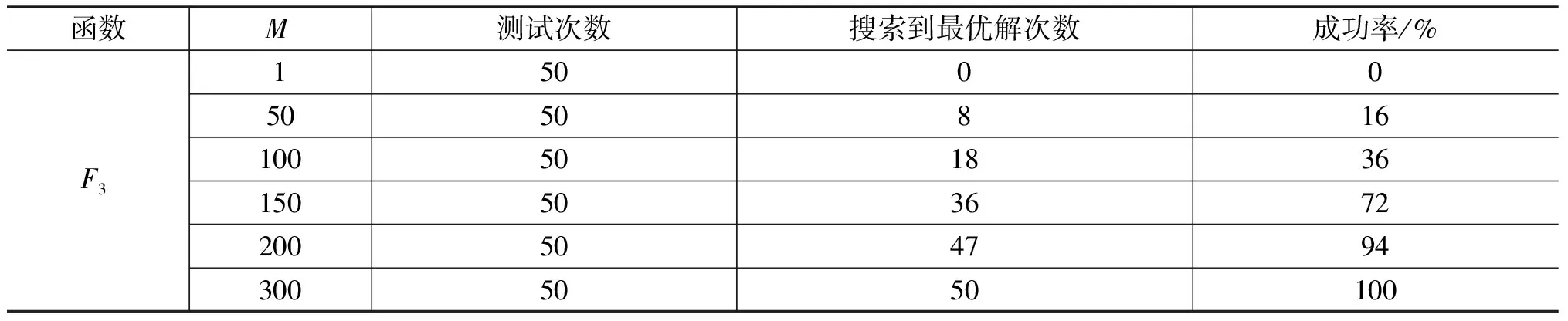
表3 不同初始值对拟牛顿法的影响

注：精度达到10-12认为算法成功；M取值越大，提供给拟牛顿法的初始值越好.

从表3可知，当M=1时，算法的成功率是0%，表明使用拟牛顿法的失败率是100%；当M的取值增大时，算法的成功率也在增大.这是因为：当M取值较小时，粒子群优化算法迭代次数少，获得解的精度低，也就是传给拟牛顿法迭代的初始值较差，拟牛顿法在没有获得好的初始值情况下运行失败；相反，当M取值较大时，粒子群优化算法迭代次数多，获得解的精度相对高，从而传给拟牛顿法的初始值较好，此时，拟牛顿法就可以充分发挥它的局部精细搜索性，所以成功率比较大.这充分表明先运行若干代粒子群优化算法，然后把当代最好点作为拟牛顿法的初始值，这种做法能有效解决拟牛顿法的初始值问题，从而保证拟牛顿法的成功率.

3 结束语

本文提出了一种为拟牛顿法提供好的初始值的方法.该方法首先是粒子群优化算法在可行解区域范围内用随机选取的初始值运行若干迭代，把得到的最好解作为拟牛顿法的初始值，然后拟牛顿法利用这组初始值进行迭代搜索.实验结果表明，该方法为拟牛顿法提供了较好的初始值，从而有效地解决了拟牛顿法对初始值敏感的问题，在很大程度上提高了拟牛顿法的成功率.另外，本文算法并没有改变拟牛顿法的收敛性，具有与原拟牛顿法相同的收敛性.