多无人平台持续作业调度问题
2018-08-16宋志强周献中
宋志强,周献中
(1.南京大学 工程管理学院,南京 210008;2.苏州经贸职业技术学院 机电与信息技术学院,浙江 苏州 215009)
2012年,美国空军学院开始进行一项“无人系统协同技术”的研究工作,进行不同类型多无人平台协同目标跟踪的研究,将探索融合无人平台不同类型传感器的数据,以提高地理定位移动目标的准确性,加强作战优势。无人平台(Unmanned Vechile,UV)可分为无人机(Unmanned Aerial Vehicle,UAV)、无人车(地面无人平台)(Unmanned Ground Vehicle,UGV ) 和无人艇 (Unmanned SurfaceVehicle,USV)等。自1917年英国人研制出世界上第1架无人机,无人机经历了近百年的发展历程。无人机在海湾战争、科索沃战争、阿富汗战争、伊拉克战争和利比亚战争中广泛使用并表现优异,世界各军事强国都在积极研制本国的无人机[1]。2011年2月和4月,美国高智能化的作战型无人机诺斯罗普·格鲁门X-47B、“幽灵射线”无人战斗机完成首飞;2014年,美国多次出动无人机空袭IS极端武装。无人机除在军用方面,在民用方面也具有其潜在的应用,如灾难拯救、智能视频监控、海上搜救和空间探测等。地面无人平台就是在地面上行驶的能执行特定任务的机器人,是机械化、信息化、智能化高度融合的机动平台。地面无人平台技术除军事应用外,在民用方面也具有非常广阔的应用前景,如许多高温、高寒、荒漠区域,需要地面无人平台探测开发;另外,工业制造、农耕作业、科学考察、抢险救灾、排爆、救援以及交通运输等领域都需要智能化的地面无人平台。
单无人平台由于其视线遮挡、运动限制、能量受限等因素,常常不能实现对目标进行连续作业,因此需要多无人平台协作以维持对目标的持续作业,从而获得更好的效果。多无人平台在发现、跟踪目标和搜救等方面具有重要的应用价值,如可对目标持续监视、跟踪,以防止目标失联。由于燃料或电池容量问题,无人平台的续航时间常受到限制。在没有后勤保障的情况下,无人平台的持续作业能力是其应用的瓶颈,如果无人平台具有良好的持续作业能力,那么,无人平台的服务能力将显著增强。配备有能够完成无人平台加油、电池更换或充电等操作的自动补给站的多无人平台系统使无人平台持续作业成为可能。当一个无人平台能量不足时,其可将任务移交给其他能量充足的无人平台继续执行任务,而能量不足的无人平台从附近的自动补给站寻求补给。本文考虑未来将多无人平台应用于需要持续作业的应急救援场合,建立问题模型,通过多无人平台和自动补给站的调度,实行多无人平台系统的持续作业。
无人平台中的无人机是目前主要的研究对象,多无人机协同问题研究是当今研究热点,主要涉及协同侦察、协同搜索、协同探测与感知、协同任务规划、协同跟踪、协同路径跟随与编队控制等问题。文献[2]中研究多无人机协同侦察问题,文献[3-5]中研究多无人机协同搜索问题,文献[6-7]中研究协同多无人机探测与感知问题。对于协同跟踪问题,目前研究最多的一类协同跟踪为协同对峙跟踪[8-9]。文献[10]中介绍了空中和地面机器人协同工作以完成火灾监测和灭火任务,并描述了系统架构。文献[11]中研究在动态不确定环境下多无人机实时任务
分配问题。文献[12]中将多无人机任务规划问题建模为标准车辆路由问题。文献[13]中研究了任务同步情形下的无人机资源调度问题。上述文献均未考虑无人机的能量约束问题。文献[14]中开发了为无人机补给的自动服务站,使多无人机持续作业成为可能。文献[15-17]中研究了多无人机持续作业问题,但系统考虑仅存在一个具有多端口的服务站情形,即没有考虑存在地理上分散的多个服务站的问题。文献[18]中研究了具有地理上分散的自动补给站支持的多无人机持续作业问题,仅将多无人机的总飞行距离作为目标函数,没有考虑各无人机的出行成本。
文献[18]中提出的模型目标函数仅是最小化总距离,即只考虑同构平台,而由于异构无人平台构成的系统更具普遍意义。因此,本文考虑由于无人平台型号、功能等的不同,引起的无人平台出动成本的不同,将其也纳入目标函数;同时,考虑无人机的飞行距离与出行成本,更符合实际情况。
1 情景想定
鉴于已有电池更换系统[19]应用于无人机,在此假想未来多无人机系统在执行应急任务时,具有地理位置分散的自动补给站作为后勤保障,无人平台在自动补给站可完成加油或电池更换等能量补充,也可在自动补给站装配应急物资等,以便多无人平台能够持续、不间断地完成任务。图1为具有3个补给站、4架无人机和3个目标的示例系统。
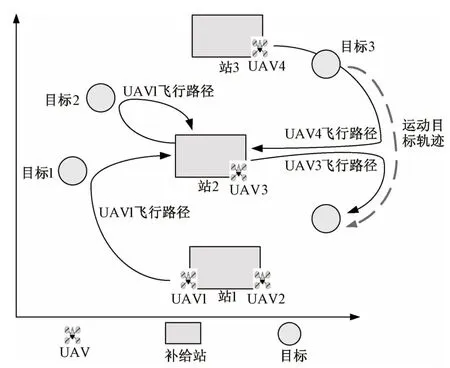
图1 具有3个补给站、4架无人机和3个任务的示例系统
为了解决无人平台能量有限的问题,本文提出多无人平台共享地理上分散的自动补给站的思想,设计调度算法来协调任务。假定无人平台要完成的任务的时空轨迹是确定的,至少有一个无人平台执行任务。如图1所示,多无人机系统任务是为时空轨迹确定的3个目标提供不间断的服务,其中目标1和目标2是静止的,均为待无人机服务的应急需求点。3个候选自动补给站分布于任务空间,它们可被任一无人机使用。其中的一个可行方案为UAV1从自动补给站1出发,先向目标2提供服务;然后飞至自动补给站2补充能源和资源,之后飞至目标2提供服务;最后,返回自动补给站2。无人机的另一任务是对运动目标3进行护航或跟踪,由于运动目标3的路径持续时间大于无人机的最大飞行时间,则首先由UAV4提供服务,在UAV4出现能量预警时,将其任务移交给UAV3,由UAV3完成剩余的服务,而UAV4 飞至自动补给站2 进行补给。在该方案中,UAV2不参与任务的执行。整个系统的协同可使得任务不中断的执行。
Kim 等[18]提出通过无人机和服务站的合理调度,可使无人机持续跟踪给定时空轨迹的思想。借鉴其思想,本文将具有确定性时空轨迹的任务分为多个子任务。由于油量或电池容量有限,单个无人平台可能不能执行整个完整的任务,故有必要将一个任务分为若干个子任务。如图2所示,根据运动目标的轨迹将任务分为若干子任务,每个子任务可由一个无人平台提供服务。由于假定目标的运动轨迹是确定的,故可获得每个子任务的开始和结束坐标,子任务i的起始和结束坐标分别为(x is,y is)、(x ie,y ie)。子任务的数量及其位置和时间可预先确定。用Dij表示子任务i的终点或自动补给站i至子任务j的起点或自动补给站j的欧式距离。
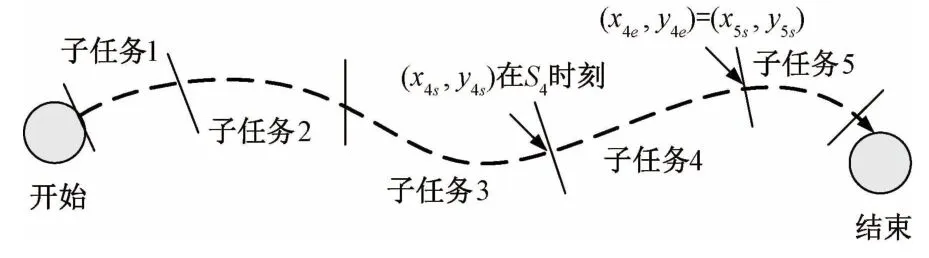
图2 将运动目标时空轨迹分为子任务
2 符号定义
各符号含义:
i,j——任务索引,i,j∈ΩJ={1,2,…,N J}
s——自动补给站索引
k——无人平台索引,k∈K={1,2,…,NUV}
l——无人平台第l次出行索引,l∈L={1,2,…,N L}
W t——无人平台单位距离行进成本
P k——无人平台出动成本
N J——系统中子任务数量
NUV——系统中无人平台数量
NSTA——系统中自动补给站数量
NL——无人平台出行最大次数
M——大正数
Dij——子任务i的终点或自动补给站i至子任务j的起点或自动补给站j的距离。注意,由于起点和终点的变化,故Dij不一定等于D ji
Si——子任务i的开始时间
Ei——子任务i的结束时间
H i——子任务i的处理时间(Ei-Si)
T——无人平台在自动补给站的补给时间
Qk——无人平台k的最大续航时间
Sok——无人平台k的初始位置
MSk——无人平台k的最大速度
ΩJ——子任务集,ΩJ={1,2,…,N J}
ΩSS——无人平台任务起始站集,
ΩSS={N J+1,N J+3,…,N J+2NSTA-1}
ΩSE——无人平台任务结束站集,
ΩSE={N J+2,N J+4,…,N J+2NSTA}
ΩA——所有任务和自动补给站集,ΩA=ΩJ∪ΩSS∪ΩSE
X ijkl——二进制决策变量,若无人平台k在第l次出行期间,在处理完子任务i或在站i完成补给后,处理子任务j或在站j补给,则为1,否则为0
Cikl——决策变量,若无人平台k在第l次出行期间,执行子任务i开始时间或无人平台k在站i补给开始时间,否则为0
3 建 模
在此,除考虑无人平台最大速度约束外,不考虑如无人平台的其他飞行动力学约束。本文将多无人平台的持续作业调度问题描述为混合整数线性规划(MILP),目标函数为最小化无人平台出行和出动总成本为:
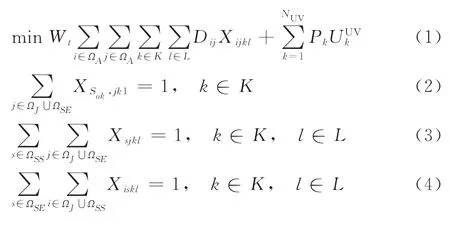
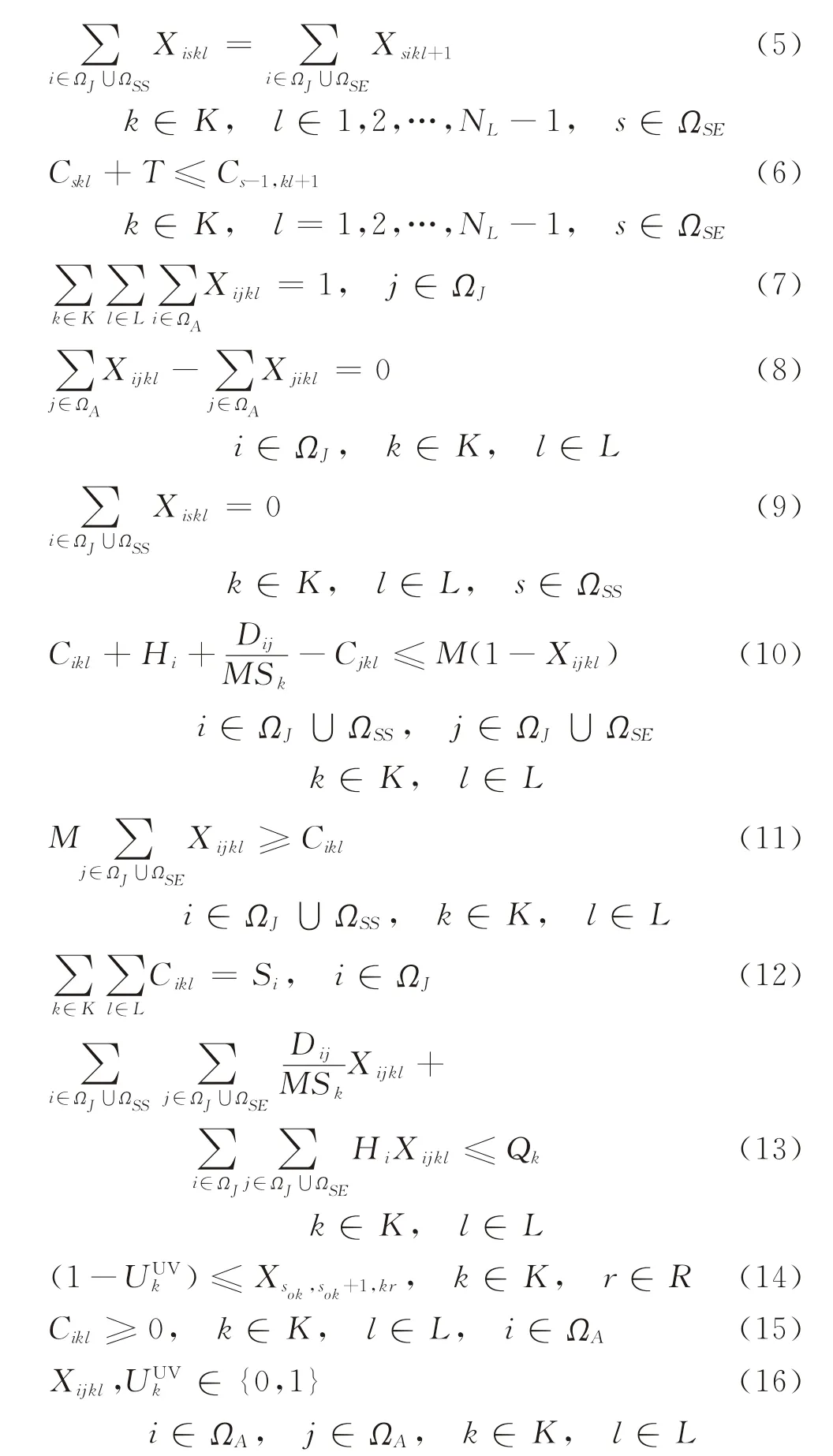
初始自动补给站约束式(2)确保每个无人平台从其初始自动补给站开始第一次作业。自动补给站约束式(3)确保每次作业无人平台k仅从一个自动补给站出发至子任务。式(4)确保无人平台k每次作业必须且仅在一个结束补给站完成。式(5)确保无人平台k第l次出行结束站和其l+1次作业起始站相同。式(6)表明,在同一自动补给站无人平台第l次出行完成时间与其第l+1次出行开始时间的关系。子任务分配约束式(7)确保在ΩJ集中的每个子任务都能由一个无人平台处理。式(8)确保无人平台不能在子任务上结束工作。式(9)确保无人平台不能在起始站(s∈ΩSS)完成作业,此约束来自于每个站有两个索引。开始时间约束式(10)给出了无人平台k第l次出行期间子任务i或站i的补给开始时间与无人平台下一步动作的关系。式(11)隐含信息为若子任务i未分配给第l次出行的无人平台k,则决策变量Cikl为0。式(12)保证在ΩJ集中的每个子任务均能在预先确定的开始时间被执行。能量约束式(13)表明,无人平台k的包括旅途时间和子任务处理时间在内的总出行时间不超过无人平台k的最大续航时间。被选中无人平台约束式(14)确保仅选中的无人平台去执行子任务。决策变量非负和整数约束式(15)、(16)限定的决策变量的取值范围。
由于式(5)、(6)的约束,该数学模型要求NL>1。NL只是无人平台出行最大次数,并不限制模型能力。文献[18]中使用决策变量Y ikl表示UAVk在第l次出行时,子任务i分配给UAVk,但该信息其实已经隐含在决策变量Cikl中,故可删除。本文所设计模型比文献[18]中的模型决策变量要少,从而减少了计算复杂度。若无人平台最大出行次数NL=1,则式(5)、(6)可删除。
4 算例求解
仿真试验在PC 机上运行,PC 机配置为Intel(R)Core(TM)2 Duo CPU E7200,2.52 GHz,2 GB内存,仿真软件采用MATLAB 2014a,利用该版本提供的Intlinprog 函数可较方便地求解MILP问题。
算例1假设有3 个任务需要无人平台来完成,其中任务1和任务2需要无人平台运送应急物资至指定位置处,任务1的坐标在(100,450)处,任务2的坐标在(150,100)处,任务3为无人平台跟随目标3运动轨迹,任务3起始坐标为(590,590),终止坐标为(590,11)。有3个候选自动补给站(Station),Station1 坐标为(50,200),初始有UV1和UV2,Station2的坐标为(500,600),初始有UV3和UV4,Station3 的坐标为(450,300),初始有UV5。系统初始部署图如图3所示。

图3 系统初始部署图
将3个任务分为6个子任务,假设每个子任务的处理时间均为2 min,子任务信息如表1所示,将任务3分解为子任务1、2、3、4。任务1、2即子任务5、6。
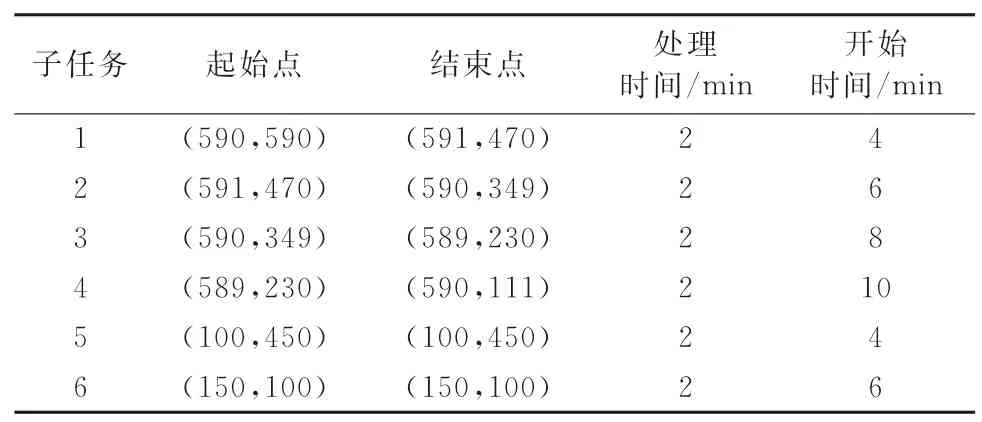
表1 算例1的3个任务分成6个子任务的信息
仿真参数表如表2所示。

表2 仿真参数表
将上述MILP问题在Matlab 2014a中求解,当无人平台的最大续航时间Qk=16 min时,UV1从自动补给站1出发,先执行子任务5(即任务1),接着执行子任务6(即任务2),然后返回自动补给站1;UV3从自动补给2站出发,依次执行子任务1、2、3、4,然后至自动补给站3。整个过程总费用为13 337.5元,期间UV2、UV4、UV5 不参与任务执行。由于Qk=16 min,UV3从自动补给2站出发,依次执行子任务1、2、3、4,返回自动补给站3,不违反式(13)的约束条件,故由UV3完成任务1。
当无人平台的最大续航时间Qk=8 min时,受式(10)约束,UV1从自动补给站1出发,执行子任务5(即任务1),然后返回自动补给站1;UV2从自动补给站1出发,执行子任务6(即任务2),然后返回自动补给站1。受式(13)约束,UV3从自动补给2站出发,执行子任务1、2后,然后至自动补给站3补给;UV5从自动补给3 站出发,执行子任务3、4后,返回自动补给站3。由于最大续航时间的约束,由子任务1、2、3、4组成的任务1由UV3、UV5协作完成,对于任务1而言,由于多无人平台的“接力”,弥补了单一无人平台由于能量有限而无法完成整个任务的缺点,实现了多无人平台持续不间断地作业。整个过程总费用为¥16 453,期间UV4不参与任务执行。
算例2假设由无人平台进行边境巡逻,自动补给站1 位于(300,600),自动补站2 位于(600,300)处,开始时UV1、UV2分别位于站1、站2,有4条巡逻路径需无人机遵循,各路径的起点、终点如图4所示。
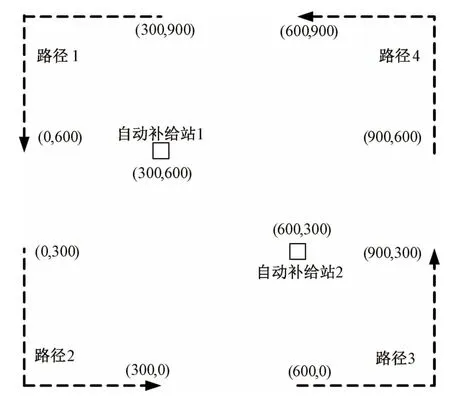
图4 无人平台边境巡逻部署图
路径1、2、3、4需分别于6、18、6、18 min开始,无人平台的最大速度为150 m/min,如表3所示,将整个巡逻任务分为8个子任务,各无人平台的最大续航时间Qk=15 min。
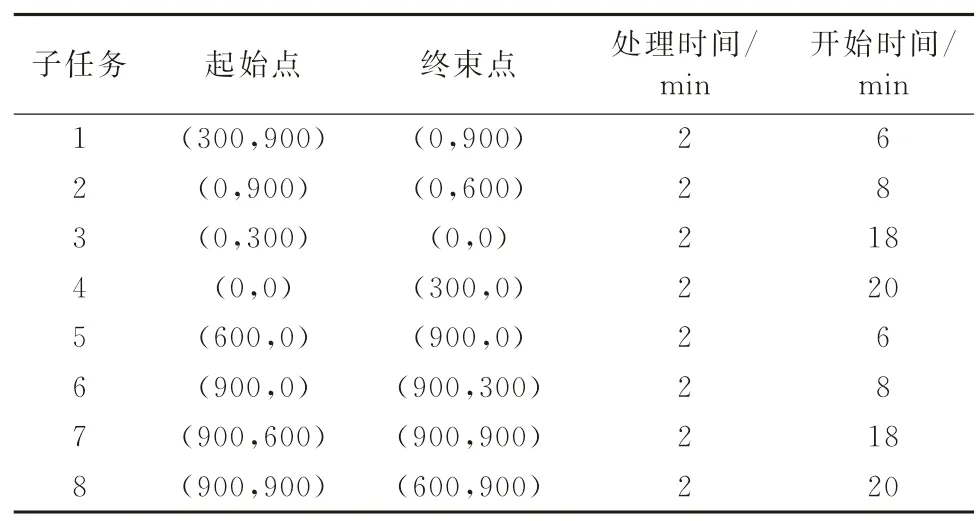
表3 算例2的8个子任务信息
W t=8 元/m,UV1 的P1=400 元,UV2 的P2=700元,用Matlab 2014a可求得最优解:UV1从站1出发,完成子任务1、2、3、4,然后进入站2补给。UV2从站2出发,完成子任务5、6、7、8后进入站1补给,整个过程总费用为27 088元。
5 结语
无人平台由于电池寿命或燃料量的限制,其应用受到制约,单一无人平台不能进行持续作业。具备地理上分散的自动补给站支持的多无人平台系统可完成持续时间长的任务。对于确定性任务而言,无人平台在作业时若能量即将耗尽,则可至附近自动补给站获得补给,而后再次作业或在自动补给站待命。同时,其他无人平台接替该无人平台的工作,继续任务的执行。通过自动补给站,任务可被多个无人平台以“接力”的形式不间断地执行。本文将多无人平台任务调度问题建模为混合整数线性规划(MILP)问题,并用Matatb 2014a求解实例。结果表明,多无人平台持续作业调度可提高系统的自主性和实用性。用启发式或智能算法来解决MILP问题[20]是今后该领域的努力方向。
