风洞模型支杆系统设计及振动主动控制
2018-08-16鲁继文刘巍刘昱贾振元刘惟肖张家昆姜雨丰
鲁继文,刘巍,刘昱,贾振元,刘惟肖,张家昆,姜雨丰
(1.大连理工大学机械工程学院,辽宁 大连 116024;2.航空工业空气动力研究院,辽宁 沈阳 110034)
0 引言
为了满足航空航天装备地面测试数据的准确性和可重复性要求,地面测试设备需要根据不同的环境进行不同程度的改进与提升。为了大幅度降低飞行器的开发时间和成本,在投入批量生产前,需要进行大量的风洞实验[1]。风洞实验是了解验证飞行器空气动力学特性的一种特殊实验方法,从实验中获取机型的各种参数数据。在风洞实验过程中,需要对飞行器进行支撑。主要支撑方式有背撑、腹撑及尾撑,还有另加张线或利用磁悬浮原理的支撑。而由于这些外加支撑的存在,飞行器的绕流场会与实际情况有较大差别。新一代飞行器多采用尾部支撑系统,由弯刀、支杆、测力天平和模型等相连组成,是一个典型的悬臂式结构。模型支杆的直径通常会使用允许的最小直径,从而减小空气动力干扰。同时为了减小姿态控制机构(弯刀)的气动干扰,支杆长度一般是模型长度的三到五倍,该几何结构使系统刚度较低[2]。而风洞实验时,模型受到宽频带的气动载荷激励,与支杆-模型系统一阶固有频率相耦合,将会导致模型在俯仰方向产生大幅、低频共振,在飞机大攻角实验中更为剧烈。不仅大大影响飞机测力数据的品质,而且还对模型及风洞的安全产生巨大的威胁。因此,抑制飞行器模型振动是当下急需解决的重大难题[3]。
目前常用的振动抑制方法主要有被动抑制和主动抑制两种。被动抑制需要人为添加振动能量吸收装置,这些装置可以是粘弹性阻尼器、调谐阻尼器,或者是流体阻尼器,也可以通过电气设备将振动能量耗散出去。1968年,美国航空航天局的William B. Igoe 等人提出了一种动态振动吸收器,实质为一调谐吸振型的被动抑振装置,通过调谐使其内部质量块与模型谐振,再由阻尼液体吸收振动能量。该装置能在俯仰方向实现抑制振幅的峰值和均方根值接近50%,但该装置在不同的实验条件(例如不同马赫数)下的性能相差较大。而主动抑制可以通过对振动的实时反馈,在支杆的某一段实时产生与模型端所受弯矩相反的动态力矩,从而达到实时抑制振动的目的。
在1996年,欧洲跨声速风洞(ETW)的G. Hefer提出了一种基于叠堆式压电陶瓷作动器的主动振动抑制方法。该装置由环布的六组作动器组成,在此基础上,H. Fehren等人于2001年改进了方案,将压电作动器的数量提高至14个,能够减弱除滚转方向外所有自由度的振动。实验结果表明,在气动激励不超过抑振系统功率上限时,振幅的抑制效果比较明显。美国NANA的S. Balakrishna等人于2007年也设计了一套基于压电陶瓷的抑振系统,并在针对某型号模型的一系列实验中,使模型在跨声速中的最大攻角从未安装抑振器时的6°提高至12°。而南京航空航天大学与中国空气动力研究发展中心合作也针对支杆振动问题进行了主动控制研究,并提出了相关的控制算法,在实验室中已经取得了初步成果,但是需要进一步在风洞实验中完善和改进。
由于堆叠式压电陶瓷有体积小、输出力大以及动作响应迅速等特点,广泛用于振动主动控制[4-5]。本文以堆叠式压电陶瓷作为作动器,设计搭建了一套尾撑式支杆模型振动主动抑制系统,在实验室实验中取得了很好的抑振效果。
1 振动抑制原理
风洞模型支杆系统是一个由飞行器模型、风洞实验天平和安装在姿态调整机构上的支杆组成的多自由度弹簧-质量块弹性系统,通常情况下支杆长度是模型长度的三到五倍。而模型在进行风洞实验时会受到风洞气流脉动的影响。风洞气流脉动包括三种形态:压力脉动、速度脉动(俗称湍流度)以及温度脉动、速度脉动(俗称湍流度)以及温度脉动。模型受力情况如图1所示。
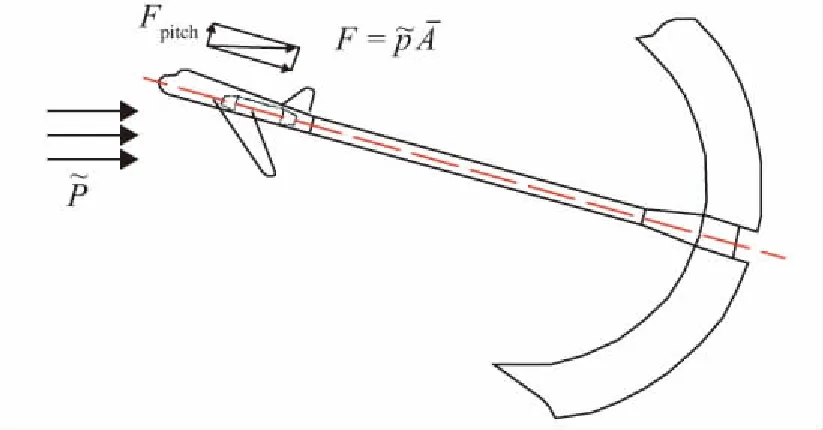
图1 模型受力情况
模型在进行跨声速风洞实验时压力脉动为主要形态,压力脉动会对模型系统造成高频、低频两类扰动,而这种低频扰动与模型系统低阶固有频率相耦合,导致模型及支杆产生振动,尤其在模型实验攻角增大时,振动明显加剧[6-7]。
压电陶瓷本质上是电容,在一定电压作用下,陶瓷晶体会膨胀,如果陶瓷在伸长方向受到机械约束,那么陶瓷将会给机械结构施加一个反力。而且压电陶瓷作为作动器,输出力的频响可以达到数千赫兹。目前,以德国PI公司生产的一款压电陶瓷为例,一个未封装的25×60 mm压电陶瓷最大可输出15000 N的力。
抑振原理分析图如图2所示。模型在向上振动时,上半平面的压电陶瓷组通电工作,由于支杆空间结构的约束,压电陶瓷组输出很大的轴向力,产生一个与模型端俯仰弯矩相反的平衡力矩,其大小取决于压电陶瓷两端电压以及陶瓷在截面的安装位置,从而达到抑制振动的效果。
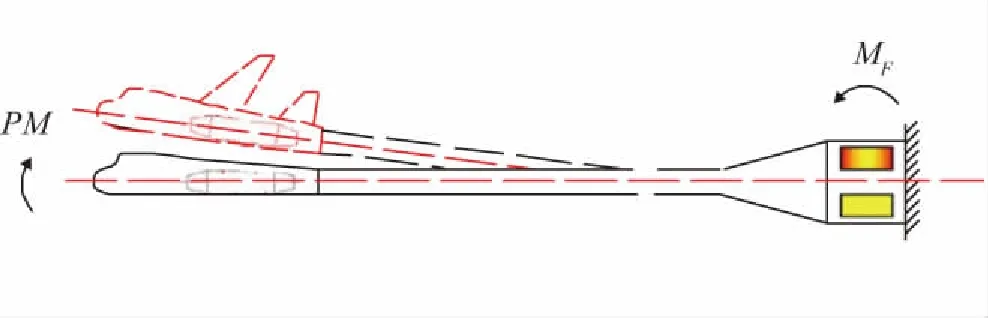
图2 抑振原理分析
2 支杆结构设计
2.1 周向分布
由于支杆与压电陶瓷空间尺寸的限制,采用4个压电陶瓷环形均布的排列方式,安装方式主要有如图3所示的两种,其中,y轴表示俯仰方向,z轴表示偏航方向,鉴于模型振动主要发生在俯仰方向,布局2中左右2支陶瓷对于俯仰方向的振动抑制不产生作用[8]。同时,相比于布局2,布局1在俯仰方向刚度更高,所以压电陶瓷周向布局选用第一种方式,上下各2支,正交对称安装。
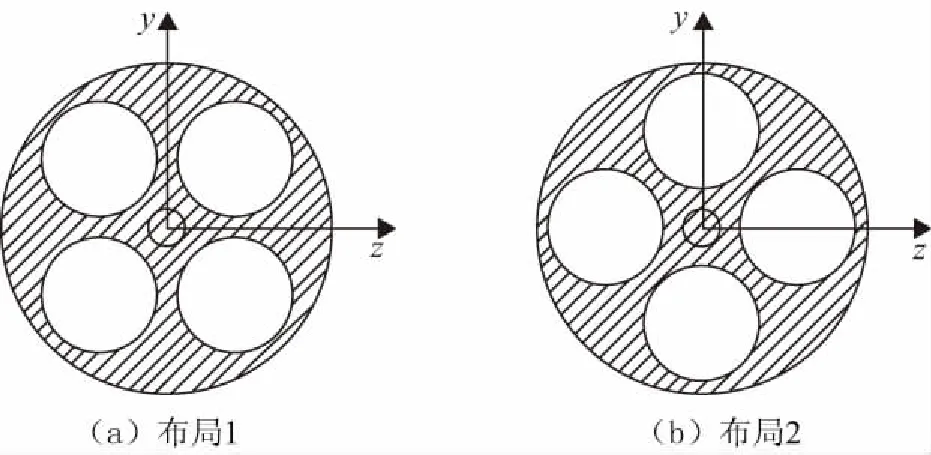
图3 作动器布局方式
2.2 轴向距离
主动抑振器的设计思路为驱动叠堆式压电陶瓷作动器输出的力和位移,使支杆产生反向的弯曲,消减气动脉动载荷在支杆上产生的挠度,利用作动器的高频响配合实时控制系统即可实现模型振动的抑制。而压电陶瓷的安装位置对作动器输出能力的表现有很大影响。
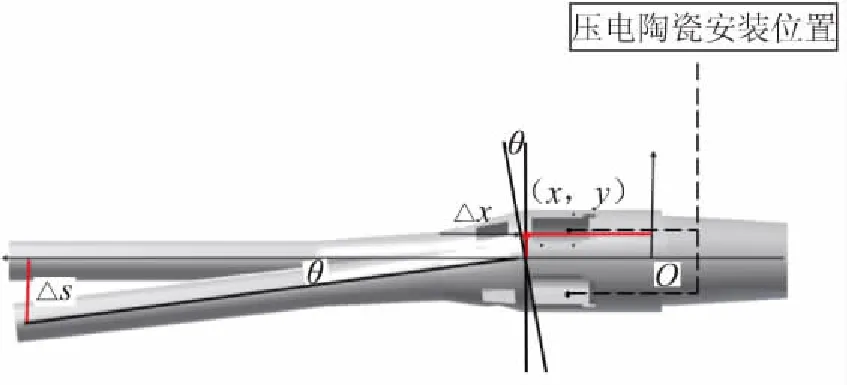
图4 轴向安装位置
压电作动器在电压驱动下,力和位移输出关系
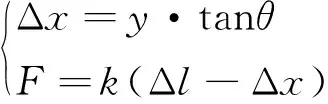
(1)
压电作动器驱动力产生的力矩
M=F·y=k(Δl-Δx)·y
(2)
为保证安全性,参考原始支杆结构数据,所设计的支杆截面惯性矩在相同位置处不小于原支杆
(3)
D≥73.6 mm
(4)
确定可安装作动器位置区间为x∈[53,140.47]mm。代入压电作动器性能参数,支杆结构、材料力学参数[9],在区间内寻找静态位移输出极值点
市民的满足需要性预期以及城市建设的可靠性预期是智慧城市预期的两个重要方面。引导市民建立适当的期望值以及加强智慧城市建设的可靠性,可以更好地为市民提供智慧化的服务,降低智慧城市市民抱怨程度。因此,我们假设:
(5)
图5所示曲面表现出作动器输出特性、安装位置与输出能力三者之间的关系,在压电陶瓷选择完毕参数确认的情况下,得出x局部最优解为140 mm,即压电陶瓷作用面距离支杆固定端距离为140 mm。
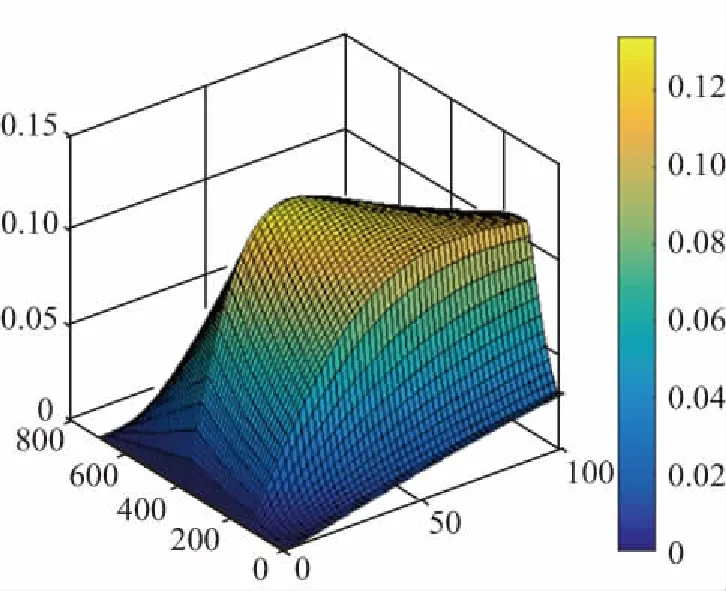
图5 位置—静态输出位移分布二维曲面
2.3 静强度校核
飞行器在进行大攻角实验时,模型受到的静载荷往往达到4000 N以上,而本文所设计的振动抑制系统是针对国内某高速风洞,表1所示数据为该风洞某模型在0.85 Ma风速下的升力情况。
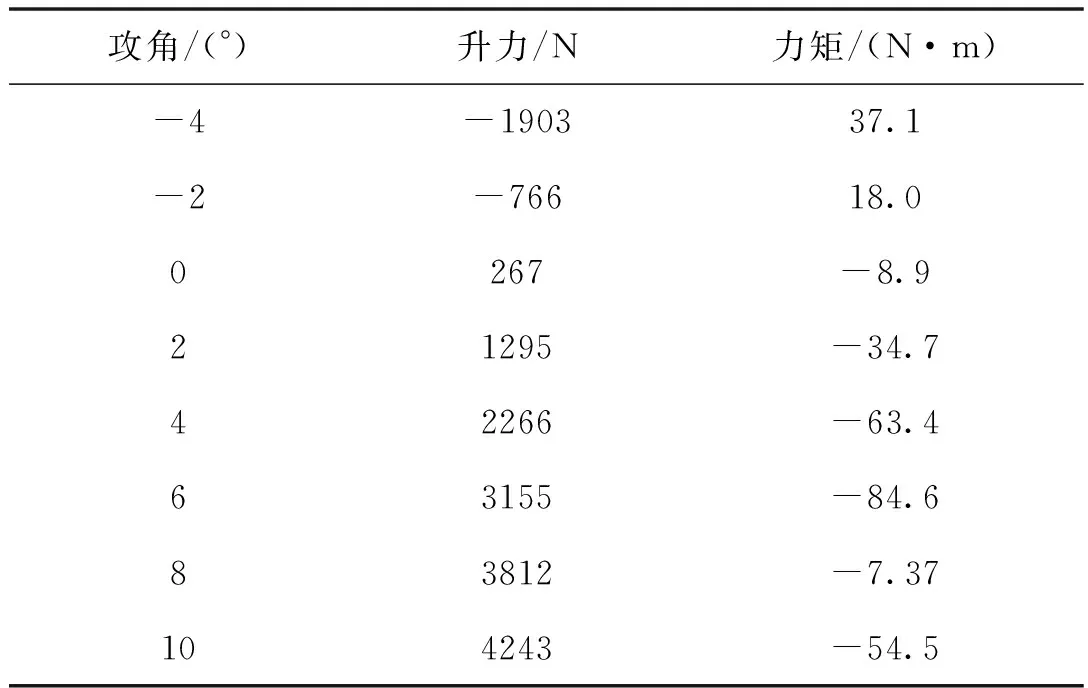
表1 不同攻角下模型受力情况
由表1可知,该模型在实验攻角为10°时,模型俯仰方向所受的升力达到4243 N,同时还存在-54.5 N·m的弯矩,因此本文针对此极端工况下的支杆进行了静强度校核。支杆应力及自由端位移变化如图6 所示。
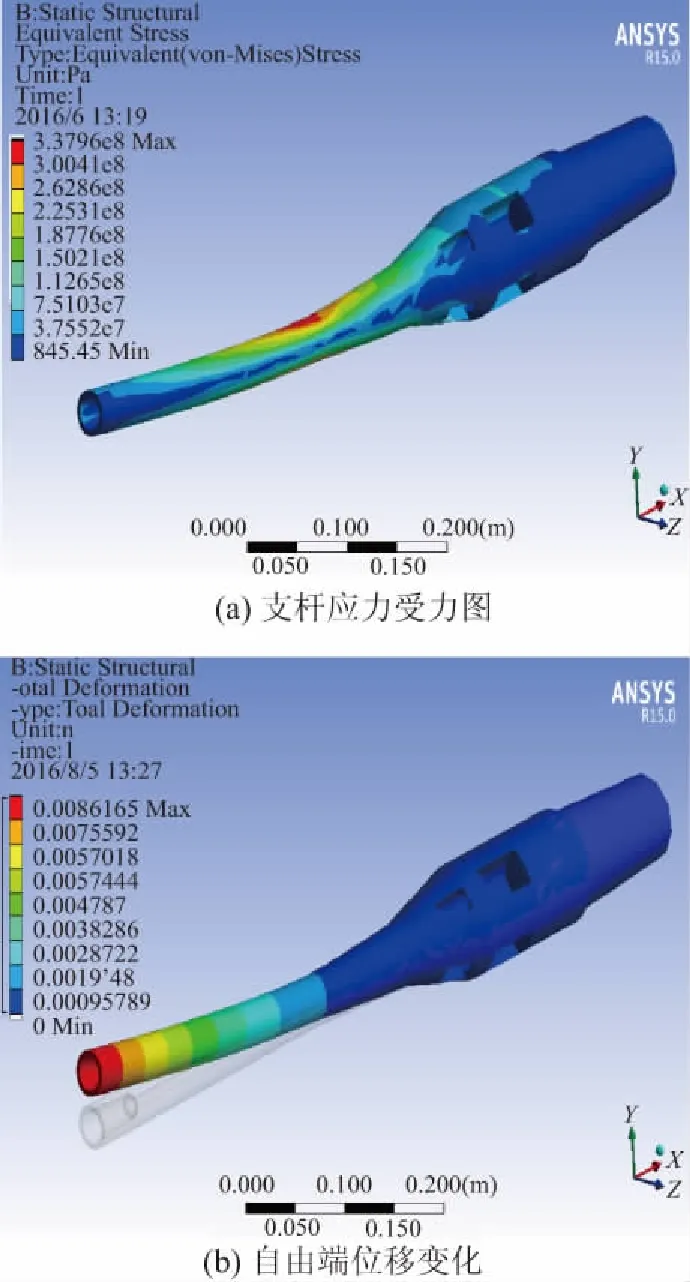
图6 支杆应力及自由端位移变化
将模型导入ANSYS有限元分析程序,固定支杆与弯刀机构的连接面,在模型自由端Y方向施加4243 N的静态力,在Z方向施加-54.5 N·m的静态弯矩。分析结果显示,在支杆靠近中间位置,支杆最大等效应力达到338 MPa,自由端模型最大位移为8.61 mm。本文设计的支杆材料选用风洞实验中常用的F141(18Ni-200),材料屈服强度1800 MPa,安全系数大于5.3,所以本文所设计的支杆满足极端载荷下的静强度要求。
2.4 模态分析
结构的振动特性决定了结构对各种动力载荷的响应情况,所以在进行动力学分析前先进行模态分析。
假定系统为自由振动并忽略阻尼,其方程为
[M]{ü}+[K]{u}={0}
(6)
当发生谐振动时,即u=Usin(ωt)时,方程为
(7)
结构固有频率ωi及振型fi都可从上式中得到。本文采用有限元软件对“模型-天平-支杆”系统进行模态分析,模型与天平之间、天平与支杆均采用锥面配合,虽然模型与天平是用螺纹紧固,天平与支杆用键紧固,但是在风洞实验条件下,风洞实际载荷均由锥面承担,所以螺纹连接面选用切向和法向均无法分离的“Bonded”方式连接。而天平与模型及支杆之间的锥面连接,选用“No Separation”接触,在载荷较大的情况下,允许接触面发生少量的无摩擦切向滑动[10-11]。杆模型模态分析如图7所示。

图7 杆模型模态分析
在风洞流场环境中,模型系统与风载激励耦合,主要是在俯仰方向产生剧烈共振,因此本文也是针对模型系统俯仰方向的振动进行抑振实验, 表2为支杆前六阶固有频率数据,可知模型在俯仰方向,即二阶固有频率为16.431 Hz,这与原支杆俯仰方向固有频率15.6 Hz,相差不多。
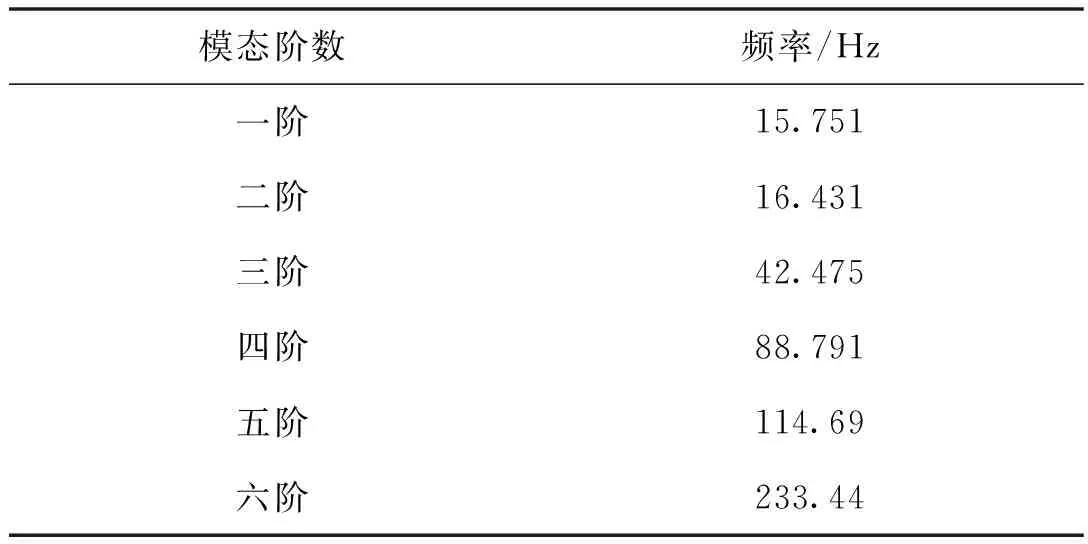
表2 支杆前六阶固有频率
2.5 谐响应分析
2.3节进行了支杆的静强度校核,由于风洞中支杆受风载激励,在俯仰方向产生低频大幅共振,所以在进行静强度校核的情况下,同时还要分析支杆振动时应力状态。在模型端施加F=100 sin(2pft)动态激励载荷,幅值100 N,f取俯仰方向固有频率16.5 Hz。分析结果如图8所示。
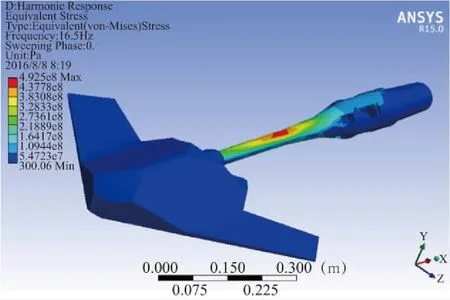
图8 谐响应分析
从图8在支杆靠近中间位置,支杆最大等效应力达到492 MPa,也远小于材料的屈服强度。所以,本文设计的抑振器支杆满足风洞实验的强度安全要求。
2.6 压电作动器安装与预紧
由于本文选用的堆叠式压电陶瓷只能承受轴向载荷,较大的剪力会破坏压电陶瓷原有的结构。为了避免陶瓷在安装及输出过程中受到较大剪力的破坏,随即在陶瓷顶端设计了一个接触球面,将其用环氧树脂粘连在压电陶瓷顶部,轴向采用紧定螺钉进行预紧,螺钉直接作用球面,使得陶瓷在使用过程中不受剪力影响。为了避免陶瓷安装部分复杂的表面形状造成抑振器周边流场混乱,在四个陶瓷周围加上一层弧形盖板,保持整体抑振器的气动外形与支杆外圆一致,如图9所示。

图9 作动器安装结构
3 实验室分析
3.1 实验室抑振系统搭建
根据上一章设计的风洞实验支杆,搭建了一套实验室抑振系统。如图10所示,刚性支座固定于大理石实验平台,将装有两组压电陶瓷的风洞实验支杆安装在刚性支座上,并用斜键拉紧。天平安装于支杆前端,并深入飞行器模型内部,与模型固连。由于本文中的高速风洞实际载荷较大,所以选用峰值载荷为500 N的大功率激振器模拟风洞实际载荷。

图10 实验室抑振系统
在此实验基础上,本文选用dSPACE实时控制系统完成实时控制。由于实际风洞实验环境条件复杂恶劣,常规的位移及速度传感器难以完成模型振动的实时测量及反馈,所以将体积小、响应快的加速度计粘贴在模型内部,作为振动测量的传感器。抑振系统总体框图如图11所示。
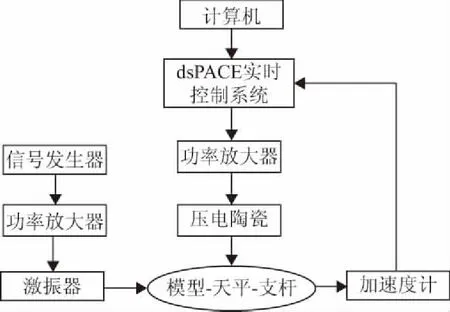
图11 抑振系统总体框图
按照上述控制原理,控制系统硬件由计算机、dSAPCE及功率放大器组成。控制程序包含输入/输出端的模数/数模转换、低通滤波、控制律及限幅环节(防止工作电压超出压电陶瓷安全工作电压)。目前,振动主动控制算法主要有 PID 控制算法、二次型线性最优控制算法、模糊控制算法等。依据风洞实际需要,控制算法需要在很快的时间内完成振动抑制,控制信号的输出存在一定的滞后,且风洞内工况复杂,所以本文选用鲁棒性和可靠性较强的PD控制。
对于PD控制器,其理想的传递函数为
G(s)=Kp+Kds
(8)
式中:Kp为比例常数,Kd为微分常数实验中通过对两参数进行合理整定,可以提升抑振器在不同工况下的抑振性能。
3.2 实验结果分析
本文探究了两种振动状态下的主动抑振器的振动抑制效果,第一种是通过锤击获得自由振动状态下的抑振效果,第二种是支杆系统在激振器输出的正弦激励下,受俯仰方向的共振时的振动抑制。
通过多次锤击实验,控制参数整定为Kp=50,Kd=0.2时,未打开控制器和经控制器抑振后,支杆振动衰减结果如图12所示。未开启控制器,支杆振幅在30 s后衰减到零,而打开抑振器以后,仅用时2.2 s,支杆振幅就衰减到零。从图12中可以明显地看出,本文设计的抑振器可以很好的抑制俯仰方向的自由振动。
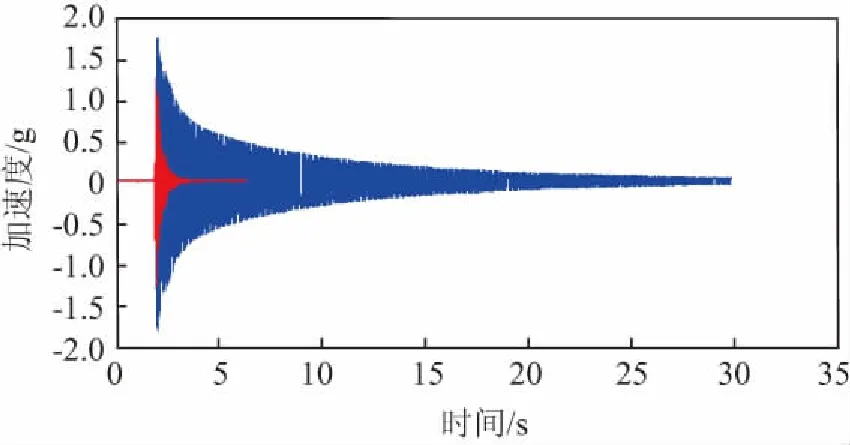
图12 锤击实验结果
在不改变其他实验条件的情况下,激振方式由锤击改为激振器正弦激励。同时,可以通过调节激振器的输出增益,进行不同振动强度下的振动主动控制实验,获取不同振动强度下的振动抑制结果。
在调节激振器输出的情况下,分别进行了峰值加速度为0.5 g,1.3 g,2 g的振动主动抑制实验,实验结果如表3所示。
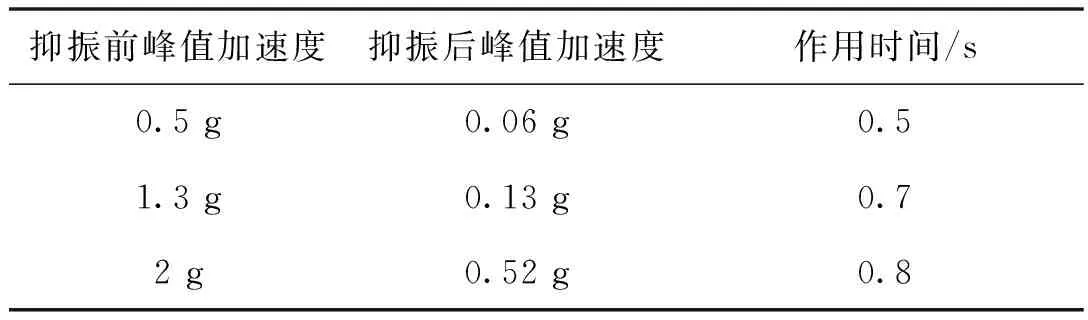
表3 抑振结果
通过调节PD控制参数,在P=200,D=0.2时,获得最佳抑振效果,如图13所示。
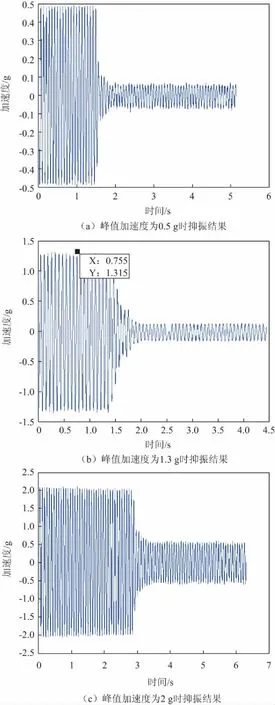
图13 激振器激励抑振结果
从表3可以得出,三组实验结果剩余振幅比分别为12%,10%,26%,对支杆自由端的振动有明显地减弱。本文所设计的抑振机构,可以很好的抑制由外激励作用而产生的支杆大幅振动。
4 结论
本文针对尾撑式支杆系统在进行跨声速风洞实验时产生的振动问题,在原有支杆的基础上重新设计了支杆结构,并以此为基础,设计了一套基于压电陶瓷作动器的内嵌结构主动抑振系统,构建了基于PD调节器的实时控制系统,实现了对支杆俯仰方向振动的抑制。在实验室条件下,进行了峰值加速度为0.5 g,1.3 g,2 g的激振实验,在抑振器开启的情况下,分别用时0.5,0.7,0.8 s将振幅抑制到30%以下。
