柔性关节机器人动力学分析

王鸿熠 韩先国

（北京航空航天大学 机械工程及自动化学院，北京 100191）

自诞生至今，工业机器人在工业领域得到了越来越多的应用[1]。近年来，除了在传统的焊接、喷涂等领域的应用外，工业机器人以其机动、灵巧等特点，开始越来越多地应用于航空航天领域[2-3]。但串联机器人刚度较差，使得其应用受到了一定的限制。

机器人动力学是对机器人刚度分析及振动分析的重要基础。本文以ABB IRB4600机器人为对象，建立了考虑关节柔性的动力学模型，并给定了机器人运动轨迹，分析了机器人运动过程中的关节变形情况。

1 关节柔性模型简化

1.1 机器人柔性来源分析

串联型工业机器人的柔性主要体现在两个方面，即连杆柔性和关节柔性[4]。连杆柔性表现为机器人各杆在力的作用下发生变形。关节柔性表现为各个关节在力的作用下发生形变。通常，机械臂各连杆刚度大于关节刚度，机器人连杆变形可以忽略，现仅考虑机器人关节柔性造成的影响[5]。

关节柔性造成的影响主要有两点。一是在机器人运动过程中，机器人各关节受到驱动力作用，产生关节变形，该形变影响了机器人的绝对定位精度。二是机器人的振动，其主要体现在两个方面：当机器人运动结束后，各关节的变形依然存在，随着运动过程中积累的能量释放，系统出现残余振动；机器人在某一位姿下，受到变化的外部力作用，各关节变形也随之改变，导致系统振动。本文重点分析机器人运动过程中及运动结束后机器人关节角度及末端振动情况。

1.2 关节柔性模型简化

spong在1987年首先提出了柔性关节简化模型。该简化模型对于实际关节有如下假设：机器人关节在关节力作用下只存在微小变形，该变形处于线弹性范围内，机器人各关节可视作线性扭簧；电机转子轴线与关节轴线同轴，可将电机转子视为质量均匀的轴对称刚体；将电机视为理想力矩源，与机械动力学相比，电机电气动力学足够快，可以忽略其动力学影响。

根据以上假设，可以将机器人关节简化为一线性扭簧（扭簧刚度为k）。

2 机器人运动学分析

2.1 机器人坐标系建立

机器人坐标系建立是机器人运动学分析及动力学分析的前提。采用前置D-H参数法，建立IRB4600关节型机器人连杆坐标系，如图1所示。

图1 机器人连杆坐标系示意图

2.2 机器人正向运动学

机器人相邻两杆间的位姿变化矩阵可以表示为i可以得到机器人末端相对于机器人基坐标系的齐次变换矩阵为：

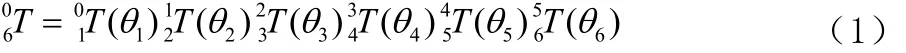
3 关节柔性机器人模型

3.1 柔性关节机器人动力学

拉格朗日法推导机器人系统动力学方程的步骤可以概括为：（1）选取机器人关节坐标系、电机转子转角坐标系为广义坐标；（2）求解系统动能表达式，包括连杆动能与电机钻子动能；（3）求解连杆与电机转子势能；（4）构造拉格朗日函数并推导动力学方程。

关节柔性的机器人连杆系统动力学方程可以表示为：

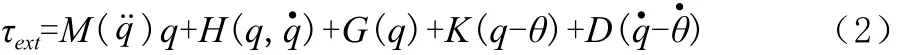
式中：τext为外力作用下关节力矩；M(q)为质量矩阵；H(q,q˙)为非线性科氏力和离心力矢量；G(q)为重力项；K=diag(k1,k2,k3,k4,k5,k6)为关节刚度矩阵；D=diag(d1,d2,d3,d4,d5,d6)为关节阻尼矩阵。

3.2 关节柔性机器人运动仿真

3.2.1 关节空间的轨迹规划

在关节空间内采用三次多项式进行轨迹规划。对于关节i，驱动机构输出转角θi可表示为时间的函数，设其三次多项式参数为ai0、ai1、ai2、ai3，即：

给定机器人各关节首末角度及运动时间，即可确定机器人电机输出转角、角速度随时间的变化规律。表1为机器人关节转角变化情况，设定运动时间为2.5s。机器人在运动首末端点的速度值均为0，得到三次多项式各项系数。

表2 运动仿真起始值与终止值

3.2.2 Simulink运动仿真分析

在机器人运动过程，机器人末端所受广义外力为0，可将式（2）改写为：

需要注意的是，式（4）中各项的刚度不同，在数值分析中，该种形式的微分方程被称为刚性方程，又被称为病态方程。病态方程的求解相较于通常的微分方程更为困难，MATLAB中的simulink仿真模块包含多种求解方法，其中的ODE15s求解方法属于一种多步预测算法，适合求解大刚度系统的微分方程。

在simulink中搭建仿真模型，可以得出机器人运动过程中及运动结束后，机器人各关节的变形情况及关节角度随时间的变化情况，通过式（1）即可得到机器人末端位置在机器人基坐标系中X、Y、Z三个轴方向的误差值，如图2所示。

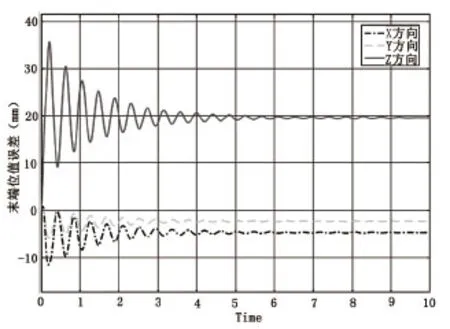
图2 机器人末端振动随时间的变化规律

分析图2可得，在机器人运动过程中，由于关节柔性的存在，机器人末端位置与理论位置之间存在误差，该误差随着运动时间的延续表现为末端振动情况。在运动结束后，机器人末端位置与理论位置并不重合，这是由于重力因素造成的。

4 结论

本文采用D-H参数建立了机器人连杆坐标系，求得了机器人运动学模型。采用拉格朗日法建立了考虑关节柔性的机器人动力学模型。在制定机器人各关节运动首末关节角度值和运动时间后，对机器人的运动轨迹在关节坐标系内进行了三次多项式运动规划。建立了simulink仿真模型，得出了机器人各关节角度在指定运动情况下的关节变形情况，并分析了机器人末端振动情况，这对于工业机器人动力学相关研究有一定的借鉴意义。