基于非线性拟合的高压电机功率因数补偿
2018-08-15梁伟平牛博通
梁伟平,牛博通
(华北电力大学 自动化系,河北 保定 071003)
0 引言
据统计,2015年我国全社会用电量为5.55万亿kW·h,电机总耗电量约3.5万亿kW·h,占全社会总用电量的65%,其中三相异步电动机耗电量占电机耗电总量的70%[1-2]。异步电动机为感性设备,运行过程中会消耗无功功率,导致其功率因数降低。若由电网系统供给提供无功功率,会使总供电电流增大、限制有功功率的输出、增加线路和设备的铜损,进而增加电能的损耗。高压(6 kV~10 kV)电动机的用电量占工业用电的一半以上,其额定功率很大,设计时会留出一定的裕量。高压电机在非额定功率下运行进一步降低了其功率因数。根据国家对电力系统功率因数要求以及节能减排的趋势,对电机系统进行功率因数补偿意义重大:改善电压质量与电动机运行状态,提高功率因数;减轻电气开关和供电线路负荷,减少电费支出率;提高系统安全性。
在众多无功功率因数补偿的方式中,就地无功补偿是最经济简单的一种方式。就地直接进行补偿能够改善配网末端的电压、提高电机工作效率,具有投资少、配置方便等特点,因而得到了广泛的应用。
1 补偿原理
异步电动机运行时是感性负载,电动机电流滞后于电源电压,这一感性阻抗特性使得它们运行过程中需要消耗无功功率。三相异步电动机T型等效电路如图1所示[3]。
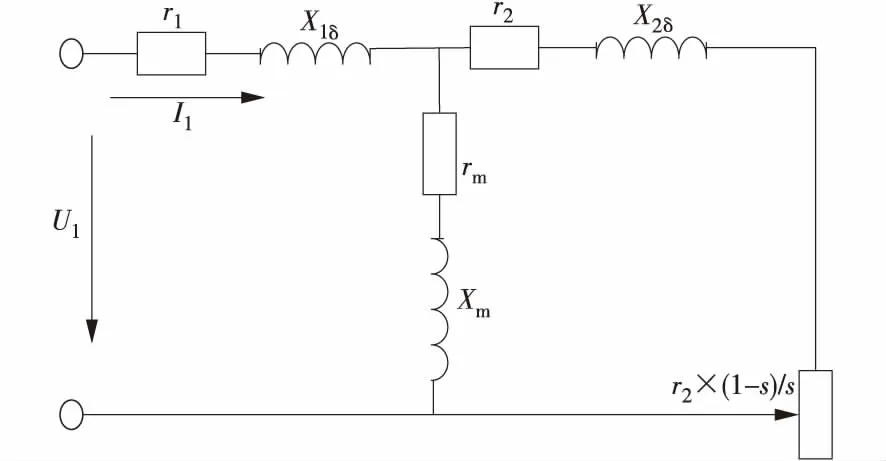
图1 三相异步电动机T型等效电路
图中:r1为定子电阻,Ω;X1δ为定子电抗,H;rm为励磁电阻,Ω;Xm为励磁电抗,H;r2为转子电阻折算值,Ω;X2δ为转子电抗折算值,H;r2×(1-s)/s为虚拟电阻,Ω;U1为无穷大电网电压有效值,kV;I1为定子电流,A。
加入就地无功补偿相当于将电容器并联,线路电流下降,相应的有功功率和无功功率如图2所示[4]。
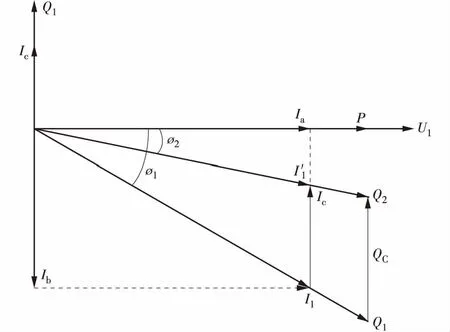
图2 补偿前后电流和功率变化
根据补偿的容量不同可分为两种情况:若补偿后电流仍滞后于电压,为欠补偿;若电容容量较大,电流超前于电压,便称为过补偿。补偿后的功率因数
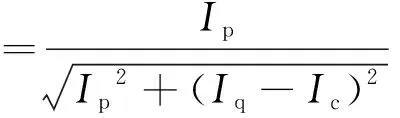
(1)
式中:Ip为有功电流,A;Iq为无功电流,A;Ic为补偿电容电流,A;cosø为功率因数。
根据补偿前后有功电流不变得
I1cosø1=I2cosø2=Ip,
(2)
式中:I1为补偿前线路的电流,A;U1为补偿前线路的电压降,kV;ø1补偿前线路的功率因数角;I2为补偿后线路的电流,A;U2为补偿后线路的电压降,kV;ø2补偿后线路的功率因数角。
根据欧姆定律
(3)
式中:r为线路单位长度电阻,Ω/km;L为线路长度,km。
由于补偿后的功率因数得到提高,所以式(3)中的U2小于图1中的U1。加入无功补偿可以改善线路电压、提高功率因数,无论对经济性还是安全性都发挥了积极的作用[5]。
2 补偿容量计算与分析
三相异步电动机的定子接入三相供电电源后会产生旋转磁场,我们称之为主磁场。这部分磁场就会产生相应的无功功率,而这部分无功随负荷从零到满载时的变化不大。与主磁场相对应的还有漏磁场,这一部分磁场是由经过气隙而非经过转子的一部分磁通和由转子电流产生的只经过转子的一部分磁通产生。空载时,定子电流基本上用来产生主磁通,功率因数很低;随着负载电流增大,输入电流中的有功分量也增大,功率因数逐渐升高。所以在不同的负载率下,将功率因数补偿到相同值需要的无功容量不同。以额定功率为1 250 kW的水泵为例,在不同负载率下其补偿容量见表1[6]:其中I为定子电流,A;P为有功功率,kW;cosφ为功率因数;Q为当功率因数为0.92时需要补偿的无功容量。
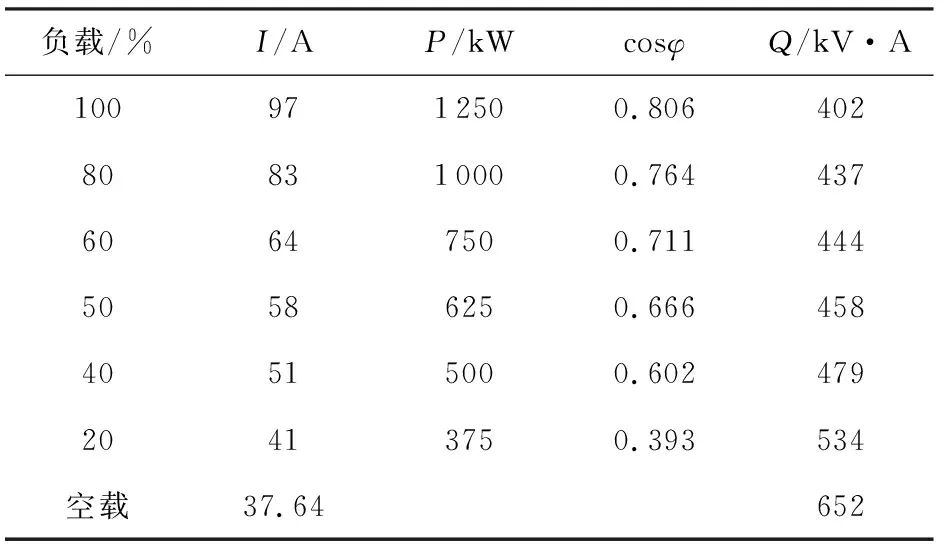
表1 负载与补偿容量的关系
鉴于目前高压电动机庞大的数量,若不能在其负载发生变化时准确计算补偿容量,将会对电网的稳定和电压的质量产生严重干扰和影响,同时也难以满足节能减排的要求。常用的补偿容量的计算方法有如下3种。
2.1 实测有功功率和功率因数法
利用电能测试仪或者利用电度表以及平均功率得到电动机的实际功率Ps和功率因数cosøs;然后假设补偿后想要提高到的功率因数为cosøe。则补偿的容量计算公式为
Q=Ps(tanøs-tanøe) ,
(4)
式中:Q为无功补偿容量,kV·A。该公式中的实际功率Ps为实际测量所得,得到的容量非常准确;但是若为简化使用额定功率代替Ps,就会造成容量的不准确。
2.2 基于实测线电流算补偿容量
当无法测得实测功率时,可以利用实测的电流值得到负载率,近似计算实际功率近似为
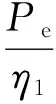
(5)
式中:β为实际负载率;η1为对应负载率下的电机效率;Ps为计算得到的近似实际功率,kW;Pe为额定功率,kW。
负载率的计算公式根据机端电压可以分为两种:额定电压下的负载率,如式(6);非额定电压的负载率,如式(7)所示。
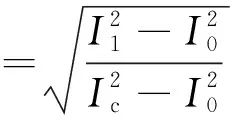
(6)
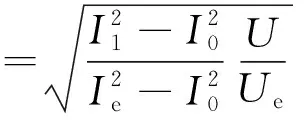
(7)
式中:Ie为电动机的额定电流,A;I1为实际电流,A;I0为空载电流,A。将根据式(6)或(7)得到的β,代入式(5)得到Ps,再将Ps代入式(4),可得到补偿容量。
2.3 基于空载电流法
利用空载电流法计算高压电机的补偿容量时,考虑到高压电动机容量大,当电动机的电源被切断后,电动机会因为惯性保持一段时间的转动,这时将其看作一个发电机;加之高压电机无功补偿的容量大,电容中的这部分无功功率就会产生放电电流,产生较大的励磁电压,对电容器造成很大的损害。计算中经常会按照0.9倍的空载电流,来计算补偿容量,以防止在电机切开时产生过电压,计算公式为[7]
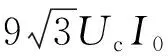
(8)
式中:I0为空载电流,A;Uc为额定电压,kV;Qc为补偿容量,kV·A,其中I0计算公式为
I0=2Ic(1-cosøc) ,
(9)
式中:Ic为电动机的额定电流,A;cosø为电动机的额定功率因数,额定电流计算分式为
(10)
式中:ηe为额定效率,Pe为额定功率。
空载电流也可以根据最大转矩系数来计算,
(11)
其中:Ie为电动机的额定电流,A;b为转矩系数;øe为额定功角,(°)。
2.4 容量计算分析
在实际的功率因数补偿中,按照计算加入一定裕量后的补偿容量,仍然不能得到理想的功率因数。一方面是因为电机制造厂给出的额定参数不够准确。另一方面是因为补偿装置的额定容量不是实际输出的容量,这是因为装置为抑制电容器投入时的浪涌电流,经常串联小比例的电抗器。如果串联的电抗器在电容器中的电抗率小于1%,对电容器实际容量的影响可以忽略不计,而当电抗率超过了1%之后,就必须考虑电抗器造成的实际容量减小问题。本文假设电抗率为6%,计算容量时将电抗率考虑在内。
3 异步电机无功补偿Matlab仿真
3.1 仿真电机参数
采用某电厂的6 kV段一次风机作为仿真的异步电机,型号为YKK710-4。该电机为鼠笼型;额定电压,6 kV;额定电流,205.4 A;额定有功功率,1 800 kW;额定转速,1 495 r/min;额定效率,95.8%;额定功率因数,0.88;启动转矩倍数,2.1;额定转矩,11 500 Nm;定子电阻,2.38;定子漏感,0.74 mH;转子电阻,2.26;转子漏感,0.76 mH;激磁电感,70.03 mH;转动惯量,900 kg·m2。
3.2 仿真模型
模型的主要模块包括三相电压源模块、发电机模块、三相负载模块以及计算功率因数的模块和自动计算补偿容量的模块。
3.3 仿真分析
根据给定的高压一次风机的额定参数,基于0.9倍的空载电流计算补偿容量的方法,根据式(8)~(10)得到应补偿的容量为461 188 kV·A。考虑实际补偿电容器中有6%的电抗率,则实际的补偿无功为433 517 kV·A。仿真三相电源模块设置额定电压为6 000 V,频率为50 Hz,并联的负载按照计算值设置容量,仿真时间选为80秒,将电动机负载率从100%降到空载,得到的有功、无功变化如图3所示。
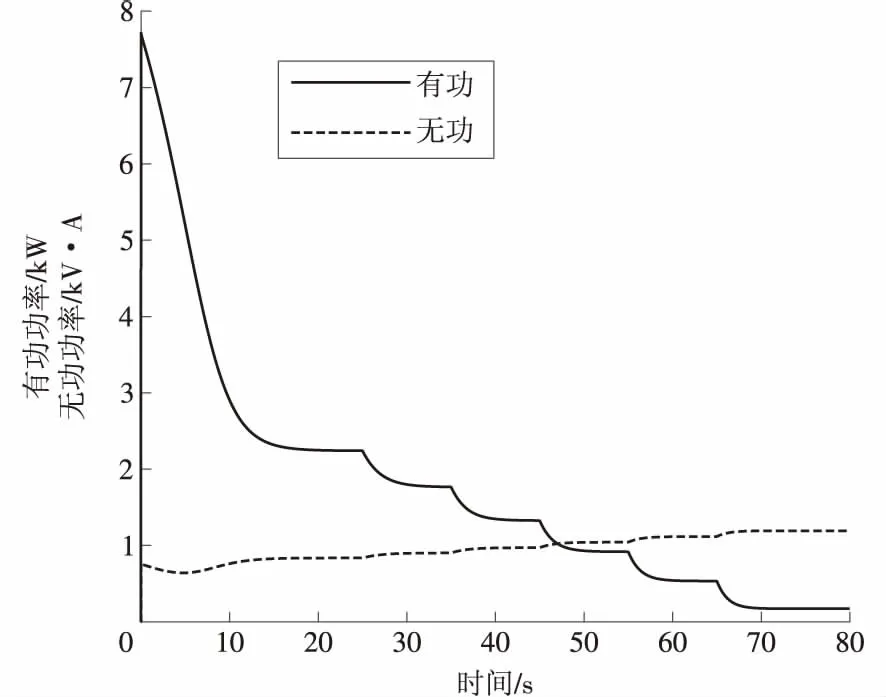
图3 按公式计算补偿后发电机在不同负载下的有功和无功功率
根据结果,采用基于0.9倍的空载电流计算补偿容量的方法计算就地补偿容量的功率因数仿真结果见表2。
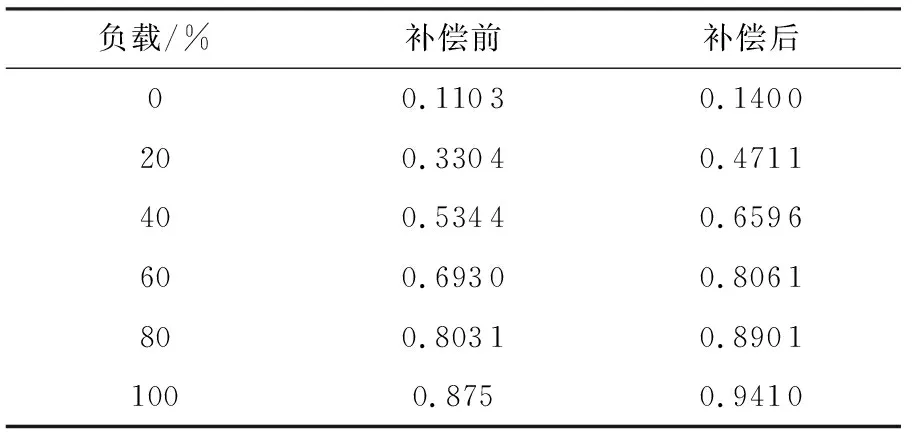
表2 不同负载率下补偿前后功率因数
根据仿真结果明显发现,只有高压一次风机在较高的负载时,适合采用基于0.9倍的空载电流计算补偿容量的方法,其补偿后的功率因数可以达到0.94。在其他工况下,尤其在低负荷的时候,功率因数严重偏低,补偿效果非常差。
4 参数拟合
4.1 补偿容量的非线性拟合
根据仿真结果分析,高压电机在不同的负载率下对于补偿的容量需求不同。采取固定容量补偿,高压电机的功率因数在低负荷的时候就会很低。这既会影响电能质量、造成电能损耗,又增加电费支出,易危害电动机等设备。所以容量应该随着不同的负载率变化。我们对模型在以上负载率是达到0.94的功率因数时的补偿容量进行仿真,得到的数据见表3。

表3 不同负载率下最优补偿容量和定子电流
对不同负载下的最优功率进行分析,利用Matlab提供的曲线拟合工具箱进行拟合。采用多项式拟合,找到一条二阶的曲线能够基本与补偿的无功功率容量拟合曲线相重合,该曲线的公式为
y=-0.023 3x2-10.243x+1 727.1 ,
(12)
式中:x为负载率,%,y为应补偿的无功功率,kV·A。
拟合曲线如图4所示。
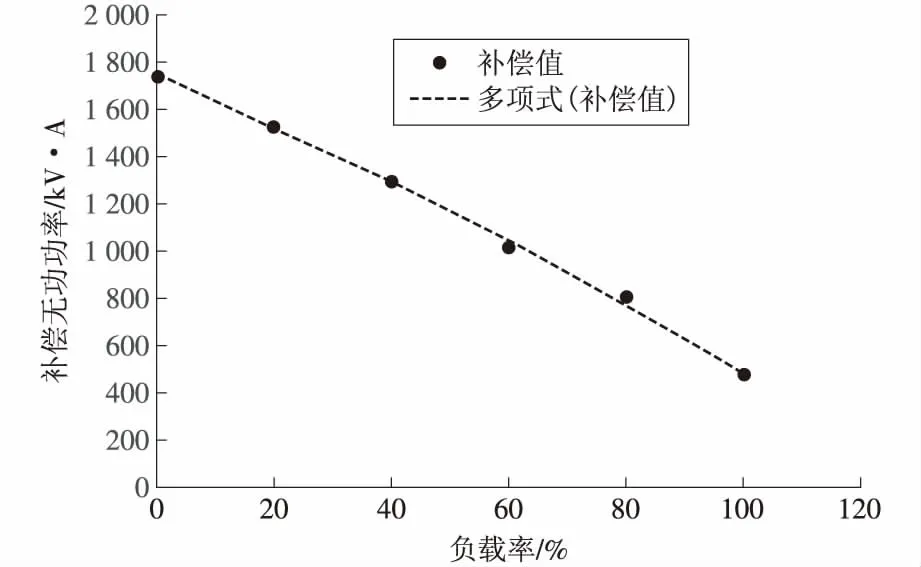
图4 不同负载下的最优功率拟合曲线
拟合曲线基本覆盖所有点,曲线的方差(SSE)为0.021 16,确定系数(R2)为0.998 10,标准差(RMSE)为0.026 56。利用代表最优曲线的结果进行仿真,在负载率为30%、50%、70%和90%时得到的按最优曲线补偿的功率因数,将其与基于0.9倍空载电流计算补偿容量的方法进行比较,结果见表4。
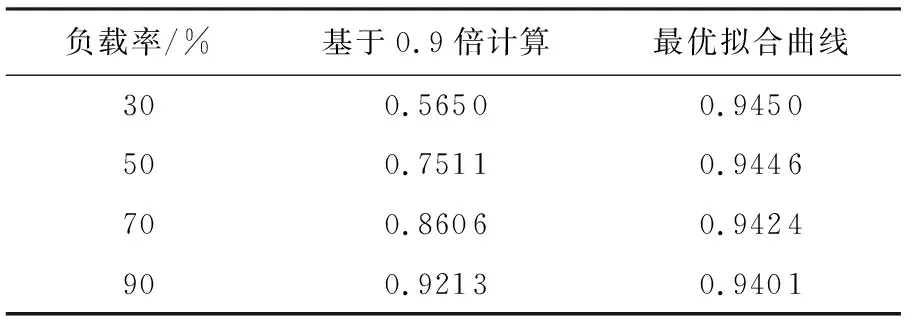
表4 最优曲线法与空载电流补偿法功率因数比较
4.2 负载率拟合
根据最优拟合曲线计算时,需要有实时的电动机负载率,而负载率和定子电流关系密切,根据仿真得到的在不同负荷率下的定子电流,同样利用曲线拟合的方法,可以将定子的电流数据拟合为一条曲线,拟合公式
y=-0.000 399 6x2+0.567 7x-0.019 15 ,
(13)
式中:x为定子电流,A,y为负载率,%。
拟合曲线如图5所示。曲线的方差(SSE)为0.002 60,确定系数(R2)为1,标准差(RMSE)为0.029 46,可以近似代表定子电流曲线。
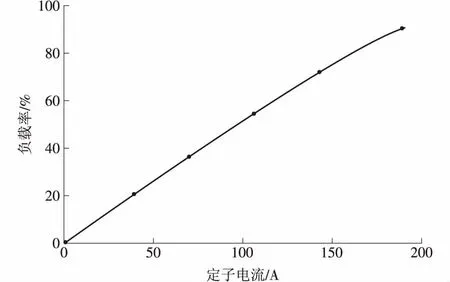
图5 定子电流对应负载率拟合曲线
利用最优无功补偿容量拟合曲线和定子电流拟合曲线(如图6和图7所示),在35%和75%两个负载率下进行仿真。仿真结果显示,当负载为35%和75%时的额定电流分别为64.67 A、147.4 A;根据式
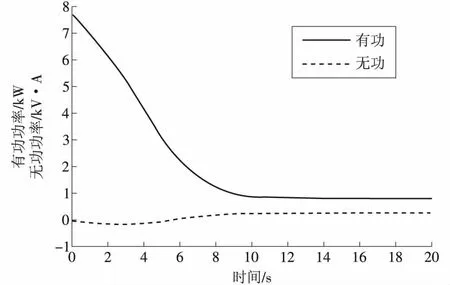
图6 负载率为35%时利用拟合曲线补偿结果
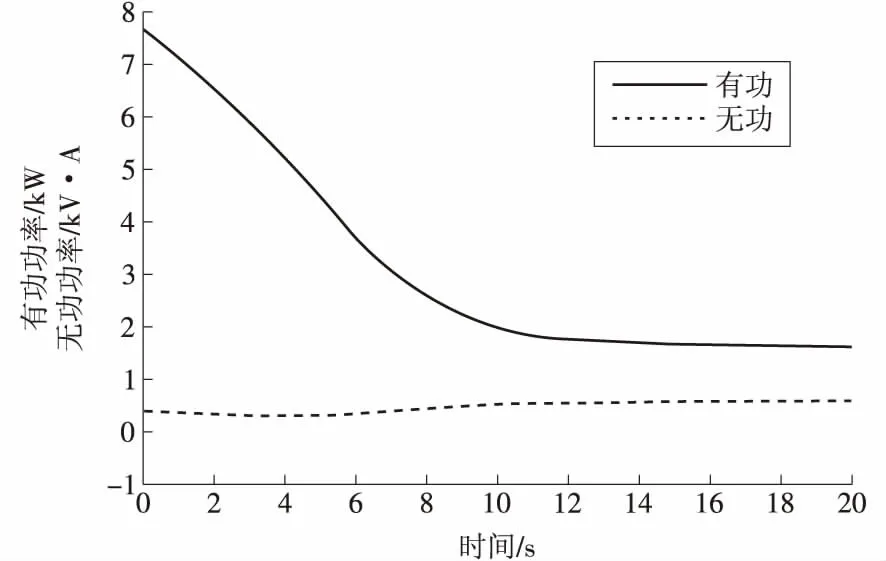
图7 负载率为75%时利用拟合曲线补偿结果
(13)得到对应的负载率为35.022 8%和74.997 8%,可以比较准确的预测负载率情况;再根据(12)式,得到此时应补偿的容量,利用得到的仿真容量对电流为64.67 A,147.4 A;在两个工况下进行Matlab仿真,仿真时间为20 s,其功率因数分别为0.945 7和0.941 8。
5 结论
高压异步电动机就地无功补偿容量计算受负载情况影响严重,常用的无功补偿容量计算方法难以在非额定负载下实现功率因数补偿,利用最优数据进行补偿功率曲线拟合是一种值得推荐的实现特定电动机补偿的方法。根据电机最优补偿容量数据呈现的非线性特点,只需要少量工况点就可以实现最优拟合。另外通对大量多类型电机最优曲线分析,根据电机额定参数找到一种对曲线参数进行修改的统计规律,实现拟合曲线的普适性是未来研究的一个重要方向。
