数学期望在工业企业经济决策中的应用研究

刘昕琪

（江西财经大学， 江西 南昌 330013）

引言

随着工业经济的发展，工业企业经济决策的科学性在企业发展过程中至关重要。工业经济的发展依赖于对自然资源的占有和有效配置，以何种批量进行工业生产、投资何种机器设备等问题是工业企业经常面临的经济决策问题。数学期望作为一种科学的工具，通过相关理论知识将经济问题量化为数学问题，能够大大提高工业经济决策的科学性与高效性。

1 数学期望的概念

数学期望是指在实验中每种可能的结果与其相应的概率相乘的总和，是一种最基本的数学特征，反应了随机变量的平均取值状况。数学期望通过对每次实验中的随机变量进行相关计算，用统计学与概率论的思维来描述随机变量的相关特征。

2 数学期望与工业企业经济决策的关系

2.1 数学期望提高工业企业经济决策的效率

工业企业的发展与工业企业管理者是否做出科学的决策息息相关。当工业企业管理者处于复杂环境背景下，数学期望的相关理论能够帮助企业管理者将经济问题来量化分析，通过一系列的数学计算，得出不同环境下的不同结果，并以计算结果作为决策标准，从而快速、高效、科学地解决复杂多样的经济问题。计算器、计算机等设备的使用更是加快了经济问题的处理效率。可见，数学期望通过量化分析经济问题，在保障决策科学性与准确的同时，大大提高了工业企业在复杂环境背景下经济决策的效率。

2.2 数学期望提高了工业企业经济决策的科学性

通过社会生活经验总结出的理论知识在实践中的应用，在一定程度上推动了人类对客观世界的认知和改造，数学正是一种通过分析事物间的客观规律来解决实践中具体问题的科学、高效、准确的工具。在经营管理活动中，工业企业管理者有时是用感性的思维来分析问题，进行经济决策时难免缺乏科学的理论指导，这使得不科学、不合理的执行结果在决策后时常发生，存在偏差或错误的决策结果严重影响了工业企业的正常经营。而数学期望的相关理论知识在工业企业经济决策中的应用，能够帮助管理者用科学、严谨的逻辑思维量化处理复杂的经济决策问题，从而使管理者能够做出科学的决策行为，大大提高工业企业经济决策的科学性。

3 数学期望在工业企业经济决策中的应用步骤

一般而言，数学期望在工业企业进行经济决策时，可以按照以下步骤应用：

3.1 确定经济决策的目标

确定经济决策的目标，是工业企业管理层运用数学期望进行经济决策的第一步。通过科学的筛选，以及综合考虑多方面因素，使企业管理层能够在特定条件与有效资源的约束下，做出可供选择的多种方案。

3.2 计算影响因素的概率

在多种备选方案中，工业企业管理层应该全面、系统地分析对经济决策具有影响作用的各种可控因素与不可控因素，在综合分析各种影响因素的基础上，运用数学期望方法计算出各种因素的概率，从而为下一步骤的计算提供数据支持。

3.3 计算企业预期收益值

在确定了不可控因素与可控因素等各类因素的发生概率后，工业企业管理者应依据统计学方法来计算企业收益值，并将该预期收益值与相应的概率对应。

3.4 选择最优决策方案

首先，工业企业应以预期受益值与对应的概率为数据材料，根据数学期望的计算方法，计算出不同方案的数学期望，并以数学期望的大小作为决策标准，从而选在出最优的决策方案，提高工业企业的管理效率[1]。

4 数学期望在工业企业经济决策中的应用案例

4.1 数学期望在工业企业最佳生产批量决策中的应用

最佳生产批量是指企业在成批生产中，使与之相关的生产费用最低的生产批量。工业企业在生产过程中，往往会遇到分几批进行生产、每批生产产品多少个是最经济合理的决策问题。以最佳生产批量进行生产，能够帮助企业付出最小的生产成本或收取最大的经营利润。数学期望在工业企业经济决策中的应用，能够帮助企业有效解决最佳生产批量这样的决策经济问题，期望利润是常用的比较指标。

例如：在进行明年生产量决策时，某工业企业通过分析以往的生产资料及市场销售情况，预测出市场销路差、中、好的概率分别为 0.2、0.5、0.3，大、中、小的生产批量分别用A、B、C表示。通过市场经验，明年销路状况与生产批量的关系如下表1所示。

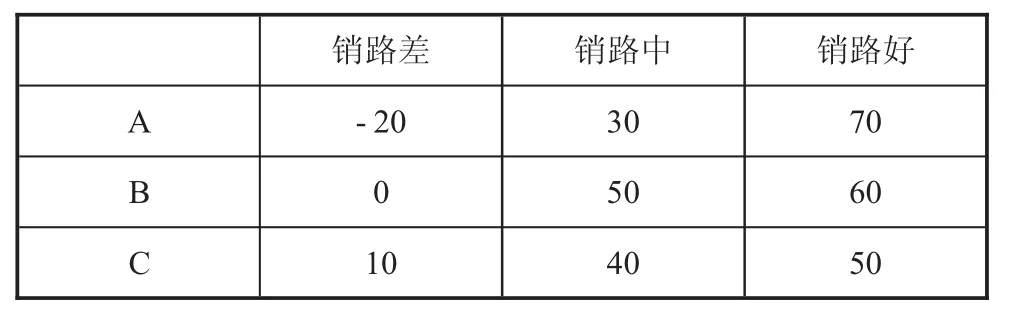
表1 A，B，C三者在不同销路状况的利润表 万元

通过分析，可以用数学期望法确定最佳生产批量，以预期利润P的大小作为决策标准中。

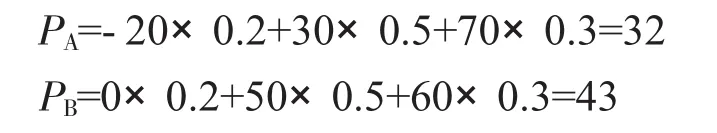
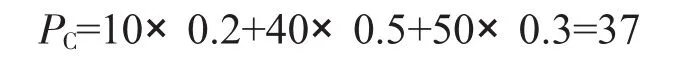
由于PB>PC>PA，生产批量B是该工业企业的最佳生产批量。

4.2 数学期望在工业企业投资决策中的应用

机器设备作为经营性长期资产，是工业企业发展的物质基础，机器设备更新换代是工业企业一项重要的投资决策。工业企业在发展过程中，往往会遇到对机器设备购置或维修等多种提高产能的投资决策方案。通过数学期望方法，管理者能够在综合各种可预见因素与不可预见因素的前提下，从各种方案中得到期望值最大的决策方案，为工业企业的发展做出最优投资决策[2]。

例如：某工业企业需要一台大型机床，企业管理者通过对市场上的a、b两种机床进行调研，了解到两种机床在相同环境下的次品数分别为c、d，通过分析长期产能表现，可得到c、d两种机床的次品个数及概率为如表2、3所示。

表2 c种机床的次品个数及概率

表3 d种机床的次品个数及概率

通过分析，可以运用数学期望来分别计算两类机床的次品率，将购置次品率E低的机床作为最优决策方案。

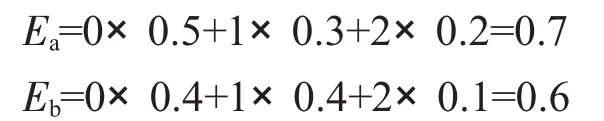
由于Ea