光伏电站模型对电力系统电压稳定性的影响研究
2018-08-14王韬喆
王韬喆
(上海展宇兴能光伏科技有限公司,上海 200040)
0 引 言
由于全球环境问题越来越突出,人们逐渐意识到保护环境、节约能源的重要意义。所以,清洁可再生资源逐渐受到越来越多人的重视。目前,清洁可再生能源转变为电能后,通常需要与传统电力系统并网运作,但并网后极易出现各种问题。为此,笔者在分析光伏电站模型的基础上,深入探讨电站模型对电力系统电压稳定性的影响,以期为促进我国电力事业的更好发展提供参考。
1 光伏电站模型分类
1.1 受控源模型
并网光伏电站与常规电源存在诸多差异。例如,光伏阵列拥有特殊的电压电流特性曲线,逆变器拥有最大功能点跟踪特性,输出功率较为随机且不连续。另外,由于光伏电站各部分电气量之间的控制关系较为明确,且各构成部分较为清晰,因此可融入受控电流源及受控电压源这两个概念,把整个系统看成由交流并网环节、逆变变和光伏阵列三部分构成的。逆变变如同控制量,变压器两侧如同受控源,而整流及逆变部分的电流及电压则由受控电流源与受控电压源代表。如此一来,整个系统便可得到有效的等效电效。然后,按照KVL、KCL定律即可得到相关的电压及电流方程。将二者整合起来,即为并网光伏电站的非线性时变方程组[1]。
在保持瞬时功率均衡的情况下,通过分析各电气量之间的关联和各构成部分的特性,可总结出受控源模型光伏电站的输出特征。图1为并网光伏电站等值简化模型,图2为受控源模型的等效电路图。
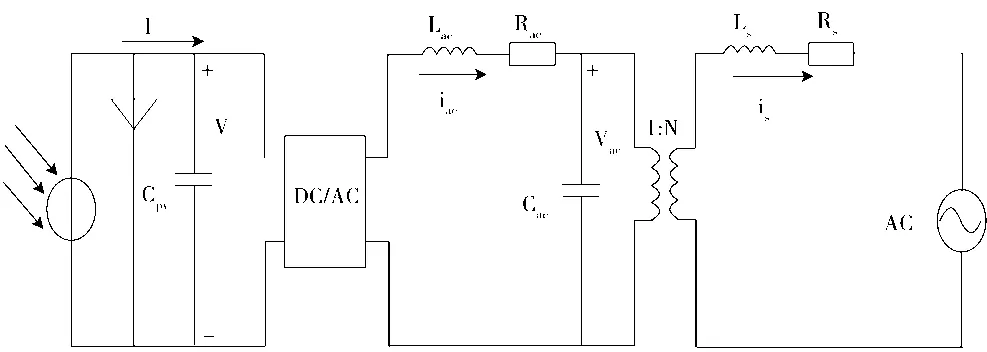
图1 并网光伏电站等值简化模型
分析图2(a),遵循KCL定律,即可得出电流方程式:
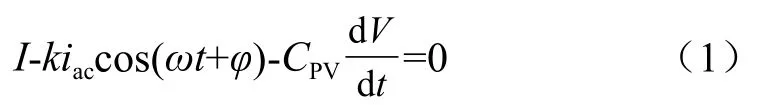
式中ω代表工频角速度,φ代表逆变器的调制相位角,k代表逆变器的调制深度。
端电压V与输出电流I之间的关联为:
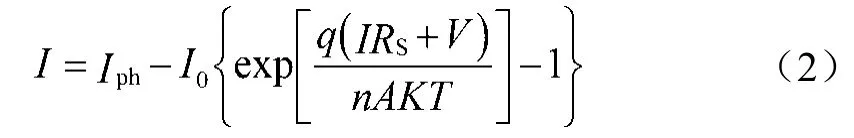
式中Iph代表光生伏打效应的电流;I0代表二极管的反向饱和电流;I代表光伏电池输出的电流;V代表端电压;S代表光照强度;A代表二极管的品质质因;q代表电子包含的电荷量,取值1.6;K属于常数,取值为1.38[2]。
遵照KCL与KVL定律,结合图2(b),可将电流、电压方程总结如下:
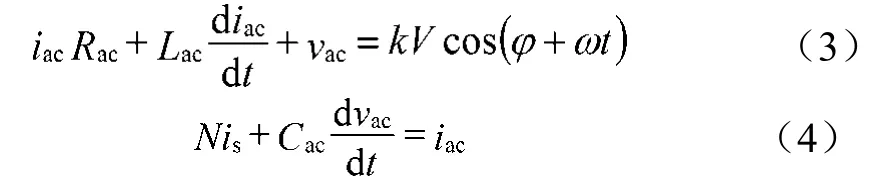
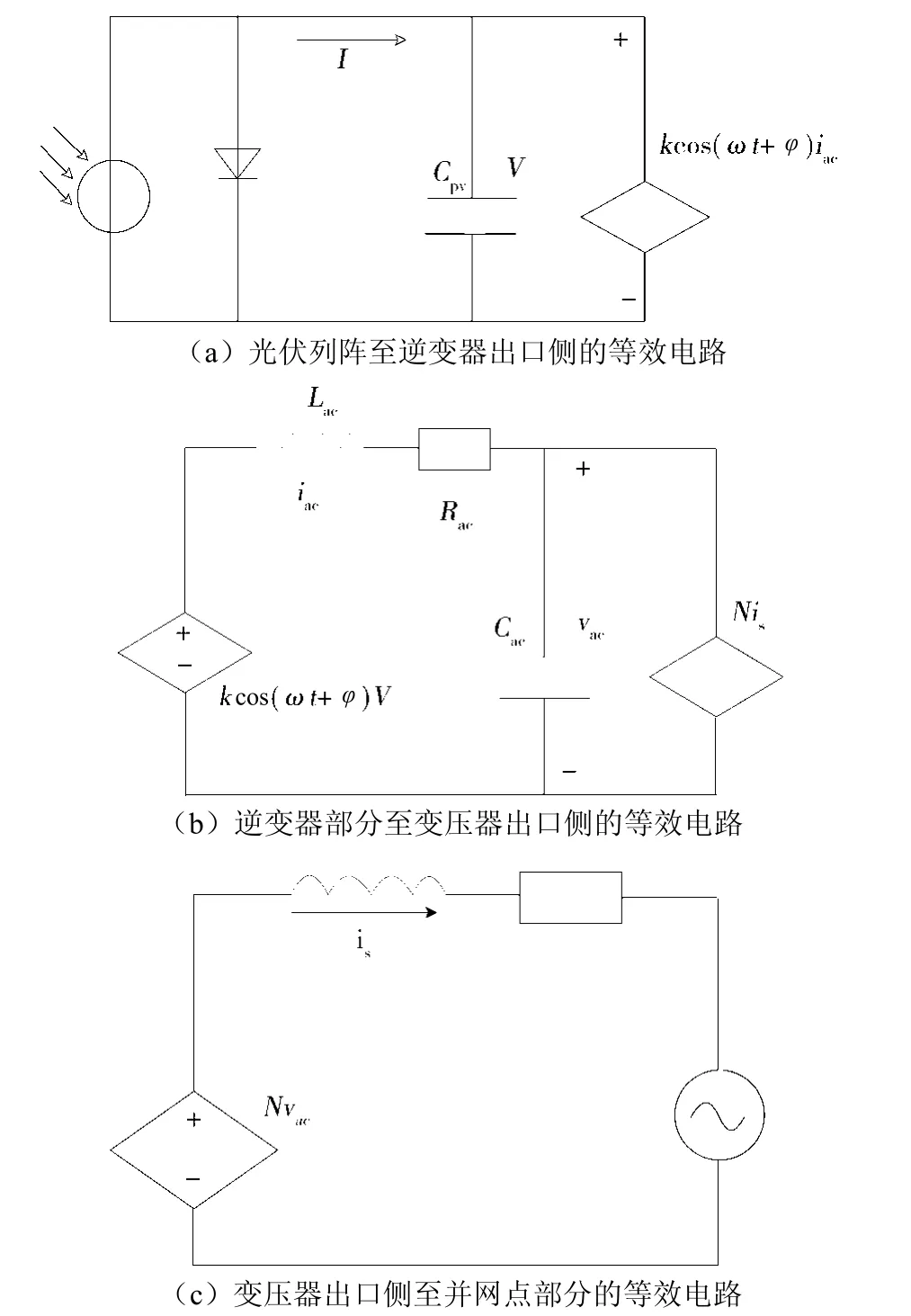
图2 受控源模型的等效电路图
遵照KVL定律,结合图2(c),可将电压方程总结如下:
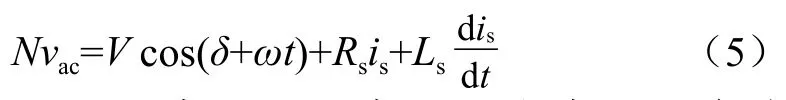
以上式(1)、式(3)、式(4)和式(5)充分体现了并网光伏电站的动态特征。
倘若用y代表sinωt,用x代表cosωt,可由式(6)来代表上述模型:
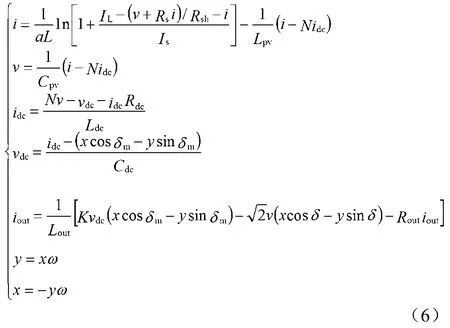
1.2 小信号模型
图3为小信号模型采用的系统,主要包括单L滤波装置、Boost DC/DC升压变换器、光伏阵列以及DC/AC逆变器等。由于实际容量要求,将光伏电池组件以串并联的方式形成了光伏阵列,通过光生伏打效应来实现太阳能向直流电能的转变。然而,不同的光照时间和光照强度下,它输出的有功功率也会有所不同。有功功率与输出电压呈明显的非线性关系,因此系统应对其实施最大功率点跟踪(MPPT)控制,以确保输出有功功率最大化[3]。DC/AC逆变器能够实现从直流电向交流电的转变。由于谐波普遍存在于逆变后的交流电中,所以必须对其实施滤波处理,而这主要依靠电感来完成,且可获得功率因数为1的功率,再将之与电网相并。Boost升压电路不仅可以使直流电压变大,而且可以做到对系统最大功率点的有效跟踪。
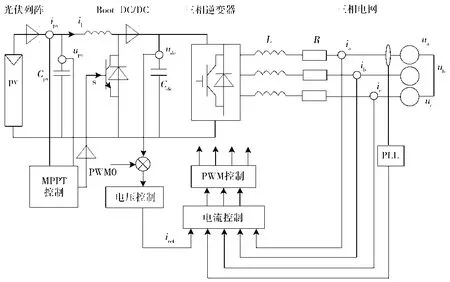
图3 光伏发电并网系统的结构示意图
1.2.1 主电路模型
可通过式(7)表示直流稳压电容和Boost升压变换器的状态方程:
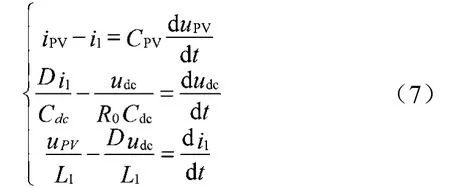
逆变器交流侧的状态方程及变换dq坐标后的方程可表示为:
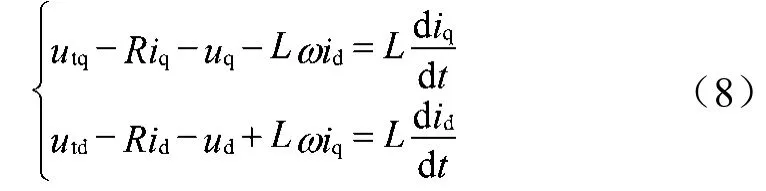
对式(7)和式(8)实施线性化处理,可得到:
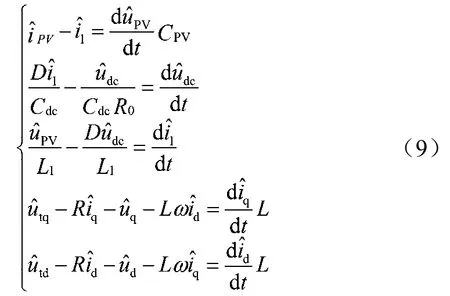
1.2.2 光伏输出电压控制模型
光照时间与光照强度等因素的干扰,光伏阵列的输出功率极易发生变化,存在较大的不确定性。所以,若想使光能得到最大限度的利用,必须对其实施最大功率点跟踪(MPPT)。现阶段,主要是通过扰动观察法、电导增量法和恒压法来跟踪计算最大功率点,且以上方法均较为有效。光伏输出电压的控制框架图见图4。
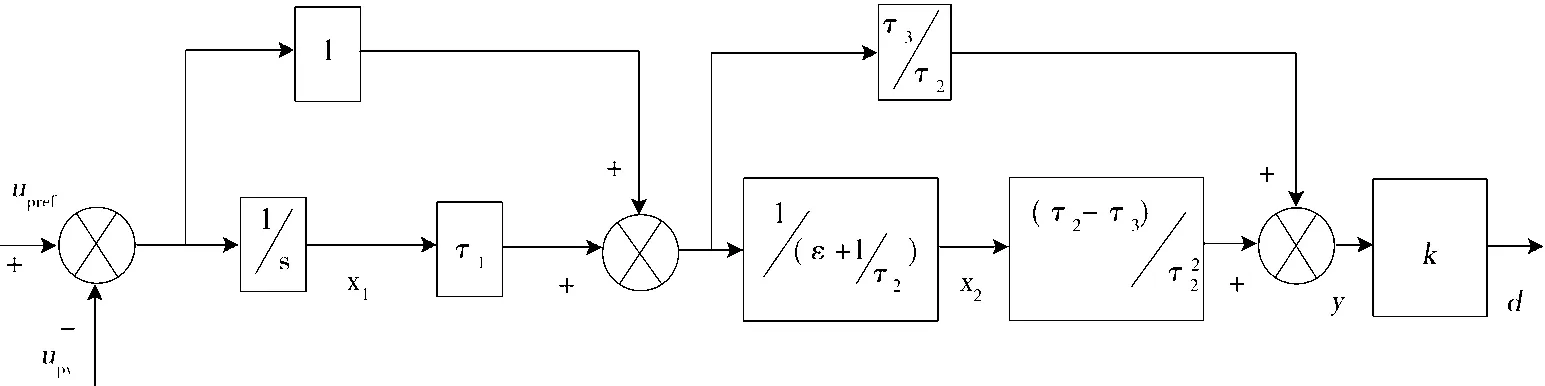
图4 光伏发电系统输出电压的控制框图
通过分析图3可总结出:
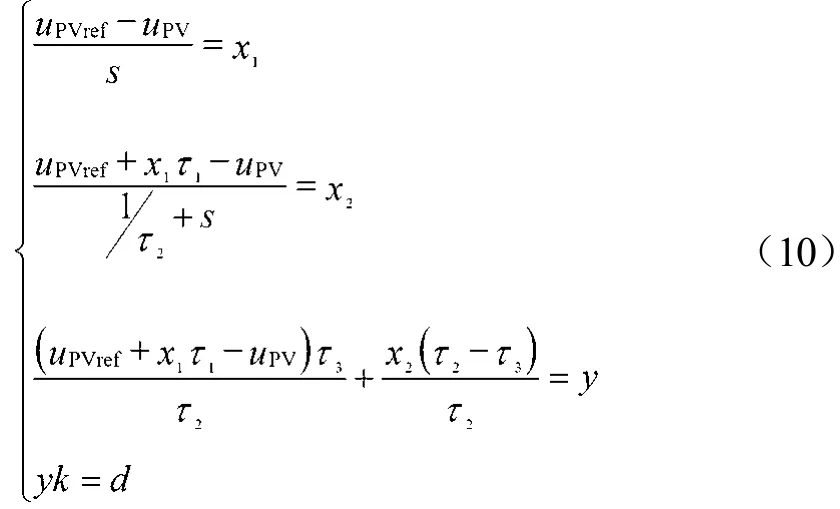
式中τ1、τ2、τ3分别代表PIA控制器的参数;x1和x2分别代表状态变量。
对式(10)实施线性化处理,可得出:
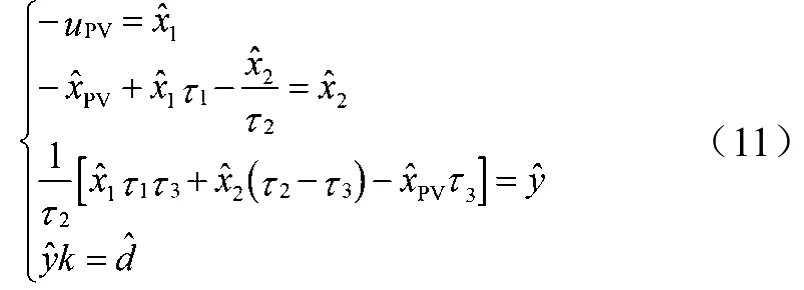
式(11)代表着光伏电站输出电压控制器的小信号模型。
1.2.3 电流内环电压外环的模型
如果采用电压外环、电流内环控制模式的光伏并网逆变器,即电流内环控制图见图5(a)。可通过前馈式的解耦控制方法进行计算。采取电流内环的控制模式,可以使并网时的功率因数控制在1,可利用系统实时控制逆变器的实际输入电流值。因为此系统的无功电流和有功电流之间属于耦合关系,可通过dq同步旋转坐标系下逆变器的数学模型进行分析,增加了控制器的设计难度。图5(b)为电压外环的控制图,能够实现对直流侧电压值的实时控制,以免其出现波动。通过将设定的参考电压值与直流侧母线的实际输入电压值进行对比,再在调节器中录入对比结果,调节后便可得到指令电流值。
通过分析图5,可总结出:
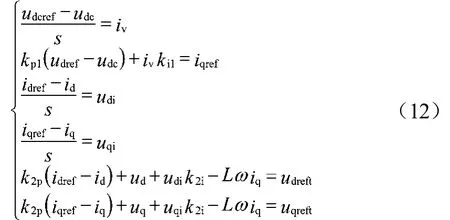
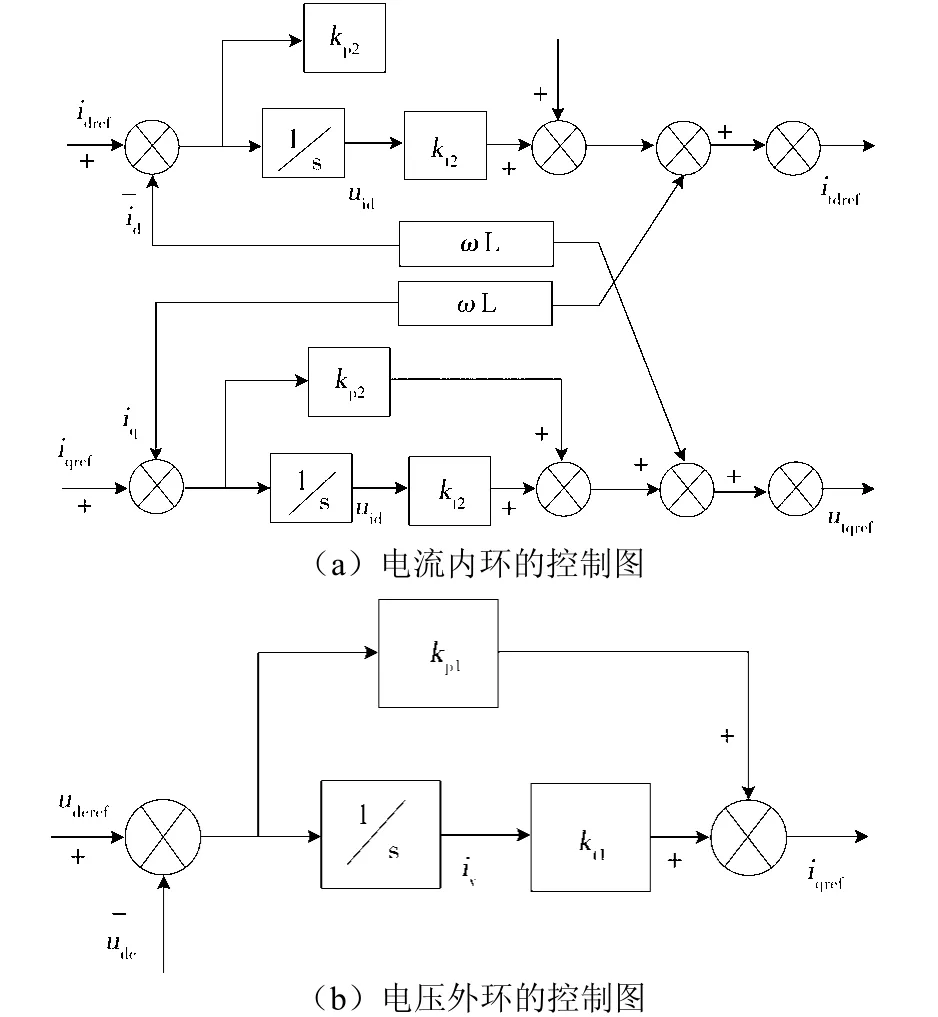
图5 控制框架图
通过对式(12)实施线性化处理,可得出:
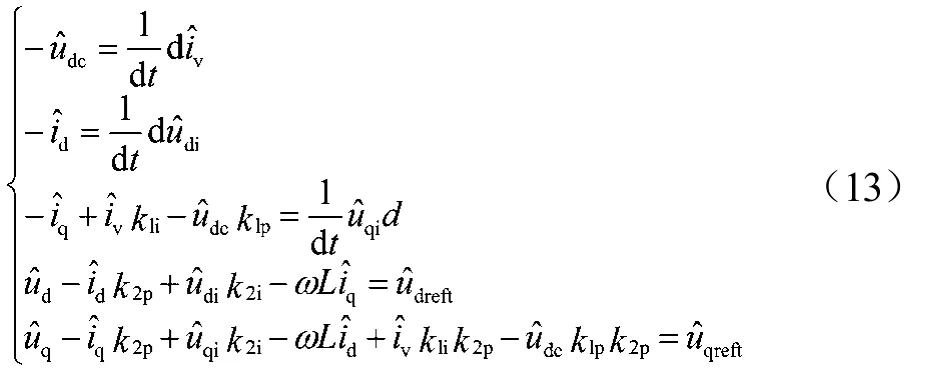
假定udpreft=udpt,可得出:
1.2.4 光伏电站的整体小信号模型
将式(11)、式(13)、式(14)整合,可得到系统的整体小信号模型:

式中,有:
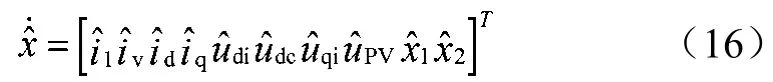
1.3 简化模型
光伏发电系统由诸多高频开关元件组成。因为它具有非线性特点,所以详细器件模型在仿真分析复杂并网系统时无法得到有效使用。对之前的详细器件模型实施简化处理,以此简化计算、提升速度,此模型即为简化模型。逆变器具有非线性特点,所以会在很大程度上干扰光伏发电站的正常运作。所以,本文对其他非线性部分进行了简化处理,只是将逆变器造成的影响作为考虑重点。该简化模型可表示为:
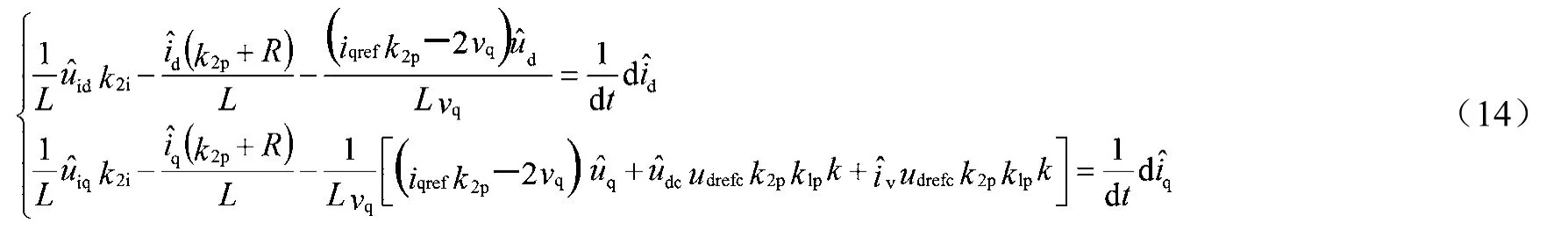
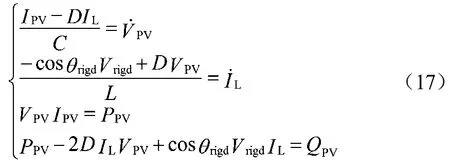
通过分析以上三种光伏电站模型发现,小信号模型是根据系统整体构建的一种模型。具体的,可通过对滤波器、逆变器以及光伏阵列等各部分分别建模,以此构建系统的整体模型。该模型能够将光伏发电并网系统的整个过程清晰、详尽地展现出来,但也有一些缺陷,如较为繁琐,无法准确地判断出繁琐的光伏发电并网系统的特点。受控源模型主要通过增加受控电压源、受控电流源,始终围绕光伏阵列适当简化控制系统构建的一种模型。此种模型的构建思路较为明了,可清楚反映不同部分电气量之间的控制关联性,也可以充分体现不同环境条件下系统的变化情况[4]。简化模型是逆变器构建的一种系统等值模型,主要通过简化逆变器两侧的器件获得。这种模型结构明了,能够充分体现核心元件的特征,但其协调性较差,无法充分体现出光伏发电系统各部分的特征。
2 光伏发电并网系统的电压稳定理论概述
影响光伏发电并网电压稳定的因素主要包括两种,一是光伏输出功率的改变,二是无功、有功负荷的改变。图6为光伏发电并网等效电路图,光伏发电部分与并网系统之间的电抗由X1代表;R1代表电阻;并网电力系统的电压向量由V代表;变压器出口侧的电压幅值由E表示。
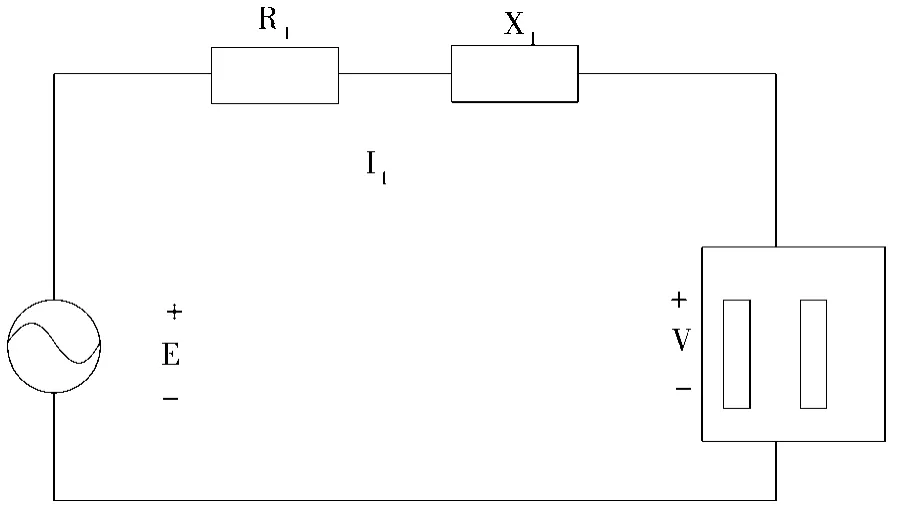
图6 光伏发电并网等效电路图
图7、图8分别为有功电流、无功电流对电压的作用向量图。Ir代表并入系统后无功电流的向量,Ia则代表并入系统后有功电流的向量。因为中间逆变器的电流发生了改变,所以无功电流远远小于有功电流,无功向量有时甚至为0。通过分析图7可知,有功电流Ia在电阻R1上存在电压降R1Ia,是造成系统电压减小的一个重要原因。但是,因为系统电压V与jX1Ia互相垂直,再加上其值并不大,故其给电压下降造成的影响可忽略不计。通过分析图8不难发现,无功电流Ir在电感X1上存在的电压降jX1Ir是造成电压下降的另一个重要原因。由于电压V与R1Ir互相垂直,所以其给电压下降造成的影响也可忽略不计。
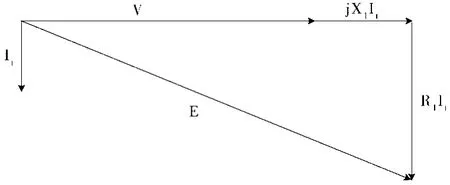
图7 有功电流对电压的作用向量图
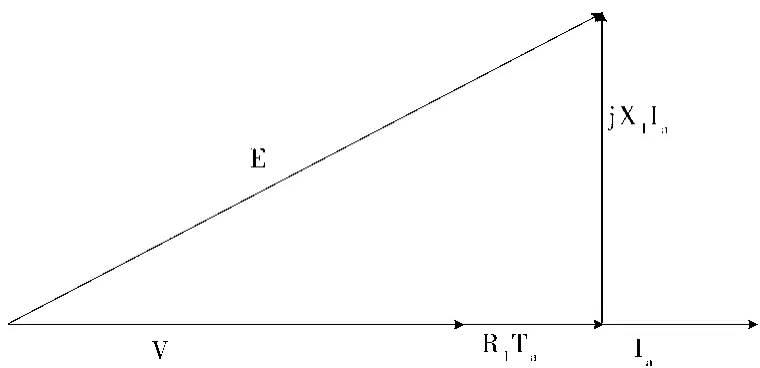
图8 无功电流对电压的作用向量图
3 三种光伏电站模型对电力系统电压稳定性的影响
图9、图10分别是三种光伏电站模型下负荷母线电压随负荷有功功率改变、电站输出有功功率改变的分岔图。
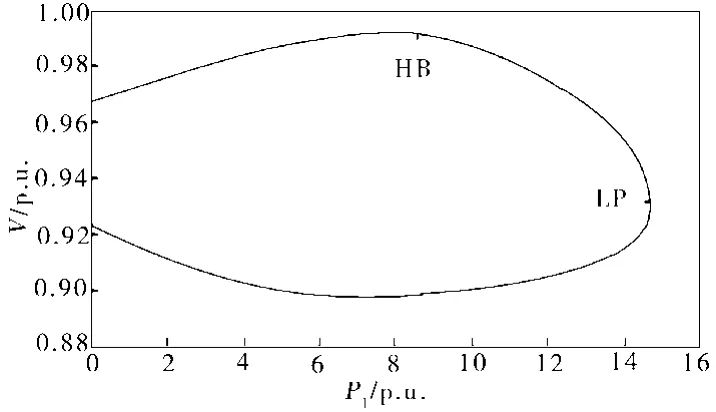
图9 负荷母线电压随负荷有功功率改变的分岔图
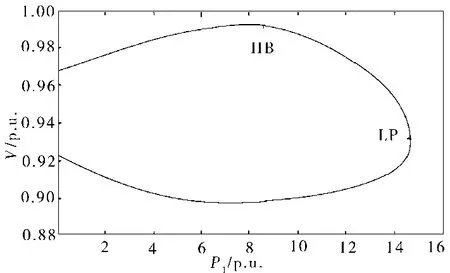
图10 负荷母线电压随电站输出有功功率改变的分岔图
通过分析发现,在光伏发电并网系统和理论、分析工具相同的情况下,倘若所选用的光伏电站模型不同,其分析结果也会有所差别,但其鞍结分岔点却是相同的。本文通过分岔理论来分析光伏电站并网系统给电压稳定性造成的影响,如果采用不同的光伏电站模型,其系统常微分方程也是有所差别,故其获得的分岔结果也有所不同。尽管分析结果会因所采用的光伏电站模型不同而出现细微改变,然而三种光伏电站模型均具备一个相同的特性。由此可见,光伏电站模型对光伏发电并网系统电压的稳定的定性特点无太大影响。总而言之,通过分岔理论对电力系统的电压稳定性进行研究时,可随意采用光伏电站模型,并不会影响其定性分析结果。然而,由于简化模型只有考虑到逆变器的影响,而省去了其他非线性动态部分,所以如果需要对电力系统电压稳定性进行动态分析,切不可采用简化模型。
4 结 论
综上所述,光伏电站模型主要包括三种,即受控源模型、简化模型以及小信号模型。通过分析发现,影响光伏发电并网电压稳定的因素主要是光伏输出功率的改变以及无功、有功负荷的改变。当光伏发电并网系统相同时,如果选用的光伏电站模型不同,所得到的分岔结果会存在一定差异,但不会影响光伏发电并网系统电压的稳定的定性特点。所以,建议可采用简化模型来定性研究光伏电站并网对电力系统电压稳定性的影响以简化计算、提高速度。
