基于生成树的学生互校验签到应用研究
2018-08-13王芳,蔡沂
王 芳,蔡 沂
基于生成树的学生互校验签到应用研究
王 芳,蔡 沂
(华南理工大学 广州学院计算机工程学院,广东 广州 510800)
文中提出了一种课堂签到方案,主要思路是通过学生座位信息之间的相互校验来验证签到的真实性。首先,文中描述了该签到方案的工作流程;然后设计了基于生成树的相互校验算法;最后分析了该签到方案的优势。分析和测试结果表明:该签到方案能够快速产生签到结果、防止代签、减少迟到早退;基于该方案的签到系统实现简单,具有很强的实用性和推广价值。
签到;生成树;选座;相互校验;考勤
0 引言
大学课堂签到可以粗略地分为人工签到和自动签到两类。人工签到或点名不仅消耗了课堂时间,而且具有较大的局限性,迟到、早退、代签等现象时有发生。随着移动互联网技术的发展,近年来涌现出大批手机签到系统,如使用无线局域网和手机IMEI的签到系统[1]、使用蓝牙技术和二维码技术的点名软件[2]、基于微信公众号的签到[3]、基于WIFI的室内定位签到[4]、基于WIFI热点和MAC地址的手机签到[5-6]、基于GPS定位的签到[7-8]等,但都存在无法精确判断学生是否在教室内、是否签到后离开等问题。还有些方案依赖于特定的手机操作系统和网络设备的支持,在学校推广和普及的难度较大。
本文提出一种基于生成树的学生互校验签到方案。该方案要求学生在规定时间内提交自己的座位号,并且通过扫码获取前后左右的位置信息。系统通过课堂上所有签到学生位置信息之间的相互校验生成签到座位表,签到座位表直观地展示了学生的入座情况,方便教师使用手机快速查看和操作。为缩短签到位置信息的校验时间,本文提出一种基于生成树的相互校验算法。最后,文章分析了基于本方案的课堂签到系统的优势。
1 系统设计与功能描述
本文针对大学课堂准确并快速签到设计一种签到方案,能较大程度上避免学生抱着侥幸心理逃课、迟到、早退。主要包括学生选座、教师考勤、学生确认入座、系统校验签到信息、系统生成签到座位表、教师管理考勤记录等功能,所有操作都在手机上完成。图1给出了此课堂签到方案的工作流程图。
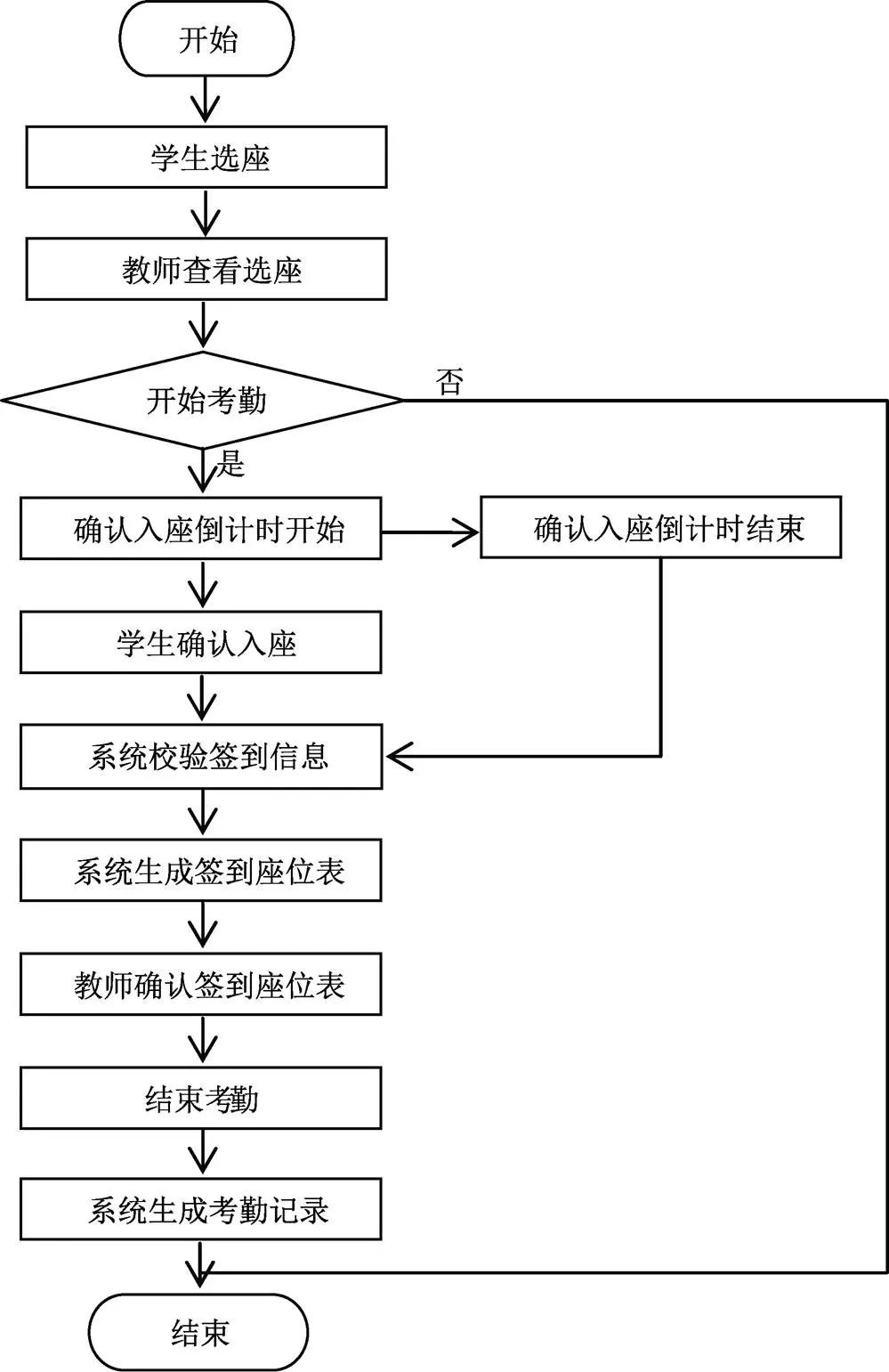
图1 系统工作流程
功能描述如下:(1)学生选座:学生选择即将要上的课程,进入对应教室座位表页面选座;(2)开始考勤:教师选择正在上的课程,进入对应教室座位表页面查看选座情况,可开始考勤;(3)学生确认入座:教师开始考勤后,教室座位表页面显示确认入座倒计时,学生通过扫码提交前后左右同学的位置信息完成确认入座;(4)系统校验签到信息:确认入座倒计时结束,系统通过所有学生位置信息的相互校验得出每个学生的签到结果;(5)系统生成签到座位表:系统根据签到结果将签到有效的学生姓名显示在教室座位表上;(6)教师确认签到座位表:教师查看签到座位表,并可修改签到座位表以应对特殊情况;(7)结束考勤:教师点击结束考勤按钮表示完成本次课堂考勤,系统保存本次课堂考勤记录;(8)管理考勤记录:课后学生可查看自己的考勤记录;教师可管理相关课程的考勤记录,教师还可以登录PC端后台完成考勤记录的统计、汇总和导出等。
2 互校验签到理论依据与算法设计
2.1 座位表与选座
大学教室座位一般为m*n型,m为座位行数,n为座位列数。作者所在的学校已存在教室座位表系统,可直接使用。每个座位的座位号按行号和列号来编排,i-j表示第i行第j列座位的座位号(1≤i≤m, 1≤j≤n)。图2为一个8行8列教室座位示意图。

图2 教室座位表
Fig.2 Classroom seating chart
学生上课之前,根据课程信息进入相应教室座位表页面选座。图3为某堂课选座座位表,灰色表示该座位已被某学生选中。

图3 选座座位表
每个选座的学生都将产生一条如表1所示的选座记录。表中省略了与课程相关的教室和上课时间等信息,本文暂不讨论签到记录与课程相关信息的关联。
2.2 确认入座与位置信息
上课后,教师可开始考勤,学生需要确认入座。
表1 选座记录

Tab.1 Seat selection record
一次有效的签到需要得到邻座同学位置信息的证明,确认入座是为了让学生提交其前后左右位置同学的信息(学生通过扫描邻座同学的二维码来提交其位置信息)。由于方向的相对性,当某学生的前方位置有人时,他把前方学生的信息填入自己的‘前位’中,同时他也将被前方位置的学生填入其‘后位’中;当某学生的左方位置有人时,他把左方学生的信息填入自己的‘左位’中,同时他也将被左方位置的学生填入其‘右位’中。左右位置与前后位置同理,不再累述。
系统可设置确认入座时间段,比如学生必须在教师开始考勤后的5分钟内完成确认入座操作。在确认入座时间段内,已选座的学生还可以重新选座(换座)。学生要确保自己前后左右至少有一个位置有学生坐,这样才能被他人填入位置信息中,才能使自己得到校验。学生在确认入座时填写位置信息后将产生一条如表2所示的位置信息记录。
表2 某学生的位置信息记录

Tab.2 A student's location information record
表2为学生‘周围’的位置信息记录。根据表2以及前后左右座位的特点,可以由学生‘周围’确认入座的位置信息得到表3所示的座位对应关系。
表3 由表2得出的学生座位对应关系

Tab.3 The seat correspondence of students is obtained from table 2
用表3的座位对应关系与表1的选座记录进行对比,不仅校验了学生‘周围’的签到记录,同时也校验了学生‘张倩’和‘李悠’。由此可知,并不需要所有的学生都提交前后左右的位置信息,有些学生是主动验证,如学生‘周围’;有些学生是被动验证,如学生‘张倩’和‘李悠’。
接下来我们要讨论的问题是:如何利用最少的位置信息验证选座座位表中所有位置的签到记录。
2.3 位置信息的数学表示
2.3.1 无向图
定义1 无向图G=
若将选择座位号i-j的学生看成顶点vi, j,图3的选座座位表可转化为图4。

图4 顶点化的选座座位表
若用座位前后左右的相邻关系表示边,则可能与顶点vi, j有关的边为(vi–1, j, vi, j)、(vi, j, vi+1, j)、(vi, j–1, vi, j)、(vi, j, vi, j+1),其中1≤i–1, i, i+1≤m,1≤j–1, j, j+1≤n。因此,图4的选座座位表可表示成一个非连通的无向图G,G有3个连通分量:G1、G2、G3,如图5。
由此可得,所有的选座座位表都可以表示成类似图5的无向图,连通分量的个数大于等于1。又因为每个学生的前后左右至少有一个位置有同学坐,所以每个连通分量至少包含2个顶点。
2.3.2 生成树
引理1 如果连通图 G的一个子图是一棵包含G的所有顶点的树,则该子图称为G的生成树(Spanning Tree)。生成树是连通图的包含图中的所有顶点的极小连通子图[10]。
引理2 若G是非连通的无向图,则要若干次从外部调用DFS(Depth First Search深度优先搜索)或BFS(Breadth First Search 广度优先搜索)算法,才能完成对G的遍历。每一次外部调用,只能访问到G的一个连通分量的顶点集,这些顶点和遍历时所经过的边构成了该连通分量的一棵DFS或BPS生成树。G的各个连通分量的DFS或BFS生成树组成了G的DFS或BFS生成森林[10-11]。

图5 无向图G,连通分量G1、G2、G3
由引理1和引理2可知,对于由选座座位表转换成的无向图G,通过对G的遍历找到G的每个连通分量的生成树,就找到了每个连通分量中连接所有顶点的最短连通路径。
图的生成树不惟一。从不同的顶点出发进行遍历,可以得到不同的生成树。[11]对于图5中无向图G的连通分量G3,若从顶点v6,1出发进行遍历,图6为G3的一棵生成树,v6,1为树的根节点。
对于图5生成树中的节点,只要父节点位置所代表的学生提交其子节点位置的学生信息,就可以完成对图中8个节点位置所代表的学生签到信息的校验。
2.4 位置信息的收集
根据生成树中节点之间的父子关系和节点本身的位置关系,系统向每个选座的学生发送收集位置信息的指令。由图6和表4,座位号6-1的学生接收到的指令为“请提交后方和右方同学信息”,座位号6-2的学生接收到的指令为“请提交前方和右方同学信息,并将你的信息提供给左方同学”,座位号8-2的学生接收到的指令为“请将你的信息提供给左方同学”,诸如此类。根据指令收集到的位置信息如表5所示。

图6 连通分量G3的生成树
表4 图6树的父子节点关系

Tab.4 The parent-child relationship of the tree in figure 6
表5 收集的位置信息

Tab.5 Collected location information
如果选座座位号为5-2的学生没来,那么他将不会出现在座位号为6-2的学生的前方位置信息中。
如果选座座位号为8-2的学生没来,那么他将不会出现在座位号为8-1的学生的右方位置信息中。而座位号为8-1的学生收到了“请提交右方学生信息”的指令却无信息可填,此时8-1的学生应填写有人坐的一个方向的同学信息来证明自己的存在(因为每个学生的前后左右至少有一个位置有同学坐,这是学生确认入座的必要条件)。座位号8-1的学生应提交补充信息“前方同学的信息:XXX”。
如果选座座位号为7-1的学生没来,那么他将不会出现在座位号为6-1的学生的前方位置信息中。而座位号为7-2的学生收到了“请将你的信息提供给左方同学”的指令,当他发现自己的信息无法被填入时(左方位置7-1无人),应填写有人坐的一个方向的学生信息来证明自己的存在。座位号7-2的学生应提交补充信息“前方同学的信息:XXX”或“后方同学的信息:XXX”。
由此可知,对于由选座座位表转换成的无向图G的生成森林,只要生成树中每个父节点位置所代表的学生填写其子节点位置的学生信息,且当有节点发现自己的信息无法被填入并且也没有接收到填入他人信息的指令时能填写补充信息来证明自己,就能收集到足够的位置信息与选座座位表进行对比校验,得出签到结果。收集位置信息的过程即为获取签到记录的过程,校验位置信息的过程即为验证签到真实性的过程。
2.5 基于生成树的互校验签到算法设计
为了获得足够的位置信息与选座座位表进行对比校验,系统要向选座的学生发送收集位置信息的指令。要向哪些学生发送指令?分别给他们发送什么样的指令呢?这两个问题才是获取位置信息的关键所在。
算法1 基于生成树的互校验签到算法。
第1步:根据选座座位表生成无向图G
第2步:调用DFS(或BFS)算法遍历无向图G,生成森林
第3步:对生成森林中的每棵生成树,根据树的生成路径,调用generateOrders算法(见算法2)生成要发送给每个节点的指令
第4步:向每个节点表示的学生发送对应的指令
第5步:获取学生根据指令提交的位置信息
第6步:将位置信息与选座座位表进行对比,生成签到座位表
算法1第3步中对每棵生成树调用名为generateOrders的算法:数组nodeArr[]用于存储其生成路径的节点信息,是算法1第2步的输出;哈希表orderMap
算法2generateOrders生成指令算法。
for each fnode in nodeArr[]
for each snode in sonArr[]
orderList_of_fnode.add(orderStr_of_fnode), orderList_of_snode.add(orderStr_of_snode)//将前面构造的指令字符串添加到对应的指令列表中
orderMap.set(fnode, orderList_of_fnode), orderMap.set(snode, orderList_of_snode)//分别更新orderMap中key为fnode和snode的value
end for
end for
通过调用算法2,哈希表orderMap
3 系统分析与实现
3.1 算法时间复杂度
算法1第2步,调用DFS和BFS算法遍历无向图G,若用邻接矩阵来实现,时间复杂度均为O(n2),其中n为顶点数。
算法1第3步,对每棵生成树调用算法2。因为每棵生成树至少有2个节点,所以生成树的数量一定小于n/2。而算法2中,因为每个节点最多有4个子节点,所以时间复杂度为O(n*4)。因此,算法1第3步的时间复杂度为O(n*4*n/2)=O(n2)。
算法1第6步,将位置信息与选座座位表进行对比,时间复杂度也为O(n2)。
因为算法1的时间复杂度集中体现在第2步、第3步和第6步,所以基于生成树的互校验签到算法的时间复杂度为O(n2)[11]。
n为顶点数,即为一堂课上的学生数量。大学课堂一般为两个行政班合并为一个教学班,人数在120人左右,对于时间复杂度为O(n2)的算法都能很快执行完毕。算法1第4步为发送指令,第5步为表单提交,系统可设置学生必须在发送指令后的5分钟内完成确认入座。
3.2 实现确认入座
为了防止签到作弊,教师开始考勤后,系统给每个选座的学生生成限本次考勤使用的二维码,并设置有效时间,学生通过扫描二维码来获取指令中要求提供的邻座同学的位置信息。如座位号6-1的学生接收到的指令为“请输入后方和右方同学信息”,表示他要扫描后方和右方位置同学的二维码;座位号6-2的学生接收到的指令为“请输入前方和右方同学信息,并将你的信息提供给左方同学”,表示他要扫描前方和右方位置同学的二维码,并将自己的二维码提供给左方位置的同学扫描。
3.3 获得签到座位表
将学生在确认入座时间段内提交的位置信息与选座座位表进行对比校验,可得出签到座位表如 图7。

图7 签到座位表
教师可查看并修改签到座位表,以应对特殊情况的出现。如有学生忘带手机,教师可帮学生签到。当教师认为不再需要修改签到座位表时,可确认签到座位表以完成本次考勤。
3.4 非正常签到分析
开始考勤后,系统向选座的学生发送收集位置信息的指令,学生根据指令提交位置信息以确认入座,学生必须在规定时间段完成确认入座。教师可自主选择考勤的时间,迟到或早退的学生很可能不能按时完成确认入座,也就无法签到成功。
系统根据选座记录和确认入座记录快速生成签到结果,教师可以实时查看签到座位表。教师在确认签到座位表之前可以修改签到座位表,如教师在上课过程中发现有位置完成签到却无人,可判断为早退,可点击相应座位取消其签到或修改成早退状态。
4 结语
本文提出基于生成树的学生互校验签到方案,利用学生之间的位置信息进行相互校验,不但提高了签到的效率,而且保证了签到的真实性。基于该方案的签到系统不依赖除手机之外的其他设备、不限于某种手机操作系统。系统全部采用web实现,使它能快速集成到如微信、智慧校园、课程表等其他学生广泛使用的应用系统或平台中,具有很强的实用性和推广价值。
签到的前提是选座,类似于电影院选座。对于一些有较多学生感兴趣、教师授课方式生动的课程,可能会出现“前排抢座”现象,在线选座也达到了在线抢座的目的。从心理学的角度来说,选座(抢座)行为可以提高学生上课的积极性。[12]
签到活动的第二步是确认入座,由教师主动发起。教师可根据实际情况决定是否对本堂课考勤,开始考勤才会有确认入座流程。签到活动由学生通过互动完成,确认入座增强了学生签到的主动性,是一种积极的心理暗示。
大学课堂的座位选择与教学情况紧密相关。教师预览系统生成的签到座位表,可以加深教师对学生的了解,使教师更好地把握课堂教学。系统将累计产生大量选座数据,这些数据不但可以用来分析学生上课时的座位分布对学生成绩的影响[13],而且可以分析教师的授课形式和授课质量对学生学习积极性的影响。分析学生上课时的座位分布对学生成绩的影响,让老师更加了解学生,对成绩不好的学生进行劝导;分析教师的授课形式和授课质量对学生学习积极性的影响,让老师对自己的教学方式和手段进行反思,推动教学改革。[14]
[1] 刘冬梅, 任亚平, 周杰等. 基于Android的手机签到系统[J]. 科技资讯, 2017, 14: 17-18.
[2] 陈三清, 殷鹏. 基于Android手机的课堂点名软件设计与实现[J]. 电脑知识与技术, 2017, 7, 95-99.
[3] 陈东伟, 谭建新, 温家成等. 基于微信的考勤信息管理系统设计与实现[J]. 信息技术, 2017, 5, 85-88.
[4] 蒋航, 蔡秋枫. 基于室内定位的学生签到系统设计[J]. 电脑知识与技术, 2017, 1, 54-55.
[5] 赵靓, 张玉. 基于WIFI热点的手机签到系统设计[J]. 计算机编程技巧与维护, 2017, 6, 59-61.
[6] 肖俊生, 刘俊娟. 基于WI-FI的学生考勤系统研究与设计[J]. 工业控制计算机, 2017, 1, 114-115.
[7] 张劲波, 周泽崇, 李雅杰等. 基于Android的上课签到软件分析与设计[J]. 电脑编程技巧与维护, 2017, 2(3), 28.
[8] 徐宁. 基于微信平台的并行签到考勤管理系统[J]. 电脑知识与技术, 2016, 30, 77-79.
[9] 耿素云, 屈婉玲, 张立昴. 离散数学[M]. 北京: 清华大学出版社, 2013.
[10] 李明哲等. 图论及其算法[M]. 北京: 机械工业出版社, 2010.
[11] 严蔚敏, 吴伟民. 数据结构(C语言版)[M]. 北京: 清华大学出版社, 2011.
[12] 王会廷, 张艳平, 阎慧. 大学生课堂行为的心理学研究[J]. 安徽工业大学学报: 社会科学版, 2012, 29(3): 37-38.
[13] 王映学, 段宝军, 张晓州. 大学课堂座位选择与学业成绩的关系研究[J]. 重庆高教研究, 2017, 5(3): 65-72.
[14] 程永佳. 大学课堂有效教学的影响因素及提高策略[J]. 教育与教学研究, 2012, 26(5): 22-25.
Research on Class Sign_in Application Based on Validation between Classmates using Spanning Tree
WANG Fang, CAI Yi
(Guangzhou College of South China University of Technology, Guangzhou 510800, Guangdong, China)
In this paper, we put forward a class sign-in solution which verify the authenticity of sign-in by the seat information of classmates. Firstly, the work flow of this solution is described; secondly, the mutual validation algorithm based on Spanning Tree is described; finally, the greatest strengths of our solution are analyzed. Analysis results and test results show that using our solution can produce accurate sign-in results, prevent cheating, reduce arrive late and leave early, and the class sign-in system based on our solution is simple and very practical and has strong promotional value.
Class sign-in; Spanning Tree; Seat selection; Mutual validation; Attendance
TP311
A
10.3969/j.issn.1003-6970.2018.07.002
广东省高等学校特色专业建设项目(JY170102)
王芳(1986-),女,助教,主要研究方向:软件工程、大数据技术;蔡沂,(1978-),女,副教授,主要研究方向:网络工程、信息安全。
本文著录格式:王芳,蔡沂. 基于生成树的学生互校验签到应用研究[J]. 软件,2018,39(7):06-11
