工程灾害救援环境中仿人机器人下蹲取物动力学分析
2018-08-10王士革申晓伟
王士革,卢 闯,申晓伟,王 建
(信阳师范学院 建筑与土木工程学院,河南 信阳 464000)
0 引言
仿人机器人是机器人领域中重要而尖端的研究方向之一,然而仿人机器人是一个多自由度、非线性、并且具有复杂运动和动力特性的系统[1,2].仿人机器人在复杂多变的环境中拥有着很好的移动性能,如穿越崎岖地形、斜坡与楼梯等,这种移动性是非常重要的.为了避免仿人机器人在复杂环境中行走失稳摔倒,肖乐等[3]结合FZMP的在线调整策略,提出了通过控制直立姿态、调整落地角动量、落地减振和落地位置,进而改变髋关节的高度来吸收由摆动腿提前着地而产生的垂直振动.朱洪波在其博士毕业论文中开展了基于力/力矩反馈的仿人机器人动态平衡行走控制方法研究,提出了基于扩展时域被动的摆动脚软着陆控制方法,并通过行走实验验证了软着陆控制策略的有效性[4].虽然国内外从事仿人机器人研究的机构较多,所研发的机器人多达数十种,但是这些机器人的功能大多以娱乐或服务为主[5],直接面向灾害救援仿人机器人的研究较少.众所周知,灾害救援是一项高风险、极复杂、事关人命的工作.仿人机器人要在灾害救援过程中完成稳定的行走与操作,其中下蹲取物是灾害救援工作中尤为重要的操作[6,7].所以,仿人机器人的下蹲取物动力分析对于灾害救援工作具有十分重要的意义.本文根据对仿人机器人的结构特征和下蹲取物步态的分析,将下蹲取物的仿人机器人简化为具有七自由度(重物影响)的六连杆模型,并基于拉格朗日法对其建立了便于控制的动力学方程.在设定的下蹲取物步态条件下,计算出仿人机器人各主要关节力矩时间曲线.基于合肥先进物质研究所提供的机器人全身完整的SOLIDWORK模型,导入各关节角度时间序列进行仿真模拟.通过对比分析,探讨基于拉格朗日法仿人机器人下蹲取物动力分析结果的可靠性和实用性,并为选择电机提供参考依据.
1 仿人机器人动力学模型
仿人机器人的动力学建模是一个非常复杂的过程,为了能够快速求解,必须对仿人机器人结构进行简化.对于下蹲取物而言,由于上半身腰部和整条手臂都参与运动,所以需要考虑上半身运动,因为机器人左右两部分运动对称,所以可以只考虑一边[8,9].髋关节的偏摆和肩关节的横滚影响很小,可以忽略;同时,可以认为手爪和前臂固连,脚和小腿固连并忽略头部质量[10].至此,下蹲取物可以简化为如图1所示的七自由度(重物影响)六连杆模型.
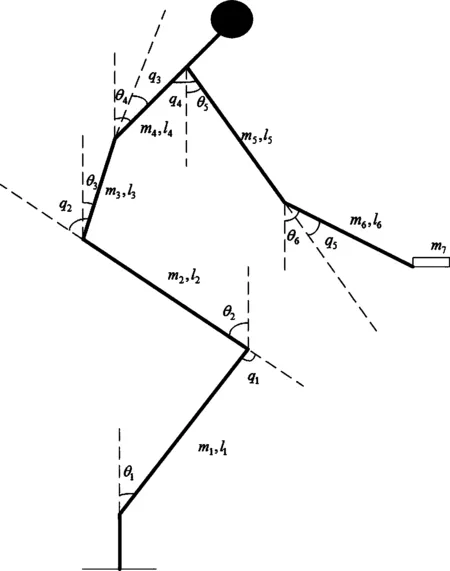
图1 下蹲取物动力学模型Fig. 1 Dynamics model of humanoid robot squatting
2 动力学方程建立与求解
关于动力学模型的求导方法,代表性的有拉格朗日方法和牛顿-欧拉方法[11-13].虽然两种方法建立的方程在本质上是等价的,但是由于方程形式不同,使得在计算和分析方面存在一定差异.针对仿人机器人的七自由度(重物影响)六连杆模型,根据拉格朗日方法建立的动力学方程形式较简洁,便于控制,计算过程的收敛性较好,计算结果可以满足工程精度要求.所以,本文将基于拉格朗日方法建立仿人机器人下蹲取物动力学方程.


(1)
动力学方程为:
(2)
这里Ti表示作用在第i个关节上的力矩.如图1,设各连杆的质量为mi,长为li,各连杆与垂直方向的夹角为θi,取顺时针方向为正.第i个杆件的质心为Gi(xi,yi).连杆下端到其质心的距离为ai,连杆绕其质心的转动惯量为Ii,与广义坐标θi对应的第i个连杆上的力矩为Ti.忽略传动转置之间的能量损耗和电机本身的转动惯量,则:

(3)
(4)
以踝关节为参考坐标系,各连杆质心的位置坐标如下:
(5)
将上面各式代入到拉格朗日动力学方程中最终整理得:
(6)
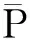
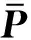
(7)
(8)
其中:Pi,j元素对称.
(9)
(10)
(11)


(12)

(13)

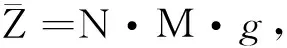
(14)
M=[m1m2m3m4m5m6m7]T,
(15)
设τ=[τ1τ2τ3τ4τ5]T为关节力矩矢量,分别代表膝关节、髋关节、腰关节、肩关节、肘关节沿y方向驱动力矩.与之对应的坐标为
q=[q1q2q3q4q5]T.
易知:
(16)
则:
(17)
T=Eτ,
(18)
式中E是关节力矩对应的坐标对系统广义坐标的雅克比矩阵的转置:

(19)
则拉格朗日方程可写为:
(20)
3 下蹲取物各关节力矩输出
由于机器人起立时才抱起重物,各关节力矩相对较大,所以只考虑取物站起过程.针对仿人机器人下蹲取物的七自由度六连杆的动力学模型,利用拉格朗日方法建立动力学方程,并利用Matlab编程求出了各主要关节的力矩时间曲线,如图2所示.
4 仿人机器人下蹲取物步态仿真
4.1 下蹲取物仿真图
本文在仿真之前已经得到了合肥先进物质研究所提供的机器人全身完整的SOLIDWORK模型,并已经添加好了各种约束和参数,所以本文将以ADAMS为基础,直接导入计算好的各关节角度时间序列进行仿真模拟,得到仿人机器人下蹲取物的仿真图,如图3所示.
4.2 关节力矩输出图
在虚拟环境中机器人脚底与地面均被设置为刚体,故在相互接触时有振动冲击,且这种振动会随时间而累加[14].体现在仿真数据上使得机器人关节力矩曲线有波动、不光滑且在抬脚与落脚瞬间各关节力矩有极大幅度的变动.为了与实际结果比较接近,对输出的关节力矩曲线进行滤波处理.对于仿人机器人下蹲取物而言,由于我们直接把重物的质量加在了手爪上,所以下蹲过程没有参考价值,我们只需要参考起立过程即7 s之后的关节力矩曲线,采用几种不同的滤波频率曲线进行比较,如图4(图中FILTERING=0.01,意为关节力矩曲线的滤波频率为0.01 Hz).
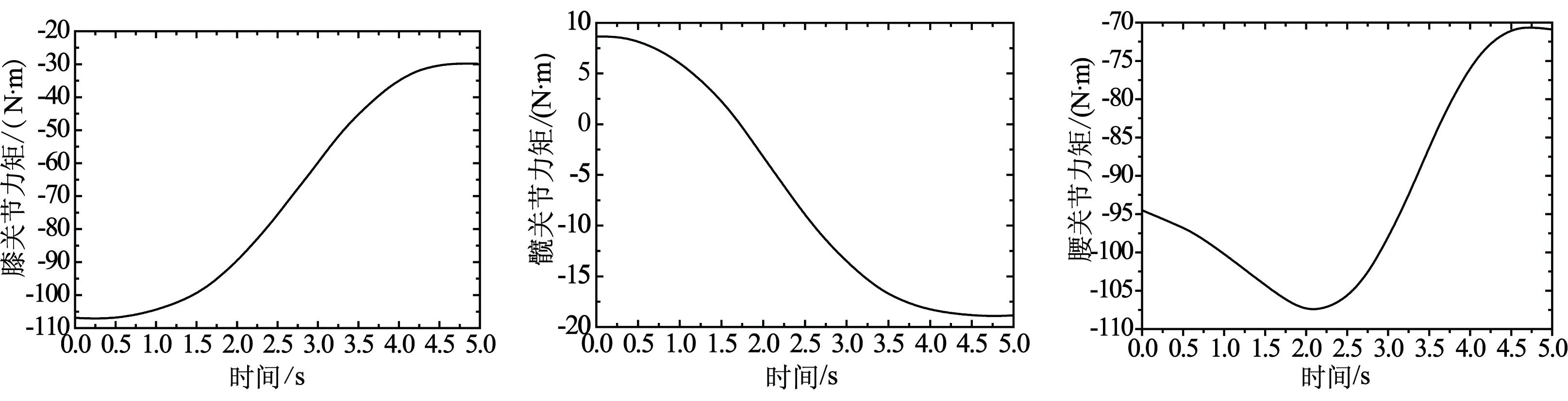
(a)膝关节 (b)髋关节 (c)腰关节
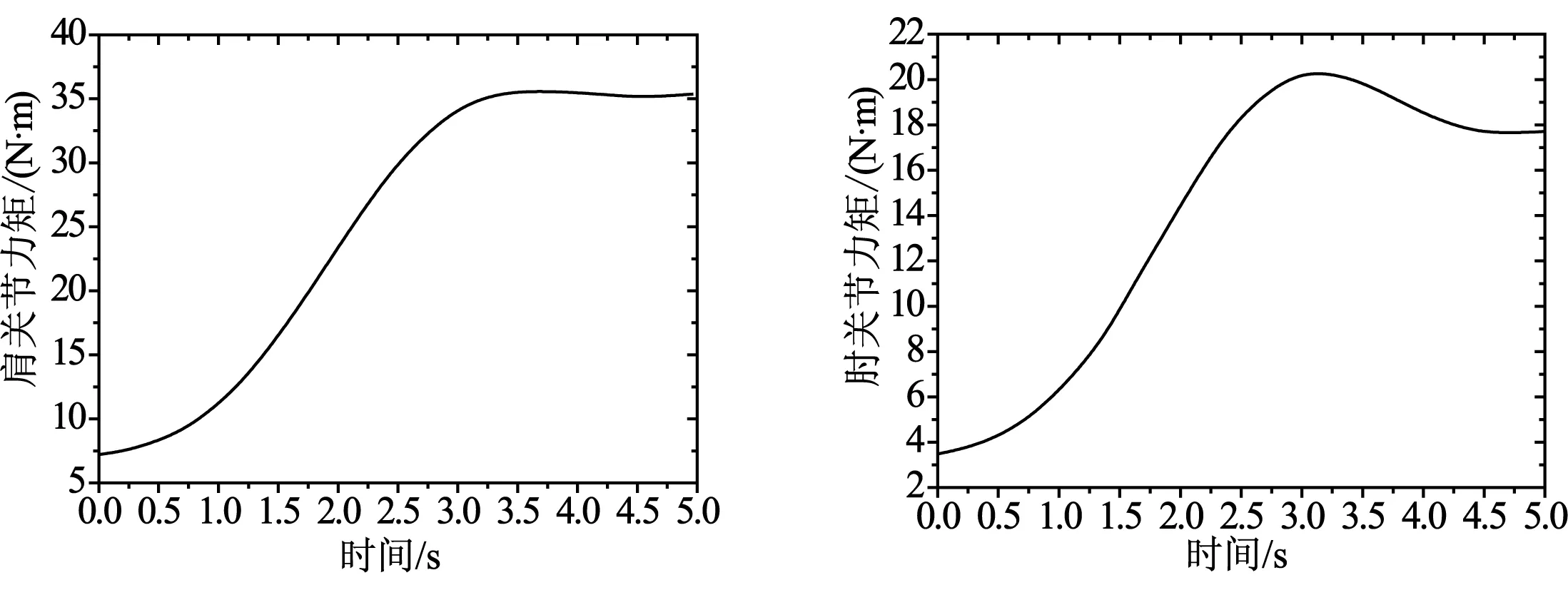
(d)肩关节 (e)肘关节

(a)下蹲过程 (b)站起过程
图4中起立过程即7 s之后的关节力矩曲线经几种不同的滤波频率处理后进行比较.由图4(a)~(e)中可知,每一关节力矩曲线采用不同频率滤波处理后,各曲线图形并不是十分吻合,但各曲线图形的峰值和谷值还是比较相近的,且与最大力矩和最小力矩的理论计算值比较接近.经对图4中(a)~(e)的分析及与理论计算的对比可知,机器人脚底与地面接触而产生振动对机器人关节力矩的影响比较大,但是最大力矩和最小力矩的理论计算值与仿真结果还是很接近.分析得到的结论可为仿人机器人工程灾害救援行为设计提供基础,也可为选择电机提供依据,并验证了基于拉格朗日法的仿人机器人下蹲取物动力分析的可靠性和实用性.

(a)膝关节俯仰方向力矩时间曲线
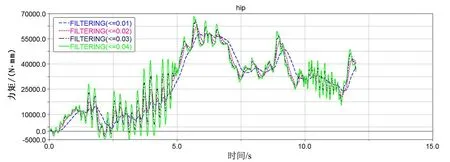
(b)髋关节俯仰方向力矩时间曲线

(c)腰关节俯仰方向力矩时间曲线

(d)肩关节俯仰方向力矩时间曲线
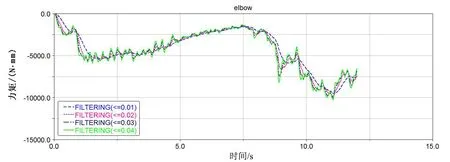
(e)肘关节俯仰方向力矩时间曲线
5 结论
本文将工程灾害救援环境下仿人机器人下蹲取物简化为具有七自由度(重物影响)的六连杆模型,基于拉格朗日法对其建立了便于控制的动力学方程,进而计算出各主要关节力矩时间曲线,并揭示了工程灾害救援环境下仿人机器人下蹲取物主要关节的受力机理,从而为仿人机器人的救援行为设计提供了基础.
