双向循环荷载作用下饱和红土的动变形强度特性
2018-08-10骆亚生
徐 鹏,骆亚生,李 焱,2
(1 西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100;2 江西省水利科学研究院,江西 南昌 330029)
地震灾害在世界各地时有发生,地震荷载作用下土体会发生软化、破坏、震陷现象,使地表建筑物或道路因变形过大而造成人员伤亡和经济损失,所以动荷载作用下土体的动力特性一直是土动力学研究的重要内容[1]。当地震发生时,从震源处激发出横波和纵波向地面传播,横波(S波)产生剪切动荷载,纵波(P波)产生拉压动荷载。由于纵波在土体传播过程中衰减速度较快,对于震级较小或震源较深的地震而言,纵波传播到地表时动加速度已经衰减至很小,因此对土体作用甚微[2-3]。基于上述理论Seed等[4-6]提出将地震荷载简化为一水平剪切动荷载的方法,即忽略纵波及其与横波叠加产生的面波(瑞利波和勒夫波)的影响。但在近场地震中,由于震源距离地面近、纵波传播速度快,当其传播至地面时仍有较大的动加速度,并不能衰减完全,此时在研究中忽略纵波的影响是不合理的,在抗震设计中也是偏于不安全的。近年来国内外的一些震害资料表明,发生在城市附近的直下型地震,尤其是震源深度较小的近场地震,许多建筑物都因竖向开裂而破坏[7-9],如1976年的唐山大地震、1985年的墨西哥地震和1995年的日本阪神地震等,均表明纵波影响较大。因此,在对土体进行动力特性研究时,能同时考虑横波的剪切作用和纵波的拉压作用,研究结果可以更加接近地震时的实际情况。国内外学者在轴向拉压荷载及其与扭转剪切荷载耦合作用对土体动力特性的影响方面已经进行了大量研究[10-16],但是关于轴向和径向拉压荷载耦合作用对土体动力特性的影响研究还比较少见。Rascol[17]通过分析拉压和剪切荷载耦合作用对饱和砂土液化特性影响得出,在某些情况下耦合作用加快了砂土液化。国内学者在对饱和软黏土双向激振循环荷载的试验中发现,径向循环应力对土体的动力特性有较大影响[18-22]。如蔡袁强等[18]在双向激振循环荷载对饱和软黏土强度和变形特性影响的研究中得到,随着径向循环应力比的增加,循环应变幅增加速度加快,强度降低,孔压幅值增大。
红土是一种特殊工程地质性质土体,主要分布于热带、亚热带湿热地区,面积约为200万km2[23-24]。我国长江以南地区红土广泛分布,该地区地震频发且多为近场地震,如1999年台湾集集地震、2005年江西九江瑞昌地震、2008年四川汶川地震等。所以在拉压和剪切动荷载双向耦合作用下开展红土动力特性研究就显得十分必要,其结果将对该地区防灾减灾、工程抗震设计具有一定的指导意义,但目前尚少有学者研究红土的动力特性。鉴于此,本试验以江西红土为例,在双向循环荷载耦合条件下研究径向循环荷载幅值和相位差变化对饱和红土动变形发展及动强度的影响,以期为红土动力特性研究提供一定的理论支持。
1 材料与方法
1.1 试验材料
试验中使用的仪器为SDT-20型电脑控制电液伺服双向土动三轴试验机,仪器轴向振动的动态负荷可达±20 kN,轴向静变形控制速率为0.01~5 mm/min,三轴压力室的承压值为0~1 MPa,液压源流量30 L/min,最大压力为21 MPa。
试验所用土样取自江西省东乡县第二中学新校区工地周边,取土深度3~4 m,天然干密度为1.47 g/cm3,用酒精燃烧法测得天然含水率为19.6%,通过标准击实试验测得最大干密度为1.67 g/cm3,最优含水率为19.8%,根据塑性土分类为低液限黏土。试验土样的基本物理性质如表1所示。

表1 试验土样的物理性质指标Table 1 Physical properties of soil samples
试验采用重塑试样,干密度为1.59 g/cm3,试样直径39.1 mm,高度为80 mm。用制样器制得试样后,将试样装入饱和器在抽真空饱和仪中先抽真空1 h,再慢慢浸水,继续抽真空1 h,静置24 h后备用,试验前对孔隙水压力和侧向压力的比值即孔隙水压力系数(B)进行测定,当B≤0.95时需要进行反压饱和,直至B>0.95认为试样达到饱和,测得饱和试样含水率为25.5%。
1.2 试验方法
1.2.1 应力路径确定 不同应力路径下土体的变形特性不同[25]。在双向动三轴试验中,当循环偏应力幅值或轴向循环应力幅值为定值时,不同的径向循环应力幅值可以形成不同的应力路径,依据谷川[7]的研究结果,定义应力路径斜率ηdm为:
ηdm=pdm/qdm。
(1)
式中:pdm为循环平均主应力幅值,qdm为循环偏应力幅值。
在相位差φ=0°和φ=180°时应力路径均为一直线,应力路径斜率可以用来表征不同的应力路径。
当φ=0°时,有:
qdm=σdvm-σdhm,
(2)
pdm=(σdvm+2σdhm)/3。
(3)
当φ=180°时,有:
qdm=σdvm+σdhm,
(4)
pdm=(σdvm-2σdhm)/3。
(5)
式中:σdvm和σdhm分别为轴向和径向循环应力幅值。
当ηdm=0.33时表示只有轴向循环荷载作用下的单向动三轴试验,由上式可知,φ=0°时,ηdm>0.33;φ=180°时,ηdm<0.33。图1为φ=0°或φ=180°时,不同斜率下的应力路径。

图1 循环应力作用下的应力路径示意图(φ=0°或φ=180°)Fig.1 Stress paths under cyclic stress (φ=0° or φ=180°)
1.2.2 试验方案 本研究共进行2组试验:第1组试验为饱和红土动强度试验,即在围压σ3c为200 kPa,σdhm分别为20,40 kPa,φ分别为0°,45°,90°,135°,180°,225°,270°和315°的条件下,给定3个适当的轴向循环应力幅值,使3个试样的破坏振次分别在1~10,10~100,100~1 000,以研究相位差对饱和红土动强度的影响。第2组试验为饱和红土动变形试验,试验分为3部分:第一,在轴向、径向循环应力幅值为定值(σdhm=20 kPa,σdvm=87.5 kPa)时,探究相位差(φ=0°,45°,90°,135°,180°,225°,270°,315°)对饱和红土动变形的影响;第二,在φ=0°条件下,考虑不同围压(σ3c=100,200 kPa)下循环偏应力幅值为定值(qdm=50,67.5 kPa)时,探究ηdm对饱和红土动变形的影响;第三,同一围压σ3c=100 kPa下考虑轴向循环应力幅值为定值(σdvm=83.3,50 kPa),径向循环应力幅值σdhm为0,20,40,60 kPa时,在φ=0°和φ=180°的2种情况下,探究ηdm对饱和红土动变形的影响。为更好地体现变量间的相互关系,本研究对循环振动次数取对数在半对数坐标系中制图。
采用固结不排水方式进行试验,试验均采用一级加载方式进行加载,整个试验过程中轴向、径向循环应力幅值一直保持不变,直至试样的轴向应变达到5%时,认为试样被破坏。在试验过程中,先保持固结围压不变对试样进行均压固结,30 min内待试样轴向变形小于0.01 mm时,认为试样固结稳定。固结完成后对试样进行双向激振,轴向和侧向均为简谐荷载,频率为1 Hz。
因为45°剪切面上同时存在剪应力和正应力,可以很好地反映剪切动荷载与拉压动荷载耦合情况下引起的饱和红土动变形和动强度变化规律,所以对45°剪切面上受力情况来进行分析,以其动剪应力幅值(τdm)来体现土体的动强度。在均压固结条件下,双向振动三轴试验可以看作是由固结围压与双向循环荷载两部分荷载耦合下的共同作用,试样上的应力如图2所示。图2中,σc和τc分别为均压固结下45°剪切面上的正应力和剪应力,σ1c和σ3c分别为轴向和径向固结围压,σd和τd分别为双向循环荷载在任意相位差耦合下45°剪切面上的任意时刻的动正应力和动剪应力,σp和τp分别为均压固结荷载与双向循环荷载在任意相位差耦合下45°剪切面上任意时刻的耦合正应力和耦合剪切应力。由图2可以分别得出均压固结作用和双向循环荷载作用下45°剪切面上任意时刻的正应力与剪应力。

图2 双向循环荷载作用下试样应力示意图Fig.2 Stress diagram of sample under bidirectional cyclic loads
对均压固结作用,有:
(6)
(7)
对双向循环荷载作用,有:
(8)
(9)
由上述2种情况下对应的应力叠加可以得到45°剪切面上任意时刻的耦合正应力σp与耦合剪切应力τp,即:
σp=σc+σd=σ3c+σdmsin (2πt+θ),
(10)
τp=τc+τd=τd。
(11)
式中:σdm、τdm分别为双向循环荷载作用下45°剪切面上动正应力幅值和动剪应力幅值,θ为与φ相关的角。
3 结果与分析
3.1 应力路径斜率对饱和红土轴向应变的影响
在动三轴试验中,对土体变形的研究多以轴向应变ε为主要研究对象,图3所示为相位差相同、ηdm不同时,轴向应变与循环振动次数的关系曲线,其中图3-a、b分别为σ3c在100 kPa下,轴向循环应力幅值(σdvm)为定值,φ=0°,180°时ηdm变化对轴向应变发展速度的影响。
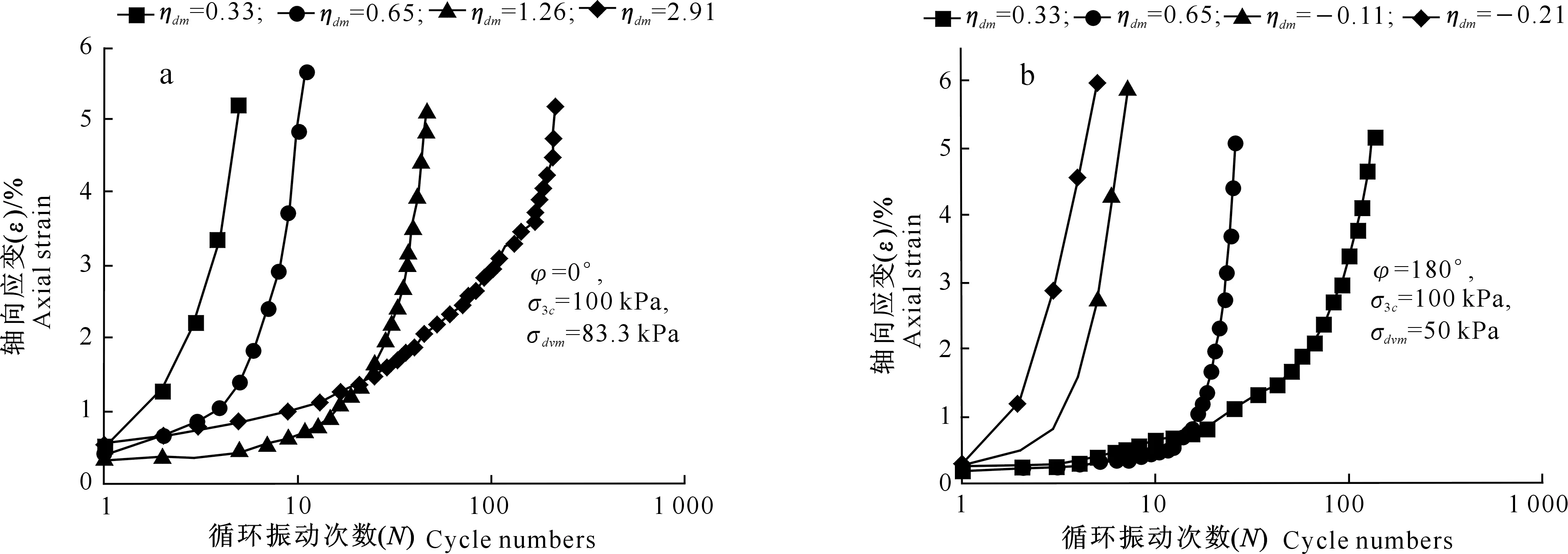
图3 轴向循环应力幅值(σdvm)为定值时饱和红土轴向应变与循环振动次数关系曲线Fig.3 Relationship between axial strain and cycle numbers of saturated laterite when axial cyclic stress amplitude (σdvm) is determined
由图3可以看出,在φ=0°和φ=180°时,轴向应变随循环振动次数的增加其发展速度均越来越快,且两者动应变随ηdm变化的发展规律基本相同。在φ=0°时,ηdm越大达到相同应变所需循环振动次数也越大,这就说明不同的应力路径影响土体的变形速度,ηdm越大,即径向循环应力幅值越大,对应应力路径下土体动应变的发展速度越缓慢。在φ=180°时,这种变化趋势完全相同。两种情况都说明径向循环应力幅值对土体动应变的影响不可忽略。
图4表示同一φ不同ηdm条件下,当循环偏应力幅值(qdm)为定值时,轴向应变与循环振动次数的关系曲线。由图4可见,当循环偏应力幅值一定时,应力路径斜率ηdm越大,轴向应变发展越缓慢。当φ=0°时,与单向振动(ηdm=0.33)相比,图3、4均表明径向循环应力幅值的存在减缓了土体轴向应变的发展,且不同围压条件下表现出了相同的变化规律。
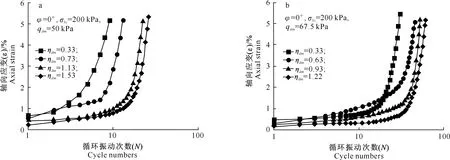
图4 循环偏应力幅值(qdm)为定值时饱和红土轴向应变与循环振动次数关系曲线Fig.4 Relationship between axial strain and cycle numbers of saturated laterite when cyclic deviatorics stress amplitude (qdm) is determined
3.2 相位差对饱和红土轴向应变的影响
当σ3c=200 kPa、σdhm=20 kPa、σdvm=87.5 kPa时,不同φ下轴向应变与循环振动次数关系见图5。
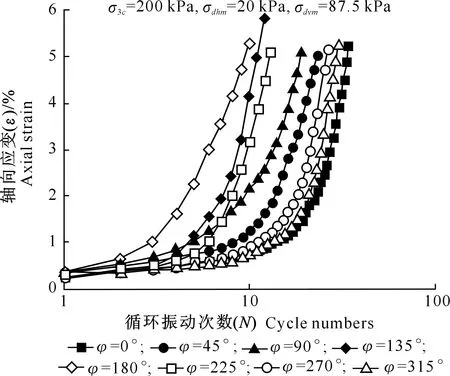
图5 不同相位差下饱和红土轴向应变与循环振动次数关系曲线Fig.5 Relationship between axial strain and cycle numbers of saturated laterite under different phase differences
由图5可见,当φ=0°~180°时,轴向应变发展速度随φ的增加而增大;而φ=180°~360°时,轴向应变发展速度变化规律则相反,即轴向应变随φ增大而减小。φ=0°时轴向应变发展速度最慢,φ=180°时轴向应变发展速度最快,其他相位差的轴向应变发展速度介于两者之间。
3.3 相位差对饱和红土动强度的影响
由图6可以看出,同一循环振动次数下,随φ增大动强度以180°为转折点先减小后增大,φ=0°时动强度最大,φ=180°时动强度最小。地震中,横波和纵波之间的相位差可能是任意大小,但是φ=180°情况下土体动强度最小,对土体稳定最为不利。
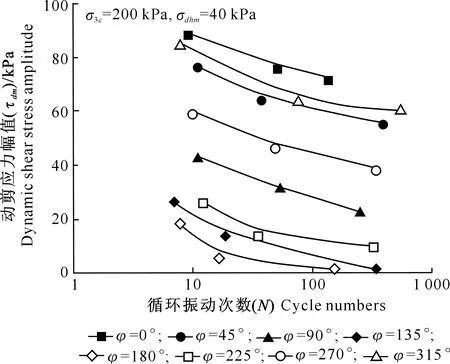
图6 不同相位差下饱和红土的动强度曲线Fig.6 Dynamic strength of saturated laterite under different phase differences
图7为围压σ3c=200 kPa条件下,径向循环应力幅值σdhm=20和40 kPa,循环振动次数为20时,对应的动剪应力幅值τdm随相位差φ变化的关系曲线。图7中,τdm基本上关于φ=180°呈轴对称分布,相同φ下,σdhm=40 kPa时土体的τdm均小于σdhm=20 kPa时。
由图7还可以看出,σdhm=40 kPa、φ=180°时荷载组合下土体τdm最低,也是对土体稳定最为不利的组合,此种组合下的τdm分别是σdhm=20 kPa、φ=180°组合以及σdhm=40 kPa、φ=0°组合的14.4%和9.2%。τdm在不同相位差φ和径向循环荷载幅σdhm组合情况下衰减率最高可以达到90%以上,因此相位差和径向循环荷载幅值大小对土体动力特性的影响不可忽略,在实际工程的抗震设计时,应充分考虑双向动荷载相位差为180°及此时径向动荷载幅值较大的组合情况。

图7 饱和红土动剪应力幅值(τdm)与相位差(φ)的关系曲线Fig.7 Relationship between dynamic shear stress amplitude (τdm) and (φ) phase difference of saturated laterite
3.4 原因分析
将试验中不同的相位差和循环荷载幅值代入式(8)、(9),并结合图3、4、5进行分析,可以得出双向循环荷载幅值作用下45°剪切面上σdm与τdm以及ε的变化情况:当φ在0°~180°范围内增大时,σdm逐渐减小,而τdm逐渐增大,ε发展加快;当φ在180°~360°范围内增大时,σdm逐渐增大,τdm逐渐减小,ε发展减慢。在φ=0°条件下,当σdvm为定值时,随着σdhm的增大,σdm逐渐增大,τdm逐渐减小,ε发展减慢;当qdm为定值时,随着σdhm的增大,σdm逐渐增大,τdm不变,ε发展减慢。
因为本试验所施加的动应力均小于试样所受的固结围压,所以由式(10)可以看出,任意时刻的耦合正应力σp始终为正值,其方向垂直于45°剪切面向内,所以45°剪切面上土体始终处于受压状态。φ在0°~360°内增大时,45°剪切面上土体承受的动剪应力幅值τdm先增大后减小,φ为180°时τdm最大且此时耦合正应力σp最小,所以φ=180°时的动应变发展速度最快,表现出的动强度最小。随着φ的增大,动正应力幅值σdm和动剪应力幅值τdm同时变化,但ε发展与τdm的变化趋势一致,总是随着τdm的增大而加快,随τdm减小而减慢,说明动剪应力对土体动变形发展的影响更为显著。随着σdhm的增大,在φ=0°时,τdm减小或不变时,ε总是随着σdm的增大而发展减慢,说明拉压动荷载的存在对土体动变形发展有不可忽略的影响,此种情况下其存在减缓了土体动变形的发展。
4 结 论
通过对饱和红土试样同时施加轴向和径向循环荷载,探究不同应力路径下试样的动变形和动强度特性,得出以下结论:
1)在φ=0°和φ=180°时,应力路径斜率变化对饱和红土轴向动应变的影响规律完全相同,即应力路径斜率越大,轴向动应变发展速度越缓慢。
2)相位差对饱和红土的轴向动变形有明显影响。当φ在0°~180°范围增大时,轴向应变发展速度越来越快;当φ在180°~360°范围增大时,轴向应变发展速度却越来越缓慢。
3)相位差对饱和红土的动强度影响显著。随φ增大,τdm以φ=180°为转折点呈先减小后增大趋势,基本上关于φ=180°呈对称分布。在最不利组合情况下,τdm衰减率可以达到90%以上。
4)拉压循环荷载的作用在一定条件下减缓土体动变形发展,在拉压循环荷载和剪切循环荷载耦合条件下,剪切循环荷载对土体动变形的影响更为显著。
