基于数学期望的风向和风速对农田防护林网防风效能的影响

张 帅，丁国栋*，高广磊，赵媛媛，包岩峰，于明含

(1.北京林业大学水土保持国家林业局重点实验室，北京 100083；2.北京林业大学 水土保持学院，宁夏盐池毛乌素沙地生态系统国家定位观测研究站，北京 100083；3.中国林业科学研究院荒漠化研究所，北京 100091)

土壤风蚀是指在以风力为主要外营力的作用下导致地表物质分散的物理过程，是造成环境恶化和土地生产力下降的主要原因之一[1-2].农田防护林作为生态建设的重要工程措施，能有效改善生产生活环境和局地小气候，防止地表风蚀，减轻风沙危害，为生态安全提供保障[3-4].我国在很早之前就开始了防护林的营造，并在防护林建设等方面做了大量工作[5-6].目前防护林体系发展完善，空间格局多样，可针对不同的保护对象设置相应的林网配置模式[7].防护林的防护作用主要表现在防风效能上[8-10]，风速的降低可引起其他气象要素的改变，进而调节微气候环境[11-13].现有研究通过野外观测及风洞模拟的方法对影响农田防护林防风效能的因素进行了大量实验[14-17]，并借助数学模型在细碎化、景观结构方面进行评价，分析了林带宽度、高度、结构类型、疏透度等对防护林防风效能的影响[18-21].但现有研究大多建立在主害风向与主林带垂直的前提下，而在实践中发现，由于地形的限制，防护林的营造常会出现与主害风向不垂直的情况，且部分地区气候变化较大，主害风向会出现较大差异，因此，仅分析垂直主林带风向的防风效能并不能反应真实状况.针对这一问题，本研究通过数学期望的方法，对不同风向的林网内风速及防风效能进行综合分析，以期揭示农田防护林网对旷野风速运动变化所产生的作用和影响，为农田防护林的规划提供依据.

1 研究区概况

研究区位于乌兰布和沙漠东北缘中国林业科学研究院沙漠林业实验中心(以下简称沙林中心)第三实验场，行政区划属于内蒙古自治区磴口县.研究区处于温带干旱区，东临黄河，为黄河冲积平原，属温带大陆性气候.年平均降水量为144.5 mm，降水量分配不均，集中分布在6—9月，占全年降水量的78%；年平均蒸发量为2 397.6 mm，年平均湿润系数为0.094；年平均日照总时长为3 209.5 h，年均10 ℃及以上有效积温为3 100～3 400 ℃，年无霜期为140～160 d；年平均风速为3.0～3.7 m/s，年大风日数为20～40 d.

研究区雨热同期，且具有引黄灌溉的条件.植被类型丰富，试验地为独立防护林网，主要造林树种为新疆杨(PopulusalbaL. var.pyramidalisBunge)，树龄为24 a，长势良好.主林带间距140 m，副林带间距300 m，无明显缺口，基本情况详见表1.

表1 试验农田防护林网概况

Tab.1 General situation of farmland shelterbelt networks

林带株行距/m树高/m枝下高/m冠幅/m胸径/m走向主林带a1.0×1.524.03.03.1×3.827.5南北主林带b1.0×1.522.51.92.7×4.020.5南北副林带a1.0×2.023.32.83.0×2.224.3东西副林带b1.0×2.025.54.34.2×2.426.0东西

注：根据主害风向，林网西侧、东侧林带分别定义为主林带a和主林带b，北侧和南侧林带分别定义为副林带a和副林带b.

2 观测点布设与观测方法

2.1 观测点布设

防护林网内的观测点布设情况如图1所示：设定林网中心为原点，副林带方向以平均树高(h)为间距向两侧布设观测点，共布设5列；主林带方向以2h为间距向两侧布设观测点，共布设5行.林网内总计观测点为25个.

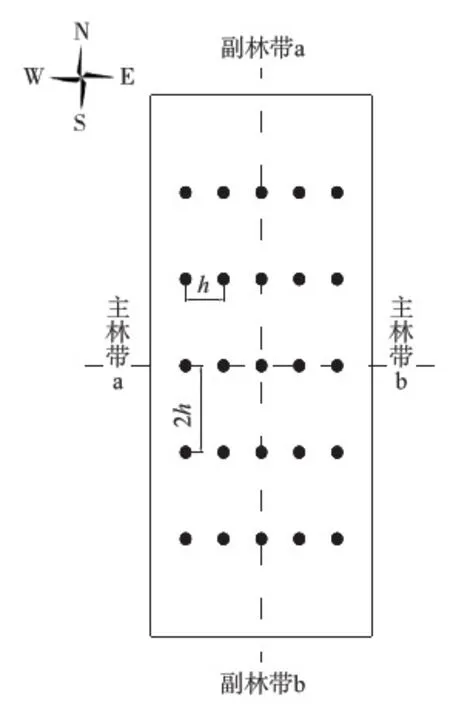
图1 防护林网内观测点示意图Fig.1 A schematic diagram of the observation sites in shelterbelt networks

2.2 风速测定

在防护林内按照图1所示观测点布设三杯风速传感器(S-WSA-M003)，并连接HOBO-U30-NRC数据采集器，数据测定间隔设置为1 s，观测高度为距地面2 m[19]，同时以沙林中心沙地地面气象站便携式气象参数综合测试仪(LS2009)观测数据作为旷野对照风速.

2.3 气象资料

检索磴口区站2005—2015年间的气象资料，按照图2所示对风向进行分区，统计不同风向出现的频数，并计算其频率，作为计算防护林防风效能数学期望值的依据.所用数据来源于中国气象科学数据共享服务网(http：∥data.cma.cn/).

2.4 防风效能

采用下式计算防风效能exz，用以表示风速减弱的程度：

式中，u0z表示高度z处的旷野对照风速，uxz表示防护林网内主林带背风侧距林带x、高度z处的平均风速.

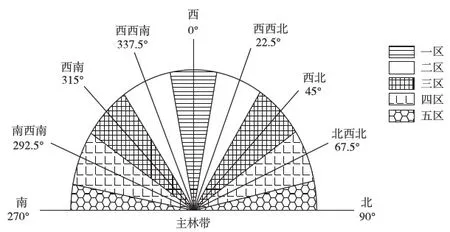
图2 风向分区示意图Fig.2 A schematic diagram of the wind direction partitions

2.5 数学期望

采用下式计算防风效能的数学期望Exz：

式中，exzi表示防护林网内主林带背风侧距林带x、高度z、风向i时的防风效能，pi表示风向i出现的频率.

2.6 数据处理方法

基于样本观测值统计平均值、标准差、极值、变异系数等，计算样本频数分布，并对样本数据进行单变量方差分析，比较风速差异.运用地统计学方法拟合风速变异函数，分析空间异质性和空间自相关性，并选取平均风速值在Surfer 13.0软件中利用克里金(Kriging)插值法绘制等值线图，分析林网内风速分布状况.

3 结果与分析

3.1 风向对林网内平均风速的影响

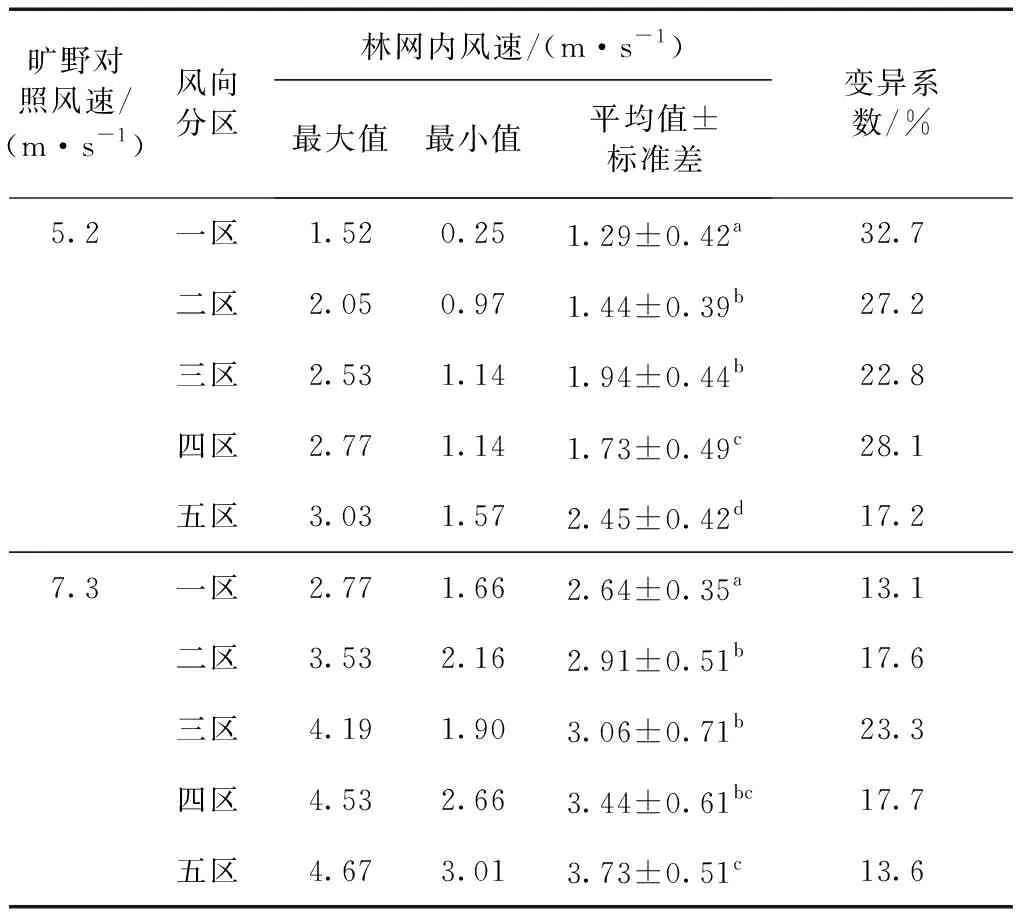
防护林网内风速的统计分析结果如表2所示，可以看出风向对防护林网内风速影响较明显，随着风向与主林带夹角的减小，平均风速呈现出增大的趋势.不同风速下各风向的最大值均小于旷野对照风速，表明防护林网发挥了防风作用，一至五区不同风速的平均防风效能分别达到69.5%，66.2%，60.4%，59.8%和50.1%.单变量方差分析结果显示，风向为五区时防护林网内风速的变异系数较小，其他风区平均风速差异显著(p<0.05)，这是由于当风向与主林带夹角较大时，气流能更顺畅地通过林带间隙，更容易形成狭管效应及涡流，导致林网内气流变化复杂，风速数值波动明显，造成样本间差异较大.

表2 防护林网内风速统计特征

Tab.2 Characteristics of wind speed statistics in shelterbelt networks

旷野对照风速/(m·s-1)风向分区林网内风速/(m·s-1)最大值最小值平均值±标准差变异系数/%5.2一区1.520.251.29±0.42a32.7二区2.050.971.44±0.39b27.2三区2.531.141.94±0.44b22.8四区2.771.141.73±0.49c28.1五区3.031.572.45±0.42d17.27.3一区2.771.662.64±0.35a13.1二区3.532.162.91±0.51b17.6三区4.191.903.06±0.71b23.3四区4.532.663.44±0.61bc17.7五区4.673.013.73±0.51c13.6

注：不同小写字母表示在p=0.05水平上差异显著.

统计不同风区防护林网内风速频数的正态分布概率，结果如图3所示.可以看出：风向在一区时风速频数分布较均匀，不符合正态分布，没有明显的偏度；风向在二区时风速频数属于正态分布中短尾分布，区间数据具有正偏离态势；风向在三区低风速、四区不同风速及五区高风速时风速频数属于左偏态分布，区间数据具有正偏离态势；风向在三区高风速及五区低风速时风速频数属于长尾分布，区间数据具有负偏离态势.由此可见，不同风向的风速频数分布差异较大，没有明显的规律性，进一步说明风速频数的变异系数较大，样本数据差异不显著.

3.2 不同风向频率

统计研究区2005—2015年间的气象资料发现，一至五区风向出现的频率分别为3.31%，55.25%，22.10%，11.05%和8.29%.主害风向与主林带角度较大的一区和二区风向出现的总频率为58.56%，表明研究区当地林带走向设置不合理，防护林不能充分发挥其防风作用.

图3 防护林网内不同风区风速频数的正态分布概率Fig.3 Normal frequency probabilities of wind speed in different partitions in shelterbelt networks

3.3 风向对林网内风速空间异质性的影响

利用地统计学的方法，分析不同风速下防护林网内风速的空间异质性，对其变异函数进行拟合并计算其参数，结果如图4所示：当风速为5.2 m/s时，防护林带内平均风速数学期望值可以较好地拟合为指数函数；当风速为7.3 m/s时，则选用高斯函数对防护林带内平均风速数学期望值具有更高的拟合度.

图4 平均风速数学期望值半方差分析Fig.4 Semi-variance analysis of mean wind velocity mathematical expectation

表3 防护林网内风速变异函数参数

Tab.3 Parameters of the variation function of wind velocity in shelterbelt networks

旷野风速/(m·s-1)模型C0C+C0空间相关度/%AR2RSS/10-45.2指数函数0.000 10.086 70.1092.90.8312.667.3高斯函数0.000 10.234 20.1070.80.9853.52

从表3中可以看出：块金值(C0)较小，与基台值(C+C0)的比值(空间相关度)远小于强烈空间相关度的标准25%，表明样本具有较强的空间自相关性，对其进行插值模拟具有准确性；变异函数的变程(A)分别为92.9和70.8，均远大于观测点间距(2h)，表明样本取样连续性强，且取样间隔较为合理；两个变异函数模型的决定系数(R2)较高，残差(RSS)较小，表明模型的选择较为合适.

3.4 防风效能数学期望值分布

计算防风效能数学期望值，并利用克里金插值法模拟出防风效能图，如图5所示，防护林在不同风速下均发挥较强的防护作用，防风效能最小值均大于0.5；不同风速下防风效能图结构特征相似，在林网中间区域防护效果较差，主林带和副林带交界的区域防护效果较好.当风速为5.2 m/s时，林带南侧0～75 m区域内风速较小，形成明显的风影区，最高防风效能达到0.79；林网内距副林带100～200 m范围内是低防风效能区，在此区域内等值线较为密集，表明风速变化较剧烈，气流稳定性差，沿风向自西向东风速先上升后下降，最低防风效能为0.58；林带北侧0～75 m范围内等值线稀疏，气流较稳定，且防风效能变化幅度较小，形成稳定风速区域.当风速为7.3 m/s时，防护林网内西南区域和东北区域形成明显的防风效能区；中间区域由西北向东南形成近似菱形低防风效能区，在此区域内等值线较为稀疏，表明该区域虽保持较高的风速，但气流较为稳定，此时最低防风效能为0.5.当风速增大时，防护林网内防风效能区面积增大，但整体防护效果降低，表明防护林在低风速时能发挥更好的防护效果.

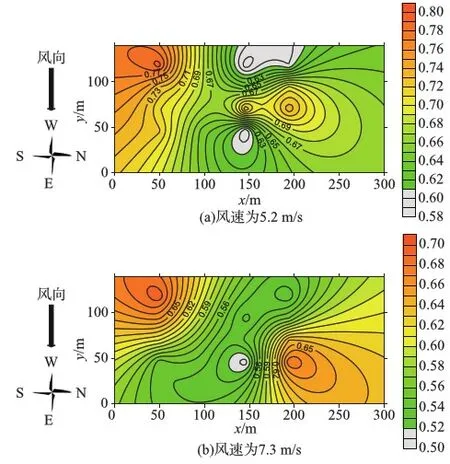
图5 不同风速条件下防护林网内防风效能模拟Fig.5 Simulation of windbreak efficiency in shelterbelt networks under different wind speeds

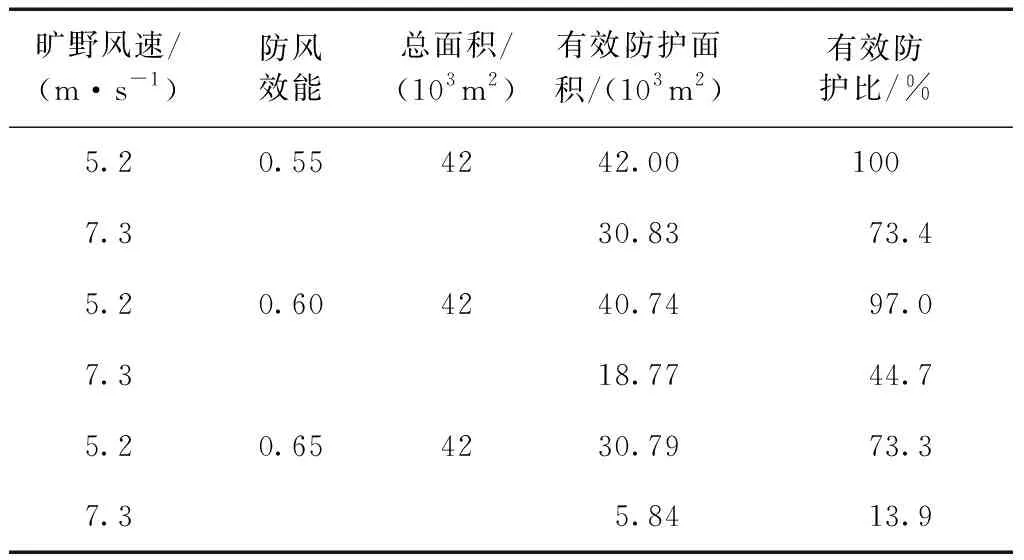
防风效能图可以直观地展现林网内风速区域的划分和差异性，但不能定量分析不同风速下林网防护范围的大小，为此引入有效防护面积的概念.根据防风效能图中等值线的插值模拟，确定不同标准下林网内的有效防护面积，结果如表4所示.当风速为5.2 m/s时，防护林防护作用较强，林网内均能达到0.55的防风效能；当风速增大至7.3 m/s时，有效防护比下降至73.4%，有效防护面积随风速的增大而减小，这是由于风速增大时，动能以几何倍数增长，单一防护林网不能完全吸收动能.当把防风效能标准提高到0.60时，与防风效能为0.55时相比，低风速下林网内有效防护比下降了3个百分点，而高风速下林网内有效防护比急剧下降了28.7个百分点，此时低风速下的有效防护面积是高风速下的2.17倍.当继续把防风效能标准提高到0.65时，与防风效能为0.60时相比，低风速下林网内有效防护比下降了23.7个百分点，而高风速下林网内有效防护比下降了30.8个百分点，

表4 不同风速下防护林网内有效防护面积

Tab.4 Effective protection area of shelterbetl networks under different wind speeds

旷野风速/(m·s-1)防风效能总面积/(103m2)有效防护面积/(103m2)有效防护比/%5.20.554242.001007.330.8373.45.20.604240.7497.07.318.7744.75.20.654230.7973.37.35.8413.9

此时低风速下的有效防护面积为高风速下的5.27倍.上述结果表明，防护林网能发挥较强的防护作用，但随着风速的增大，有效防护面积呈现减小的趋势.

4 讨 论

在进行防风效能的模拟中，控制点的数量越多，模拟结果越准确；但在实践中，由于受到实验仪器及环境因素的影响，控制点的数量经常受到限制.控制点布设的合理性可运用变异函数来判断.变异函数是地统计学中常用的手段和工具，用来研究区域化变量空间变化特征和强度，也被定义为区域化变量增量平方的数学期望[22].变程表示区域化变量从存在空间相关状态转到不存在空间相关状态的临界点，其值反映该变量的空间自相关范围的大小，即空间自相关尺度，一般认为变程大于样本间隔时，样本空间存在自相关性.在本研究中，高、低风速条件下变程分别为70.8和92.9，均大于最大观测点间距(2h)，因此可认为观测点布设合理，模拟效果准确.

通过分析磴口区站气象资料可以看到，与主林带夹角较大的风向出现频率是58.56%，与主林带夹角较小的风向出现的频率为41.44%，表明本研究区防护林的布置并未充分发挥其防护作用，主林带走向与二、三区风向垂直可产生更好的防护效果.本研究中防风效能图的控制点数据是基于数学期望计算所得，是所有防风效能的综合，与范志平等[3]的单次风速分布图结构有较大的差异；同时，风速变异函数模型选取与吕仁猛[9]的球状模型不同，但自相关程度高，变程合理，决定系数较大，仍具有强烈的空间相关性及样本区间的合理性.

风向与主林带垂直时，除上风向林带的阻滞减速作用外，会在林网中心形成较大的涡流减速区，随后风速增大，中心涡流减速区风速数值明显低于林网内其他区域；当风向为二区的角度时，林网的中心涡流减速区面积减小，且风速数值与林带后减速区风速差异较小；当风向为三区的角度时，林网内仅在上风向主林带与副林带相交的区域出现小面积的减速区，林网中心涡流减速区消失；当风向为四区的角度时，林网内流场结构与三区相似，但风速恢复区的风速数值有了明显提高；当风向为五区的角度时，上风向副林带后形成阻滞减速区，范围约占林带的1/4，随后在林网内形成较大面积的加速区，整个林网内风速数值均有了较明显的提升.由此可见，风向与主林带夹角变小时，防护林防护作用的减小表现为减速区域面积的减小和防风效能减弱导致风速数值的上升.

5 结 论

不同风速条件下防护林网空间相关度均为0.10%，具有较强的空间自相关性，高、低风速可分别较好地拟合为高斯函数和指数函数，变程分别为70.8和92.9，均高于最大取样间隔，插值模拟具有较强的可靠性，风速样本数据变异系数较大，离散程度较高，并不完全符合正态分布.防护林网对不同风向的风均有较强的防护作用，风向从一至五区的平均防风效能分别达到69.5%，66.2%，60.4%，59.8%和50.1%，但随着风速的增大有效防护比呈现出降低的趋势，风速为5.2 m/s时平均有效防护面积为90.1%，当风速增大到7.3 m/s时平均有效防护面积下降至44.0%.本研究基于风向数学期望的防风效能展现出林网对不同风向防护效果的差异，弥补了单一风向防风效能实践性和准确性较差的缺陷，能充分表明防护林网的综合防护效益，对防护林的建设具有一定的指导作用.