基于多元聚类模型与两阶段聚类修正算法的变电站特性分析
2018-08-09蒋正邦孙维真商佳宜
蒋正邦, 吴 浩, 程 祥, 孙维真, 商佳宜
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 国网浙江省电力有限公司杭州供电公司, 浙江省杭州市 310011; 3. 浙江电力调度通信中心, 浙江省杭州市 310007)
0 引言
在智能电网的大环境下,电力公司用电信息采集系统、电力营销系统和客户服务信息系统等积累了有关用户与变电站的海量用电信息[1]。充分挖掘与分析这些信息中所蕴含的变电站共性特征,对变电站建模、指导合理用电及安排供电规划、高效利用能源等方面具有重要意义[2-3]。目前,聚类分析是对变电站用电信息进行数据挖掘的重要方法之一。
对变电站聚类分析的研究途径主要有两种,一种是针对变电站的用户构成对变电站进行聚类,另一种是针对变电站的日负荷曲线对变电站进行聚类[4-7]。用户构成一般指变电站中各类用户所占的比例,采用用户构成作为聚类指标的研究者认为,用户构成是造成综合负荷特性差异的根本原因,负荷构成是最直接的负荷本质特征,最能体现负荷特性分类的科学性和合理性[8-11]。而针对日负荷曲线进行聚类的研究者认为,电力负荷曲线聚类是配用电数据挖掘的基础,在负荷数据预处理、异常用户检测、需求侧管理与能效管理等多种配用电问题有广泛的应用[12-18]。
实际上,电力系统是一个高度复杂的分层系统,采用仅考虑日负荷曲线或是用户构成的聚类模型可以准确地对变电站进行聚类,但也相对地忽略了其他影响因素。例如,实际中存在变电站日负荷曲线相同而下属用户构成比例不同的情况,此时,如果只考虑日负荷曲线对变电站进行聚类,将会忽略变电站用户构成的差异。而在电网运行分析、电网规划中,往往既需要了解变电站的负荷变化特征,也需要了解变电站下附属用户的构成特征。
为此,本文提出同时考虑负荷曲线与用户构成的变电站聚类模型。该模型得到的聚类结果能反应变电站在日负荷曲线与用户构成上的区别,这种聚类结果可以视为对只考虑日负荷曲线的聚类结果的优化。由此提出一种聚类结果修正的算法,在对日负荷曲线数据采用K-means算法进行聚类并得到聚类结果后,采用该算法依据变电站用户构成数据修正K-means算法的聚类结果。该算法可以用于克服对高维数据聚类时经常发生的速度慢、精度差、易跌入局部最优的情况,同时可以更方便地确定最优聚类类数。
本文将介绍上述的新模型与新算法,考察其对变电站进行聚类的效果。算例验证首先采用人工构造算例分析两阶段聚类修正算法的合理性,之后采用实际数据验证聚类模型的实用性。
1 考虑负荷与构成的变电站聚类模型
电力系统可以看作一个分层的系统,设s个用户归属于同一个变电站i。忽略用户到变电站之间的复杂拓扑结构与通常相对较小的线路损耗,则变电站负荷可以看作是由底层用户构成的,如图1所示。

图1 用户到变电站的连接Fig.1 Connection diagram between users and substations
将变电站下属的用户依照其日负荷曲线不同,采用K-means算法和模糊C均值(FCM)聚类算法等分为n类,假设这n类用户的负荷总量在变电站中所占的比例分别为q1,q2,…,qn,则由上述n类用户组成的变电站用户构成的n维数据向量就可以表示为K=[q1,q2,…,qn]。
与此同时,假设变电站日负荷曲线数据为m维,记为P=[p1,p2,…,pm]。对于每一个待聚类的变电站,都有相应的数据向量K和P。据此,用于描述一个变电站特征的数据向量由两部分组成,即m维的日负荷曲线数据向量和n维的变电站的用户构成数据向量,为数据向量U=[K,P]。本文中主要研究日负荷曲线的形状,因此对数据进行了归一化。
聚类的最终目标是使所有类的类内距离之和最小,通常将目标函数S写为误差平方和的形式。即
(1)
式中:ci为数据点所属的聚类中心向量,表示第i类聚类中心;uj为归属于ci的第j个元素;h为归属于第i类的数据向量个数;D为数据点与聚类中心点之间的距离。
距离函数D选择欧氏距离为:
(2)
式中:ui为数据向量u的第i维;ci为数据点所属的聚类中心向量c的第i维。
求解该模型时需要注意的是,K和P数据向量的数据类型与数据维数有差异,将K和P合并为一个数据向量进行聚类是不合适的,因此采用先聚类,再修正的方法求解模型。而且现有的用户及变电站的量测数据以日负荷曲线数据为主,为获得变电站的用户构成类别,需要额外对用户进行一次聚类,用于判断用户的日负荷曲线类型并形成用于聚类的向量K。
2 两阶段聚类修正算法
2.1 两阶段聚类修正算法概述
本文求解上一节中模型的步骤为:首先,依照m维日负荷曲线数据向量P对变电站进行聚类,获得原始聚类结果;然后,依照n维用户构成数据向量K对原始聚类结果进行修正。在此将修正前的聚类结果称为仅考虑日负荷曲线的聚类结果,之后简称日负荷曲线聚类结果,其中包括第一次聚类后形成的聚类中心c0,以及各数据点归属于各个类的情况。
与聚类模型对应,该算法的目标是使所有类的类内距离之和最小,其目标函数式与距离函数式分别见式(1)和式(2)。
提出的两阶段聚类修正算法中考虑了以下问题:①加入用户构成数据后,类与类之间元素的转移;②类内差异较大时考虑类的分裂;③日负荷曲线数据与用户构成数据在聚类中所占权重的确定;④修正后最优类数的确定。
2.2 类与类之间的元素转移
加入用户构成数据K后,各数据点与各聚类中心的距离将会发生变化,聚类结果将随之发生变化,并偏离之前的最优结果。此时选择一部分离群数据,并判断这些离群数据是否应当从原来所属的类中移除并移入新的类中。
考虑到运算速度,本文选出距离所属聚类中心较远的一部分数据点作为离群数据。由此选择的具体方法为,设R为元素转移百分比,选择距离聚类中心最远、占数据点总数比例为R的一部分数据点作为待转移的数据点,被选出的距聚类中心较远的数据U在满足与其他的聚类中心的距离比与当前聚类中心的距离更近时,则移入距离最近的聚类中心。判断这些待转移的数据点是否真正转移的原则为,在现有的聚类中心中,若存在聚类中心c1与待转移的数据点距离更小。即
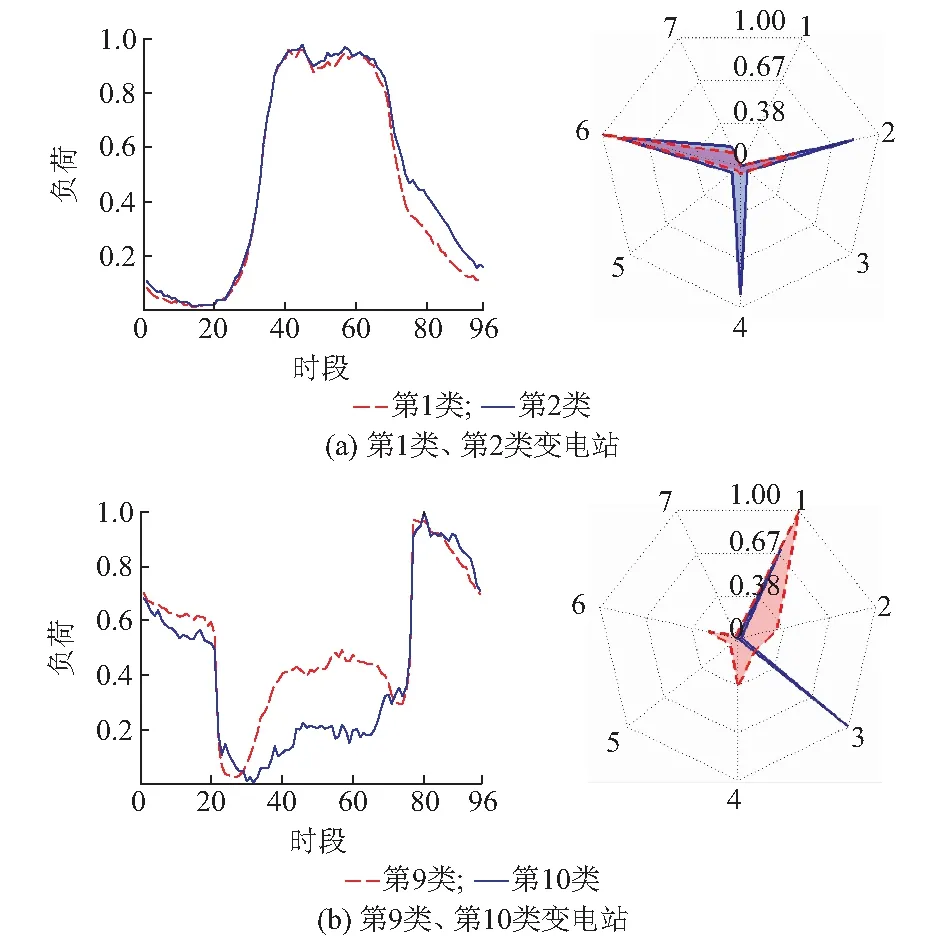
D(u,c1) (3) 则将该数据点从之前所属的聚类中心c0中去除,加入聚类中心c1。所有满足条件的元素都被转移后,取各类内数据的平均值为新的聚类中心。 设第i类聚类中心在元素转移后包含j个数据点,则新的聚类中心为: (4) 元素转移将会引起聚类中心的改变,应当重复上述步骤多次来得到一个稳定的结果。 在修正之前的数据已经被分成了数类,在修正后,最优类的数类可能会因为新特性的加入而增加,又因为每次类的分裂都会使目标函数S减小,所以选择使内部混乱的类分裂为小类。从初始类数k开始,类内距离最大的类将被分为两类。类内距离定义为: (5) 式中:Sl为第l类的类内距离;c′为ui所属的聚类中心。 如果存在Smax=max(S1,S2,…,Sk),则将Smax对应的类采用K-means算法分裂成两个类。在类的不断分裂过程中,类内距离之和将不断减小,直到达到预先设定的类数。 算法中采用分类适确性指标(DBI)判断分类类数是否达到最优,本文采用戴维森堡丁指数[19-20],也称为DBI,来确定最优聚类类数,其计算方法为: (6) DBI越小意味着类内距离越小,类间距离越大,分类效果越明显。由此,寻找DBI的最小值就可以快速确定最优类数。 日负荷曲线数据向量P和用户构成数据向量K的类型和数量级不同,因此在聚类过程中所占的权重也应当不同,所占权重较小的那部分数据的特征将更容易被忽略,相应的,这部分数据在聚类结果中的分布也会相对混乱。为使最终的目标函数S达到最小,选择合适的权重很必要[21]。 本文在确定权重时,首先基于两类数据的数值大小与数据维数差异按比例给出初始权重,之后在初始范围内考虑使目标函数最小的权重。考虑了权重的不同后,判断元素交换与聚类效果中所使用的距离函数Dq可由式(2)改写为: (7) 式中:a和b分别为原始数据与新增数据所占的权重;m和n分别为原始数据与新增数据的维数。 本文在后续算例中采用的权重计算方法为:首先设定计算步长为0.1,进行10次计算,找出目标函数值最小的点,之后在该点两侧区间内设定计算步长为0.01,以此逐步找出最优权重。 综上,本文所提聚类算法的详细步骤如下,算法流程图如附录A图A1所示。 步骤1:将用户日负荷曲线采用K-means算法进行聚类确定各用户的用户类型,采用DBI确定聚类类数。 步骤2:针对各个变电站的日负荷曲线数据采用K-means算法进行聚类,采用DBI确定聚类类数,获得变电站日负荷曲线聚类结果。 步骤3:在日负荷曲线聚类结果的基础上,考虑变电站中的用户构成比例,以之前的聚类结果为基础形成新的聚类中心向量。 步骤4:挑选各个类中距离类中心最远的、占比为R的部分数据向量,计算它们到其他聚类中心的距离,如果其中存在数据向量与其他的中心距离更近,则将这些数据点各自移入距离其最近的中心。 步骤5:取更新后的所有数据向量的平均值,生成新的聚类中心。 步骤6:迭代到类与类之间没有元素被交换、满足设定阈值或是设定迭代次数后停止迭代。 步骤7:将最大的类拆分为两个类,并重复步骤4至步骤6。如果类数达到设定的类数则停止,否则继续步骤4。最终获得算例结果。 本节通过一个构造算例,研究所提算法是否能使聚类结果准确体现各类变电站的用户构成特征。构造的算例以12 000条10 kV用户日负荷曲线为基础,人为设定100个变电站的用户构成比例,累加构成变电站日负荷曲线。 选择某地区来自浙江电网的12 000个经过修正与归一化的96个时段用户日负荷曲线数据,用户数据覆盖7大用电类型,包括大工业1 330个、居民生活1 423户、路灯30户、农业生产702户、非工业4 419户、商业3 024户、普通工业1 072户。本例中采用K-means算法,对底层用户日负荷曲线数据进行聚类,得到各用户的日负荷曲线类型。依照DBI确定最优类数为7类。获得的聚类如图2所示,图中负荷为标幺值。 图2中可见,各类用户负荷曲线之间差异明显,对应不同的用户群体。第一类用户用电负荷主要集中于晚间,对应如交通照明用电等错峰用电用户;第2,4,6,7类用户负荷为单峰型用电用户,以普通工业、普通商业、非工业负荷为主;第3类用户为晚高峰负荷,以居民用电负荷为主;5类用户则对应双峰用电型用电用户,农业用户、大工业用户占比较高。 图2 底层用户日负荷曲线聚类结果Fig.2 Clustering result of user profiles 获得12 000个用户各自所属的类别如表1所示,设定各个变电站中各类用户负荷占变电站总负荷的比例,将上节中得到的7类用户按比例分入100个变电站,将用户的日负荷曲线累加生成变电站日负荷曲线数据,即待聚类的向量P=[p1,p2,…,pm]。变电站依照设定的用户构成比例分为10种类型,表1中的每一行显示了该类变电站中各类用户的负荷所占的比例,由此获得待聚类的用户构成向量K=[q1,q2,…,qn]。 以1号变电站为例,这类变电站中,第2类用户负荷占变电站总负荷的40%,第6类用户负荷占变电站总负荷的60%。从12 000条用户日负荷曲线中选出总计100条第2类、第6类用户日负荷曲线,使它们各自的负荷之和分别占变电站总负荷40%与60%,之后将其累加作为变电站的日负荷曲线。 表1 变电站中各类用户所占比例Table 1 Proportion of users load for substations 表1中的1~6号、7~15号、16~20号及81~90号变电站由2~3种用户构成,用于研究算法对构成较为单纯的变电站的区分效果。其余的变电站则用于研究算法对构成较为复杂的变电站的聚类效果。 算例数据构成之后,按照第2节的聚类方法,首先采用K-means算法依据日负荷曲线数据向量P对变电站进行聚类,依照DBI确定聚类类数为3,获得初始聚类结果。将变电站分为3类,分别根据其特征将其称为日高峰用电类、双峰用电类与晚高峰用电类,分别对应表1中的1~50号、51~81号及8~100号变电站。附录A图A2显示了聚类中心及其周围的数据点的分布情况,日高峰类中包含的变电站数量最多,数据点也较为集中;晚高峰类变电站在白天部分略有分散,晚间的曲线形状基本一致。 为了体现用户构成方面的细节,采用之前介绍的两阶段聚类修正算法对前文所得的日负荷曲线聚类结果按照第2节中介绍的算法进行修正。兼顾计算速度与精度,元素转移百分比R取25%。在权重方面,日负荷曲线权重为0.6,构成数据权重为0.4时,计算目标函数值相对较小。由于算法中存在类的分裂过程,变电站类数由3类增加到10类,DBI在类数为10时达到最小值0.214 2,因此确定聚类类数为10类,结果中类数与表1中设定的10类吻合。 单峰类变电站因为构成数据的加入被分为了6类,6类中的负荷曲线非常相似,但在构成上有明显不同。图3(a)显示了其中的两类变电站,左侧为该类变电站的日负荷曲线,右侧显示变电站中的用户构成雷达图。与第1类相似,原始聚类结果中的双峰用电类(第2类)和晚高峰用电类(第3类)均被分为了两类。 图3(a)中显示了负荷曲线相似,但构成相差很大的两类变电站。这说明存在一些曲线类似而用户构成差异很大的变电站。图3(a)中的第1类所示变电站中第2类用户和第6类用户的负荷分别占总负荷的33.26%和57.63%,对应表1中的1~6号变电站。相应的第2类所示变电站中,第2,4,6类用户所占比例分别为28.16%,31.31%和30.49%,对应表1中设定的7~15号变电站。 图3 修正后的日高峰与晚高峰类变电站聚类结果Fig.3 Corrected results of daytime-peak and night-peak substations 图3(b)显示了构成复杂程度不同的两类变电站,分别对应构成较为单纯的81~90号变电站与构成较为复杂的91~100号变电站。这两组日负荷曲线相似的变电站也出现用户构成相差很大的情况。 类似地,除上文所示的4类变电站之外,其他6类变电站中普遍存在日负荷曲线形状类似,用户构成不同的情况。算法能有效修正日负荷曲线聚类结果,最终使聚类结果体现各变电站用户构成特征。同时算法也能有效区分构成单纯与构成复杂的变电站。 由目标函数S可知,采用欧氏距离作为变量之间的距离函数。每次迭代中朝一个变量ci的方向找到最优解,对每一个变量ci对式(1)中S指标求偏倒数之后使之等于0,可得聚类中心最优解为类内所有数据点数值的平均值。每次迭代都会使各类类内距离之和减小,因此该算法是稳定收敛的。但文中采用的目标函数—误差平方和是一个非凸函数,因此得到的解有可能是一个局部最优解。 为了验证算法克服局部最优的能力,本文中对比了该方法与常用的K-means算法的聚类效果,首先直接采用K-means算法对算例中的高维数据进行了1 000次聚类运算,之后将数据分为两部分,按照本文介绍的先聚类后修正的方法对同一组数据进行了1 000次聚类运算,初始聚类中心随机选取,并比较两者的效果。两者收敛时,修正算法所得的目标函数平均值、最值均小于K-means算法,详细对比如附录A表A1所示。 设单次目标函数值与该方法得到的最优值的差值不超过10%时,判断该结果近似为最优,则1 000次计算中,K-means算法达到近似最优163次,而本文提出的算法达到近似最优446次,说明该算法能显著降低聚类结果跌入局部最优的可能性。 K-means算法极易跌入局部最优,而采用两阶段聚类修正算法,将聚类过程拆分为一次聚类过程与多次修正过程后,即使在不优先确定聚类中心的情况下,算法收敛后的目标函数值也是相对稳定的。 采用浙江电网归属于39个220 kV变电站的12 000条用户日负荷曲线数据,根据其与下属用户之间的实际拓扑关系,通过用户归属于各个变电站的情况,得到变电站中7类用户的构成比例,形成待聚类的K,P数据向量。 对39座变电站的日负荷曲线数据进行聚类,将变电站日负荷曲线分为两类,即单峰型变电站与双峰型变电站。在此基础上采用本文介绍的两阶段聚类修正算法进行修正。在实际算例中,日负荷曲线权重为0.61,构成数据权重为0.39时,计算目标函数值相对较小。 在聚类类数增加过程中,采用DBI判断,指标在聚类类数为5类时达到最小值0.460 6。将最优聚类类数确定为5类。原聚类结果中类内聚类之和为255.88,修正后该值降低到了175.90。修正后得到的5类变电站的用户构成比例及归属于该类的变电站数量具体如附录A表A2所示,其中的7类用户的日负荷曲线与用户类型特征与图2中所示的一致。 如图4(a)所示,第2类和第5类变电站的日负荷曲线相似,均属于单峰型日负荷曲线,但是这两类变电站的用户构成相差较大;第2类变电站主要由第4类和第6类用户构成;第5类变电站成分相对平均;各类用户日负荷曲线见图3。这说明日负荷曲线相似的变电站用户构成比例可能不同。 除第4类变电站的用户构成与第1类变电站相似外,变电站之间构成区分明显,但如图4(b)所示,由于第1类变电站的日负荷曲线与第4类变电站的日负荷曲线有一定差别,所以这些用户构成非常相似的变电站被分为了两类,这表明构成相同的变电站可能存在日负荷曲线不同的状况。这种情况的出现是因为划分用户类别时,被划为同一类的用户的日负荷曲线可能存在差别,加之依照用户构成对变电站进行聚类时,同一类变电站的用户构成也会有所不同。误差被两次放大后,则会形成用户构成相同的变电站日负荷曲线不同的状况。 图4 修正后的变电站聚类结果Fig.4 Corrected clustering results of substations 第3类变电站在构成与日负荷曲线上与其他4类变电站均有较大差别。该类变电站日负荷曲线特征与用户构成特征见图4(c)。 本文提出同时考虑用户构成与日负荷曲线的聚类模型及两阶段聚类修正算法,将聚类过程拆分为一次聚类过程与多次修正过程。相比于直接采用K-means等传统算法对日负荷曲线与用户构成数据进行聚类,该方法提高了聚类准确性,满足了变电站特征精细分析的要求,简化了聚类类数确定过程,降低了聚类结果跌入局部最优概率,间接提高了负荷建模、负荷预测等研究工作的精度。本文对日负荷曲线的分析较为直接,直接将用户一天96个时段的负荷数据形成曲线并进行聚类,忽略了曲线中的一部分细节,在之后的研究中可以考虑将日负荷曲线分段进行分析,将聚类结果进行细化,从而体现用户与变电站的更多特征。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。2.3 类的分裂
2.4 最佳类数的确定
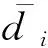
2.5 权重的确定
2.6 两阶段聚类修正算法流程
3 算例分析
3.1 底层用户日负荷曲线聚类

3.2 算例的构造

3.3 变电站日负荷曲线聚类结果
3.4 修正算法结果
3.5 算法的收敛性与合理性
4 实例分析

5 结语
