考虑爬坡功率有限平抑的高渗透率光伏电网储能配置策略
2018-08-09付爱慧
付爱慧, 张 峰, 张 利, 梁 军, 徐 震
(1. 电网智能化调度与控制教育部重点实验室(山东大学), 山东省济南市 250061;2. 山东大学能源与动力工程学院, 山东省济南市 250061)
0 引言
近年来,光伏发电技术在世界各地得到迅速发展,光伏发电渗透率也越来越高。与其他新能源发电相比,光伏发电的波动性和随机性更强,多云或雷阵雨天气发电功率在1 min内甚至会骤降60%以上[1-2]。在高渗透率光伏电网中,光伏发电功率的短期大幅度波动会引发系统频率波动,影响电网安全稳定运行[3-5]。储能系统(energy storage system,ESS)具有响应速度快、双向调节等优势,已成为应对光伏功率大幅度随机波动的重要途径[3]。但是,目前储能资源的价格比较昂贵,无法完全依赖ESS应对光伏发电的爬坡事件。因此,在高渗透率光伏电网中,对ESS进行优化配置,利用有限的储能容量实现光伏波动的有限平抑,将是保证高渗透率光伏电网频率稳定的重要方式。
目前,国内外学者对储能优化配置问题展开了较多研究,并取得了一定的理论成果。文献[6]分析了混合储能运行成本并根据循环寿命曲线建立电池寿命量化模型,最后以年均成本最小为目标确定储能容量;文献[7]考虑最佳期望输出与荷电状态(state of charge,SOC)适时调整的充放电策略,在此基础上以经济性为指标构建了储能容量优化模型;文献[8]通过分析光伏发电功率爬坡特性确定光伏波动平抑目标,结合系统发电能力和负荷需求等建立了以系统运行经济性最优为目标的储能优化模型;文献[9]从电网运行角度出发,采用饱和控制理论,以保证系统稳定为目标确定系统所需最小储能容量;文献[10]提出了一种基于风电功率预测误差分析的ESS规模确定方法,并建立了储能配置容量与风电场风能损失之间的成本与效益模型,进行储能容量规划。文献[11]将频谱分析和低通滤波相结合,得到并网联络线功率及储能充放电补偿功率,来确定满足平滑出力要求的最优储能额定功率、额定能量和初始SOC。上述研究对合理配置ESS容量、降低ESS运行成本、提高ESS运行经济性提供了很好的借鉴意义。但总体而言,已有的ESS容量配置方法中,尚未见有文献从光伏功率大幅度波动对电网调频备用需求影响的角度出发,来探究配置ESS降低高渗透率光伏电网调频备用的经济性和可行性;也鲜有文献从电网调频成本和ESS投资总成本的角度展开ESS容量优化配置的研究。
为此,本文以锂离子电池(lithium-ion battery,LiB)为ESS介质对高渗透率光伏电网进行储能配置。本文提出了一种考虑爬坡功率有限平抑的高渗透率光伏电网的储能配置策略,并基于SOC进行充放电功率动态调整。考虑到高渗透率光伏电网中,有功功率大幅度爬坡事件会增加电网的调频成本,本文建立了ESS投入后调频成本计算的数学模型,并以等效收益最大为优化目标实现ESS容量优化配置。最后,利用遗传算法对优化模型进行求解,并通过某高渗透率光伏电网负荷和光伏出力实际运行数据,验证本文所提ESS配置方法的合理性。本文的创新性在于:①提出了一种利用有限容量的ESS实现光伏爬坡功率有限平抑的控制策略,该策略兼顾了光伏发电入网需求和储能运行工况的合理性;②从光伏功率大幅度爬坡对电网调频备用需求影响的角度出发,考虑电网调频容量需求与ESS配置容量的相互制约关系建立储能容量优化模型,实现了储能容量的优化配置。
1 高渗透率光伏电网调频备用需求
1.1 等效负荷波动分析
高渗透率光伏电网中,电网需配置较大的调频备用容量调节光伏发电功率的大幅度爬坡。为分析光伏功率波动对系统频率调节备用需求量的影响,本文将其作为负的负荷与电网负荷进行叠加[12],得到光伏发电接入后的等效负荷。根据等效负荷的波动情况,确定系统所需调频备用容量。等效负荷的计算公式为:
Pd=Pload-Ppv
(1)
式中:Pd为电网等效负荷;Pload为电网实际负荷;Ppv为光伏发电功率。
附录A图A1反映了某高渗透率光伏电网叠加光伏出力后系统等效负荷波动情况,附录A图A1(a)和(b)分别为2016年1月和7月第一周光伏出力和负荷波动曲线。当光伏发电输出功率波动比较大时,叠加光伏出力将大大增加等效负荷的波动性。因此,为了接纳高比例的光伏发电,电网需要有足够的调节能力来维持系统频率稳定。
电网通过一次、二次和三次调频措施应对负荷变化引起的频率波动。其中,一次调频一般应对电网秒级的负荷波动;二次调频主要应对电网分钟级负荷波动;三次调频主要应对小时级负荷波动[13]。研究表明:光伏出力波动主要为分钟级波动,且最主要集中在5 min的时间尺度上[4]。所以,由光伏发电引起的频率波动将主要增加系统二次调频即自动发电控制(automatic generation control,AGC)的负担。
1.2 AGC容量需求分析
通过滚动平均法得到目标输出功率进而分离等效负荷的分钟级功率波动,得到分钟级等效负荷分量幅值和变化率。然后,根据概率分析得到系统所需AGC调节容量和调节速率。具体计算过程如下。
滚动平均法得到目标平抑输出:

Pd(t-(M-2))+…+Pd(t)+
Pd(t+1)+…+Pd(t+M))
(2)
式中:Pfd为经滚动平均后t时刻的负荷值;2M为滚动求平均的求解时域,M为求解向前或向后滚动时长。
分钟级负荷分量幅值:
Zd(t)=Pd(t)-Pfd(t)
(3)
分钟级负荷分量变化率:
Rd(t)=Zd(t+1)-Zd(t)
(4)
相关文献表明:负荷分量幅值和变化率分别服从标准差为σ1和σ2的正态分布,分别选取±3σ1和±3σ2为AGC调节容量和速率需求,即满足99.8%的调节需求,这样既能满足调节容量需求又能避免特殊运行工况甚至坏数据对计算结果的影响[14]。参照调频市场规则,本文以1 h为节点确定AGC调节容量和速率需求值,应对电网的分钟级负荷波动[15]。以附录A图A1中7月7日11:00为例计算AGC调节容量和功率需求,结果见附录A图A2。图中阴影部分为(-3σ,3σ),即(-11.75,11.75)MW和(-3.65,3.65)MW/min。从图中可以明显看出,绝大多数分钟级负荷分量和变化率均分布在此区间内。
ESS具有响应速度快、效率高等优点,能够更有效地平抑光伏出力的大幅度爬坡。电网配置一定容量ESS后,能够对光伏功率波动进行有效平抑,减小等效负荷波动,进而减小AGC的调节容量和功率需求[16]。在高渗透率光伏电网中配置ESS后,其等效负荷的计算公式为:
Pd′=Pload-(Ppv+Pess)
(5)
式中:Pd′为配置ESS后电网的等效负荷;Pess为ESS充放电功率,储能放电时为正值,即Pess>0,反之,充电时为负值,即Pess<0。
配置ESS后,电网的AGC容量需求将明显小于未配置ESS时的容量需求,而且随着ESS配置容量的加大,电网所需AGC容量会逐渐减小,AGC容量需求示意图见附录A图A3。同时,考虑到当前储能成本相对较高,其配置容量不可能无限增大。为此,本文将考虑ESS成本投入和节约的AGC成本之间的制约关系,对ESS进行优化配置。
2 储能控制策略
本文提出利用有限容量的ESS实现光伏爬坡功率有限平抑的控制策略。“有限平抑”的第一层含义为:只对光伏出力大幅度波动进行平滑。具体而言:在光伏出力出现大幅度爬坡时,通过储能的充放电对其进行平抑,减小电网调频备用容量需求;而在光伏发电功率波动比较小的时刻,为减小ESS的动作次数,提高其使用寿命,ESS不进行充放电。“有限平抑”的第二层含义为平抑结果是有限度的。具体而言:在平抑光伏出力大幅度波动时,平抑结果满足国家光伏入网标准即可,无需完全平抑成无波动状态。这种光伏爬坡功率有限平抑的方法能够在储能容量有限的情况下对光伏出力的大范围波动进行有效平抑。
本文选取LiB对光伏输出波动进行平抑。LiB是目前技术较为成熟的一种化学储能方式,相对于其他储能电池具有能量密度大、成本低和使用寿命长等诸多优点[14-18]。但LiB的充放电功率、充放电深度和SOC等都会影响它的功能和使用寿命,因此在使用过程中要避免出现过充过放现象。
2.1 ESS动作状态
电气行业对于爬坡事件的普遍定义为在单位时间内光伏发电输出功率的变化量超过某一限值。若时间区间Δt较短,可忽略Δt区间内爬坡事件的可能性,则光伏发电的爬坡率λ计算公式如下[19]:
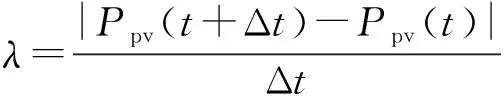
(6)
式中:Ppv(t+Δt)和Ppv(t)分为t+Δt和t时刻光伏发电输出功率。
本文定义爬坡事件为单位时间内爬坡率大于国家光伏入网标准,即λ>λval,其中λval为相关标准规定的光伏电站有功功率变化最大限值[20]。
基于光伏发电爬坡率的大小,将ESS分为3种动作状态。若光伏发电输出功率比较平缓,即未出现爬坡事件的情况下,ESS不动作;若当前时刻光伏输出功率变动剧烈,即出现大的爬坡事件的情况下,对光伏发电功率进行平抑。具体分类如下。
1)ESS不动作
若光伏发电输出功率比较平滑、未出现爬坡事件,则ESS不动作。具体表达式如下:

(7)
式中:Ppv(t)为当前时刻光伏发电功率;Pcom(t-Δt)为前一时刻经ESS平抑后的合成光伏输出功率,Pcom(t)=Pess(t)+Ppv(t);Δt为采样点间隔;Pess′(t)为储能充放电功率,其中Pess′(t)=0表示ESS不动作,Pess′(t)<0表示t时刻对ESS进行充电,Pess′(t)>0表示t时刻ESS放电。
2)ESS充电
在光伏发电输出功率突然增加、爬坡率比较大的情况下,ESS需要充电吸收多余电量,具体表达式如下:
Pess′(t)=(Pcom(t-Δt)+ΔP)-Ppv(t)
(8)
式中:ΔP为单位时间允许波动功率,一般来说ΔP=γλvalΔt(0<γ<1);Pess′(t)满足ESS配置的功率容量约束,即-PPESS≤Pess′(t)≤PPESS,其中PPESS为配置的ESS的额定充放电功率。
3)ESS放电
若光伏发电输出功率突然减小、爬坡率比较大的情况下,ESS需要立即放电弥补系统功率降低,具体表达式如下:
Pess′(t)=(Pcom(t-Δt)-ΔP)-Ppv(t)
(9)
式中:Pess′(t)满足ESS配置的功率容量约束,即-PPESS≤Pess′(t)≤PPESS。
2.2 基于SOC的充放电功率动态调整
SOC处于合理状态可提高LiB电池的使用寿命,本文根据ESS的实时SOC对ESS的充放电功率进行一定的调整。其中,Ssoc,max和Ssoc,min分别是LiB的SOC上限和下限警戒值,当Ssoc

表1 状态调整Table 1 States adjustment
表1中S2为ESS充放电功率为零状态;S1为正常充放电状态。S0为减放状态,合理减小ESS的放电功率;S5为减充状态,合理减小ESS的充电功率。以状态S0为例,对调整状态表进行详细解释。表中λ<-λval说明光伏出力出现大幅度骤降,满足2.1节式(9),需要通过ESS放电降低光伏功率的下行爬坡率。同时Ssoc
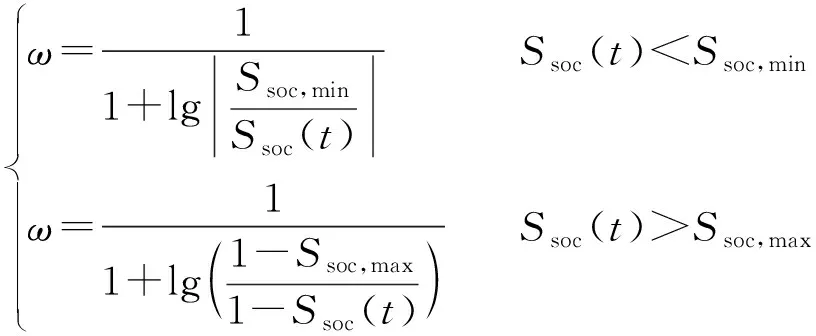
(10)
Pess(t)=ω(t)Pess′(t)
(11)
Pess(t)=Pcom(t-Δt)-Ppv(t)
(12)
Pess(t)=Pess′(t)
(13)
基于SOC的充放电功率动态调整过程为:首先,根据t时刻光伏出力爬坡率大小判断储能的运行方式,通过式(7)、式(8)、式(9)初步确定ESS充放电功率Pess′(t);然后,根据SOC进行充放电功率的动态调整,得到最终ESS充放电功率Pess(t);最后,为避免过充过放,进行充放电功率约束:-PPESS≤Pess(t)≤PPESS。具体流程图见附录A图A4。
3 储能配置优化模型
3.1 目标函数
ESS的投入可以降低高渗透率光伏电网调频备用的需求容量,而同时配置ESS需要相应的投资成本。因此高渗透率光伏电网中,电网调频备用容量与ESS配置容量存在相互制约关系。本文以电网调频成本和ESS投资成本之和作为等效成本,并以投入ESS前后等效成本的差值作为等效收益J。储能配置优化模型以等效收益J最大为目标函数,对ESS的能量容量和功率容量配置进行优化。其中,配置ESS前的总成本为AGC调频成本FAGC;配置ESS后的成本为ESS成本Fess和AGC调频成本FAGC′的总和。目标函数为:
maxJ=FAGC-(FAGC′+Fess)
(14)
为方便计算,本文中配置ESS后,AGC年度调频成本对应计算参数以上标“′”进行区别。
3.1.1ESS的年度成本计算
由于光伏发电功率具有明显的年度周期性,本文以一年为计算周期对ESS容量进行优化配置。相应的,ESS的成本计算需要等效为年度成本。具体而言,ESS的成本由建设成本和维护成本组成,其中投资建设成本主要包括能量转换装置(power control system,PCS)总成本及储能单元(energy storage unit,ESU)总成本两部分,年度成本根据使用寿命进行统一评估,具体公式如下:
Fess=Cb,esu+Cb,pcs+Ce
(15)
式中:Cb,esu为ESU的建设成本年度分摊值;Cb,pcs为PCS的建设成本年度分摊值;Ce为年度维护成本。
1)在ESS的寿命周期内,ESU成本主要与ESS的能量容量相关,而PCS成本与ESS的功率容量直接相关。由此,分别得到ESU和PCS年度建设成本如式(16)和式(17)所示[21]。
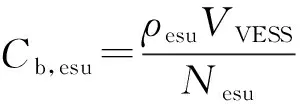
(16)

(17)
式中:ρesu为ESU单位能量容量建设成本;ρpcs为PCS单位功率容量建设成本;VVESS为ESS配置能量容量;PPESS为ESS配置功率容量;Npcs为PCS运行年限,使用年限一般取项目周期20年[22];Nesu为ESU等效运行年限,与电池的使用方式和性能有关。
ESU的使用寿命受工作方式影响明显,尤其是放电深度(depth of discharge,DOD)对其寿命影响较大。Nesu的计算过程为:首先,计算ESS的充放电循环次数和每次充放电的放电深度差(ΔD);然后,根据循环寿命与ΔD的关系得到每个放电周期的等效寿命损耗;最后,计算电池年寿命损耗,得到电池等效使用年限[23]。
循环次数和ΔD的计算参考文献[24]进行半周期统计,图1为ESS充放电半周期充放电循环次数和ΔD计算示意图。每次计算从ESS充放电转换的时刻进行,即在SOC曲线峰谷值处进行统计。如图1所示,折线A-B-C-D-E-F代表电池SOC变化曲线,B,C,D,E点为SOC曲线的峰谷值,即半周期计算的起始点。故图中可得计数半周期1(A-B,ΔD=0.36)、半周期2(B-C,ΔD=0.11)、半周期3(C-D,ΔD=0.19)、半周期4(D-E,ΔD=0.30)和半周期5(E-F,ΔD=0.28)。

图1 半周期统计示意图Fig.1 Schematic diagram of semi-periodic statistics method
ESS循环寿命与ΔD关系拟合曲线采用幂函数表示[25]:

(18)
式中:Di为第i次充放电半周期的放电深度差;Lcd1为放电深度差是100%时的循环寿命;Lcd(Di)为放电深度差是Di时的循环寿命;kp为对储能厂家提供的电池“循环寿命—放电深度实验数据”进行拟合得到的常数。假设Lcd1=5 000,不同kp值下,ESS循环寿命随不同放电深度差的变化曲线见附录A图A5。
第i次充放电对ESS的寿命损耗百分比为循环次数的倒数,具体计算公式为:

(19)
式中:H为第i次充放电半周期中当放电深度差为Di时对应ESS的寿命损耗。
ESU的等效使用年限为:

(20)
式中:Hd,i为第d天i次充放电半周期对电池寿命的损耗;k为统计得到的日充放电半周期数;Dy为一年中ESU的工作天数。
2)ESS的年运行维护成本包括人力、管理费用等固定成本,以及电费、燃料费等可变维护成本。运行维护费用Ce=μ(Cb,esu+Cb,pcs),μ为ESS运行维护成本与初始投资的比值,一般取值为2%[21]。
由此,ESS成本费用年值计算公式如下:
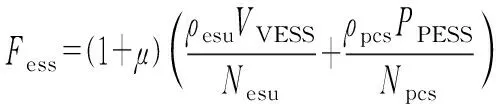
(21)
3.1.2AGC年度调频成本计算
按照2011年美国联邦能源监管委员会(FERC)的755号命令[26],电力市场调频服务费用结算方式相继推出两部制结算规则,即兼顾调频容量和里程的结算方式,具体的计算过程如下:
Fv=pVVAGC
(22)
Fm=pMMAGCScore
(23)
式中:pV和pM分别为AGC购买调频容量单价和调频里程单价;VAGC为机组的总中标容量;MAGC为机组在该调频时段的实际调频里程,其测算方法参照美国CASIO电力市场最新规则[27];Score为调频效果得分,Score针对每台机组提供AGC服务进行量化评价。Score一般由准确度、延时和精确度三者加权相加得到,取值在0~1之间。因每个机组调频补偿价格不是本文研究重点,为方便计算,Score均取值为1。
实际调频里程MAGC的计算过程如下:①当AGC机组向上调节时,若j+1时刻机组响应值小于指令值,按照机组响应的实际调频里程进行付费;若j+1时刻机组响应值大于指令值,按照指令调频里程进行付费,超调部分不进行付费,具体公式为如式(24)所示。②AGC机组向下调节时,若j+1时刻机组响应值小于指令值时,按照机组指令调频里程进行付费,超调部分不进行付费;若j+1时刻机组响应值大于指令值时,按照机组响应的实际调频里程进行付费,具体公式如式(25)所示。
(24)
(25)
式中:SRE,j为与时刻j的指令值对应的机组响应值;SRE,j+1为下一时刻的机组响应值;SAGC,j和SAGC,j+1分别为在j和j+1时刻的AGC指令。
计算调频时段内每一采样点间隔内的实际调频里程进行累加,便得到该调频时段实际调频里程之和。由此,配置ESS前系统总的调频成本计算公式如下:

(26)
式中:VAGC,d,i为第d天第i个时段AGC的配置容量;MAGC,d,i为第d天第i个时段AGC的调频里程;为方便计算,本文AGC调节容量单价pV和调频里程单价pM根据调频市场历史价格设为定值。
高渗透率光伏系统配置ESS前后,AGC年度调频成本计算方式完全相同,只是配置ESS后,光伏输出大幅度爬坡会得到有效平抑,AGC的配置容量和调频里程会减小,年度调频成本也会随之降低。根据各参数的求解模型,本文ESS容量优化模型的目标函数如式(27)所示。
maxJ=
(27)
式中:第一部分为未配置ESS时,电网AGC的年度总调频成本;第二部分为ESS的等效年度成本和配置ESS后电网的AGC年度总调频成本之和;两者做差即为配置ESS后,电网的等效收益J。
3.2 约束条件
ESS配置功率容量需要满足相应储能介质的功率约束:
-Pd,max≤PPESS≤Pc,max
(28)
式中:Pc,max和Pd,max分别为相应介质对应的目前最大充放电功率。
AGC的调节速率响应值需满足电网AGC最大调节速率约束:
-Sd,max≤SRE≤Su,max
(29)
式中:Sd,max和Su,max分别为高渗透率光伏电网中所有提供AGC调频机组的向下和向上最大调节速率能力。
3.3 求解算法
利用全局搜索能力强、计算效率高的遗传算法(GA)对优化模型就行求解计算,具体的算法及计算步骤如下。
步骤1:创建一个随机种群,最优解将通过初始假设进化求得。
步骤2:计算光伏输出爬坡率,若出现爬坡事件,采取状态S2,S3,S4对应的充放电策略;若未出现爬坡事件,采取状态S0,S1,S5对应的充放电策略。
步骤3:按照式(15)—式(26)计算各成本参数,式(27)计算适应度值。
步骤4:当最优个体的适应度和群体适应度不再上升则算法的迭代过程收敛,算法结束,否则根据它们的适应值和式(28)和式(29)约束条件选择父辈,通过繁殖、交叉、变异形成下一代,并重复步骤2和步骤3。
4 验证分析
以某高渗透率光伏电网的实际运行数据来验证本文方法的有效性。该小型电网以火力发电和光伏发电为主,火电机组装机容量为360 MW,光伏发电装机总容量为72 MW,光伏渗透率为16.7%,具体装机情况见附录A表A1。电网的典型日负荷曲线如附录A图A1所示,其高峰负荷接近340 MW,低谷负荷为180 MW左右。
提取该电网2016年一年的光伏电站运行数据和负荷数据验证本文所提方法的有效性,依据最新相关数据[14-18,20,22-23,26-27],本文相关计算参数值见附录A表A2。本文所提储能容量优化策略计算结果:FAGC=4 349 854美元,FAGC′=5 209 672美元,VVESS,best=6.271 2 MW·h,Fess=363 796美元,J=496 022美元,PPESS,best=7.234 2 MW。
由本文方法计算得到高渗透率光伏电网ESS最优配置能量容量为6.271 2 MW·h,最优配置功率容量为7.234 2 MW。ESS的年度成本费用为363 796美元,节约的AGC调频费用为859 818美元,故配置ESS的等效收益为496 022美元。
从计算结果可以看出,通过配置ESS后系统存在较高的等效收益,大幅度提高了系统的运行经济性。附录A图A6为此电网随ESS配置能量容量和功率容量变化的等效收益等高线图。
ESS配置的能量容量和功率容量均会影响电网的等效收益,当能量容量一定时,随着ESS功率容量增大时,等效收益先增大后减小;当ESS功率容量一定时,随着配置能量容量的增加,等效收益先增大,随后减小。由此可得:①在ESS优化过程中,存在最优的配置能量容量和功率容量,使得等效收益最大;②当ESS配置过大时,造成资源的浪费,等效收益越来越小甚至为零。为进一步验证所提优化方法的有效性,本文接下来分别从高渗透率光伏系统配置ESS的经济性和ESS平抑效果两方面进行分析。
4.1 配置ESS的经济性验证
为考察不同ESS能量容量配置情况下系统运行成本和等效收益变化情况,在最优配置功率容量的前提下,选取不同的ESS配置能量容量进行分析。随着ESS配置能量容量的不同,等效收益和ESS成本变化趋势如图2所示。

图2 成本曲线Fig.2 Cost curves
由图2可见,随着ESS配置能量容量增加,AGC节约的成本ΔFAGC越来越多,但增加单位VVESS对AGC调频成本的降低作用越来越微弱;随着ESS配置能量容量增加,其年度建设运行成本几乎呈线性增加趋势。所以,需合理确定VVESS才能使系统等效收益最高。等效收益方面,VVESS<6.3 MW·h时,随着ESS的配置能量容量增加,等效收益逐渐提高;VVESS>6.3 MW·h时,等效收益逐渐降低,在储能能量容量超过34.5 MW·h时等效收益甚至为负值,即配置ESS后系统调频总成本反而会提高。综上所述,当ESS配置能量容量适度时,储能能量容量的增加会明显减小电网调频成本,提高系统运行经济性;但当ESS配置能量容量较大时,配置能量容量的增加难以带来明显的经济效益,反而会出现负收益。
为了进一步深入研究配置ESS的等效收益情况,本文以一天为周期对配置ESS后电网的等效收益进行分析。配置ESS后,2016年日等效收益统计图如附录A图A7所示。配置ESS(容量为6.271 2 MW·h/7.234 2 MW)后,收益为正的天数比例为63.59%,收益为负的天数占36.41%。收益为负时日损失金额一般不超过-1 200美元;而相对于损失,收益均值较高,其峰值甚至接近11 600美元,故配置ESS仍有可观的年等效收益。
4.2 配置ESS的平抑效果验证
算例1:ESS的配置容量在较大程度上会影响电网负荷功率的平抑效果。本文定义日平均功率波动强度β来衡量功率波动大小,其定义为:

(30)
式中:Pd′(t)为电网等效负荷;tst和ted分别为所选负荷和光伏输出功率数据时间区间的初始时刻和结束时刻。以2016年全年运行数据进行分析,以最优配置能量容量VVESS,best为基准值,分别选取ESS能量容量标幺值0.1,0.5,1,1.5,2.0,计算日平均功率波动强度,结果如表2所示。

表2 计算结果Table 2 Calculation results
由表2中计算结果可以看出,随着ESS配置能量容量的增加,β逐渐减小,即高渗透率光伏电网的等效负荷波动逐渐减小。当配置最优储能能量容量时,与仅配置10%最优能量容量相比,β降低了37.7%,对系统稳定运行起到较为积极的作用。值得注意的是,当ESS配置能量容量超过最优配置能量容量后,增加ESS能量容量配置对等效负荷功率的波动强度改善效果相对较小,说明等效负荷已经达到相对较平滑的状态。
算例2:本文为减小ESS过充过放现象,本文ESS控制策略中进行了基于SOC的ESS充放电功率动态调整。为充分说明进行SOC动态调整的作用,选取某天光伏平抑过程进行对比,如附录A图A8所示。由该图可见,通过SOC进行动态调整,能够有效减小ESS过充过放次数,使LiB的SOC处于合理的运行区间,提高电池使用寿命,增加日等效收益。
算例3:由于光伏发电功率受天气因素影响非常明显。选取典型天气进行ESS平抑效果验证分析。晴、多云、阴天和雨天4种典型天气下,日等效收益分别为-1 106美元、8 532美元、1 732美元和-989美元。图3为对应日光伏发电出力波动的平抑效果图,图4为对应ESS的SOC变化状况。

图3 典型天气平抑效果曲线Fig.3 Smoothing effect curves in the typical weather
图3(a)所示晴天光伏出力一天未出现大幅度波动,ESS充放电功率为零,对应图4(a)中SOC值不变。即使ESS没有进行充放电,仍有分摊的ESS配置和运行成本,故等效收益为负数(-1 106美元)。图3(b)所示多云天11:00—16:00光伏发电功率出现频繁波动。在此期间通过ESS的充放电对光伏大幅度爬坡事件进行有效平抑,期间ESS的SOC都在合理范围内变化。通过配置ESS,光伏出力的大爬坡事件得到有效改善,在典型日中对应当天日等效收益(8 532美元)最高。图3(c)所示阴天光伏出力爬坡事件出现次数与多云天相比有所减少,但持续时间增长。所以ESS充放电次数比多云天少,但ESS单次充放电能量变大,故SOC的变化幅度比较大。图3(d)所示雨天光伏发电功率小,波动幅值也小,故ESS基本不动作。配置ESS的收益不抵其运行和配置费用,故等效收益为负。
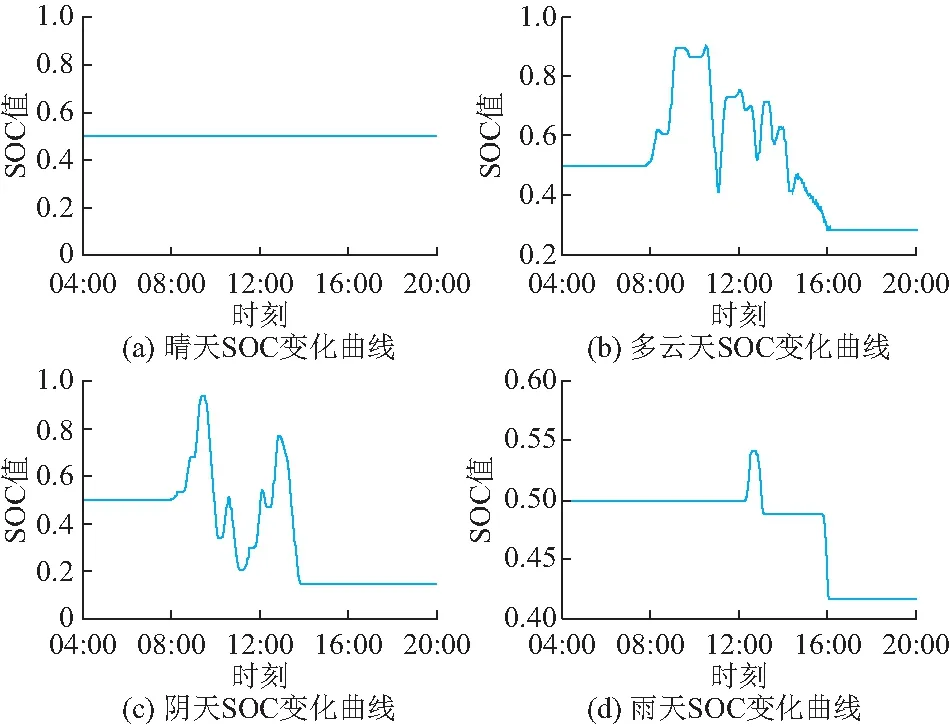
图4 典型天气对应SOC曲线Fig.4 SOC curves in the typical weather
由上述分析可知:不同天气情况下,ESS发挥的作用和日等效收益会有明显的不同。多云和阴天情况下,高渗透率光伏系统配置ESS的等效收益最大;晴天和阴雨天配置ESS甚至会有一定损失,更进一步验证了附录A图A7日等效收益变化的结果。在天气多变的高渗透率光伏发电地区,配置ESS更具有必要性。
综上所述,本文所提的储能容量优化方法不仅能够增加等效收益,提高系统运行经济性,而且在储能充放电策略引导下,可有效处理光伏输出功率的大幅度爬坡事件,减少光伏大幅度波动对电网频率的不利影响,提高系统运行稳定性。
5 结语
本文为兼顾光伏发电入网要求和电网运行经济性,提出了一种光伏波动有限平抑的ESS充放电控制策略,在平抑光伏出力大幅度波动的前提下,减小ESS的充放电次数,提高其使用寿命。并且,针对高渗透率光伏电网储能的容量优化问题,本文重点考虑电网调频容量需求与ESS配置容量的相互制约关系,从最优化高渗透率光伏电网调频费用出发,提出了建立以配置ESS后等效收益最大为目标的储能容量优化模型。本文所提储能配置策略能够对光伏发电功率大幅度爬坡进行有效平抑,而且使电网等效收益最高,从而在控制电网频率稳定和经济效益之间取得一定的平衡。此外,本文的研究成果对提高电网新能源发电渗透率的研究具有一定的参考意义。但是,本文储能的配置方式为集中式配置,鉴于未来电网结构的复杂性,还需进一步考虑储能分布式配置的配置效果和经济性。
本文得到山东大学青年学者未来计划和山东大学基本科研业务费资金(2017JC039)的资助,谨此致谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
