基于定常海森矩阵的配电网三相最优潮流模型

2018-08-09赵婷婷赵凤展巨云涛杜松怀周献飞

电力系统自动化 2018年15期

赵婷婷, 赵凤展, 巨云涛, 杜松怀, 张宇, 周献飞

(1. 中国农业大学信息与电气工程学院, 北京市100083; 2. 国网北京市电力公司, 北京市 100031)

0 引言

含有高比例分布式电源(distributed generator,DG)和多种离散可调设备的主动配电网最优潮流问题需综合考虑高比例DG对配电网潮流分布的影响,通过优化电网中可调设备的运行策略,实现运行成本最低或网损最小的目的,其实质上是一个离散变量和连续变量共存的非凸、非线性规划问题。实际电网中含有的离散可调设备包括补偿电容器、有载调压变压器等,其在电力系统最优潮流、改善系统节点电压、减小网络损耗等方面起到重要作用。

随着分布式光伏电源等DG的接入,配电网的节点电压越限问题越来越严重。高比例DG的接入对电网的稳态潮流分布及节点电压产生重大影响[1-7],解决节点电压越限问题需要高效率的最优潮流算法。文献[6]研究了风速的不确定性、不同风电场之间风速的相关性对最优潮流的影响。文献[7]建立了含有载调压变压器的主动配电网最优潮流模型,提出了一种基于分段线性化的有载调压变压器的准确建模方法,并应用二阶锥松弛法求解所建立的最优潮流模型。文献[8]考虑DG非耦合模型下的主动配电网优化运行,其得到的结果是近似结果而不是准确的结果。文献[9]建立了DG三相稳态模型,其详细模型可应用于主动配电网最优潮流计算。

原对偶内点法因具有计算速度快、收敛性好等优点被普遍应用于解决传统电力网络最优潮流问题[10-20]。文献[13]提出一种基于高斯罚函数的离散变量处理方法,但其并没有深入对比说明该方法较其他罚函数(如文献[20]中的二次罚函数)在计算效率方面的优势。文献[14]在有载调压变压器模型中引入虚拟节点,将优化问题变为直角坐标系下的二次模型,缩短了无功优化问题的求解时间。

本文结合目前配电网最优潮流研究现状,建立三相变压器的二次模型,使最优潮流模型的海森矩阵为常数阵,从而降低求解时间。建立了分布式光伏电源三相功率耦合的不对称注入模型,提高DG接入主动配电网分析的精确性。应用内嵌罚函数的内点法求解含离散控制变量的配电网三相最优潮流,同时,加入调压器对系统节点电压进行分相微调,进一步优化目标函数值。最后,通过算例验证本文所提模型及算法的正确性与有效性。

1 三相配电网模型

1.1 三相变压器模型

直角坐标系下的最优潮流模型,变压器变比通常表示为两端节点电压幅值的比,导致最优潮流模型是高于二次的非线性优化问题,应用内点法进行计算时,海森矩阵会随着迭代而更新,影响了求解速率[14,21]。为了克服这个问题,本文建立了新的三相变压器二次模型,使最优潮流计算过程中海森矩阵变成常数。下面以星形—三角形变压器对该模型进行说明,但模型的适用性不只限于星形—三角形变压器。

附录A图A1所示为星形—三角形变压器支路ij,在中间加入虚拟节点m,使变压器支路变成由理想变压器(变比为k)支路im与变压器阻抗(阻抗为R+jX)支路mj这两条支路的组合。图中标有各节点的电压向量和支路电流向量。

根据理想变比线圈定义,有

(1)

根据能量守恒定理,有

(2)

可以得到:

(3)

三相系统中,在标幺值转换时,电压参考值是节点电压,线电压的基值为节点电压,对于星形—三角形变压器,标准变比为1∶1.732。

变压器阻抗支路mj可作为一条普通阻抗支路进行处理,有式(4)成立:

(4)

在如上变压器模型中,以各节点(如附录A图A1中的节点i,m,j)三相电压和三相支路电流为状态变量(相对于传统模型,增加了三相支路电流为状态变量),变压器变比k为控制变量,约束条件为各支路三相的KCL和KVL方程,由此形成了不高于二阶的三相变压器二次模型,其二阶导数为常数,从而构成了最优潮流模型的定常海森矩阵的一部分。

1.2 分布式光伏电源三相模型

三相的DG通常建立序分量电路建模。不同类型的DG包括以电压型逆变器为接口的DG、双馈异步风力发电机、同步发电机等。本文以广泛应用的光伏DG为研究对象,提出其三相二次模型。无特殊说明,下文所提DG均指光伏DG。

图1 DG序分量模型Fig.1 Sequence component model of DG

DG的序分量模型被连接到三相电路,通过相序转化成各相分量。本文通过改进文献[22]中DG的相—序耦合模型,提出DG相—序耦合的二次模型,选取DG总的注入电流和端口电压的相分量为未知量,根据相序转换公式,可以得到DG各序的节点电压和支路电流,即Ip,re+jIp,im,In,re+jIn,im,I0,re+jI0,im,Up,re+jUp,im,Un,re+jUn,im,U0,re+jU0,im。

DG的序分量约束如下:

(5)

(6)

(7)

式(5)—式(7)所示DG等式约束考虑了三相功率耦合的特点,这与文献[22]的稳态模型不同,文献[22]的序分量控制没有考虑不对称情况。该DG方程是线性二次方程式,因此可以保证含DG的最优潮流计算过程中的海森矩阵是恒定的。

而在三相配电网最优潮流中,常见使用DG的三相非耦合模型[8]如下:

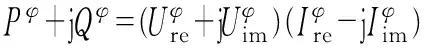
(8)

式中:P和Q分别表示DG输出的有功功率和无功功率;U和I分别表示DG节点电压和注入电流;上标φ表示A,B,C相中的一相。

因此,本文考虑三相功率耦合特性的DG模型是精确的模型,而如式(8)所示的DG三相非耦合模型是近似的模型,在最优潮流计算中,其得到的结果没有三相耦合模型的结果精确。

1.3 三相调压器模型

调压器串联接入电网,用于配电网电压的分相微调。三相星形调压器由三个单相调压器星形连接构成,3个调压器各自改变分接头位置,其接线方式见附录A图A2。

该模型满足以下等式约束关系:

(9)

(10)

(11)

式中:负号用于降压,正号用于升压;Ttap表示调压器分接头的位置(通常有32级调节,其调节范围为-10%～10%),是由线路压降补偿器依据负荷中心的电压来控制的,补偿器通过电压互感器(变比NPT∶1)和电流互感器(变比CP∶CS)连接在配电线路上,接线图见附录A图A3。补偿器阻抗的设定值表示从调压器到负荷中心的等效阻抗,公式如式(12)所示。

(12)

负荷中心的电压为(以a相为例)为:

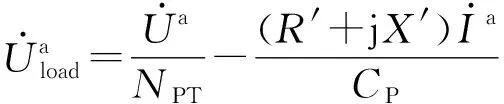
(13)

如果负荷中心的电压水平为120 V,带宽为2 V,则调压器分接头挡位每变化一挡,电压将变化0.75 V,升压、降压时分接头改变的次数近似为(以a相为例):

(14)

2 三相最优潮流模型及算法

2.1 定常海森矩阵最优潮流模型

以各节点的三相电压和支路三相电流为状态变量,建立三相配电网的最优潮流模型,其简化模型如下:

(15)

其中,目标函数为网络总损耗最小,如式(16)所示。

(16)

等式约束条件包括以下几项。

1)变压器支路约束,见式(1)、式(3)和式(4)。

2)DG支路约束,见式(5)—式(7)。

3)调压器支路约束,见式(9)和式(10)。

4)各阻抗支路三相的KVL和KCL方程：

(17)

式中:Ur,re和Ur,im分别为支路电压实部和虚部矩阵；Ui,re和Ui,im分别为节点电压实部和虚部矩阵；Ir,re和Ir,im分别为支路电流实部和虚部矩阵；A为节点支路关联矩阵,AT为其转置。对于三相四线制配电网,将中性线处理成接地支路;对于缺相运行的配电网,只列出已有相的支路方程即可。

不等式约束条件包括如下状态变量约束和控制变量约束。

1)状态变量约束,含各发电机有功及无功出力约束、节点电压幅值约束,如式(18)所示。

(18)

式中：SG和SB分别为发电机和电网节点集合。

2)控制变量约束,包括变压器分接头挡位KT、调压器分接头挡位KV、无功补偿电容器投切容量QC,如式(19)所示。

(19)

式中：ST,SV,SC分别为变压器、调压器和无功补偿电容器集合。

由此可见,该模型中各公式的最高阶数不超过二阶。因此,应用内点法对该模型进行求解时,其海森矩阵为常数阵。本文应用具有收敛速度快、稳定性能好等优点的预估—校正原对偶内点法[10]对优化模型进行求解。

2.2 离散变量连续化处理

主动配电网最优潮流问题中具有离散控制变量(如变压器分接头位置、无功补偿电容器容量等),在原目标函数中引入罚函数可将离散变量进行归整,即使得原目标函数中附加了一项由离散变量引起的虚拟损耗,可将连续值就近靠拢取得离散值。目前比较有效的有二次罚函数[20]和高斯罚函数[13],二者的表达式分别如式(20)和式(21)所示。

(20)

(21)

式中:N为离散变量数量;v为惩罚因子;x=(xi)为离散控制变量;b=(bi)为各离散控制变量的一组离散值；c=(ci)为邻域大小因子，为常数。惩罚函数值随着向量x=[x1,x2,…,xN]T中xi与bi的距离的减小而下降为零。

将罚函数扩展到目标函数式(16)中,得:

(22)

当惩罚因子足够大的时候,为使目标函数达到最小值,离散控制变量将被优化到相应的离散值,从而使惩罚函数值变为零。

高斯罚函数与二次罚函数相比,有更快的下降速度,对离散变量的变化更敏感;但二次罚函数是二阶函数,其二阶导数为常数,而高斯罚函数为高阶函数,其二阶导数会随着自变量的变化而改变。二者计算效果和速度的比较将在后面的算例分析中给出。

2.3 最优潮流二级迭代优化策略

为了实现系统节点电压优化和最小化网损的目的,利用发电机、变压器、无功补偿电容器和DG的可控性及调压器分相微调电压的功能,本文设计了基于二级迭代的最优潮流控制策略。其中,一级迭代优化是指固定调压器分接头变比,通过调节发电机无功出力、变压器分接头、投切无功补偿电容器、控制DG出力,对系统进行最优潮流计算,使系统的有功损耗达到最小;二级迭代优化是指根据一级迭代优化结果更新调压器分接头变比,对系统电压进行分相微调。

具体步骤如下。

步骤1:设调压器的分接头位置为1。

步骤2:进行最优潮流计算(此时,调压器的分接头位置不参与优化),得出发电机无功出力、可调变压器分接头位置、分布式电容器投切位置及容量、DG的有功、无功出力。

步骤3:根据步骤2的最优潮流计算结果,并根据负荷中心节点电压理想值范围目标,由式(11)至式(14)计算调压器变比。

之后,根据新的调压器分接头位置,再返回步骤2重新计算最优潮流,后步骤3计算调压器分接头新的位置。如此反复计算,直到负荷中心的电压在期望的理想值范围内,迭代结束。

3 算例分析

应用MATLAB符号运算工具箱对本文所提的基于定常海森矩阵的配电网三相最优潮流模型进行仿真分析。针对图2所示的修正配电网IEEE 13节点测试系统进行分析。

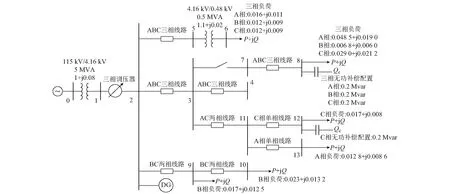
图2 IEEE 13节点修正系统接线图Fig.2 Wiring diagram of modified IEEE 13-bus system

图2中标出了变压器的参数(变比、额定容量、阻抗参数)、线路的相数(省略了线路的阻抗和导纳参数)、负荷参数、无功补偿配置容量等。算例中的控制变量为发电机无功出力、DG出力、变压器变比的调整和无功补偿电容器(节点8和节点12的分相电容器)的投切,其中变压器变比和电容器是离散控制变量。设变压器变比范围为0.90～1.10,共分为8挡,分级步长为0.025。电容器的最大无功出力为0.02(标幺值),分级步长为0.01(标幺值)。所有节点的电压范围为0.9～1.1(标幺值)。调压器分接头有32级调节,调节范围为-10%～10%,负荷中心设在节点3,其电压水平为120 V,带宽为2 V。

3.1 三相配电变压器二次模型的验证分析

针对修正IEEE 13节点三相配电系统,为了验证本文提出的用于主动配电网最优潮流问题的三相变压器模型的合理性,针对三相配电网的传统三相变压器非二次模型[21]与本文提出的三相变压器二次模型,应用基于二次罚函数的预估—校正原对偶内点法进行最优潮流计算,结果如表1所示。

表1 不同变压器模型优化结果Table 1 Optimization results of different transformer models

由表1可知,应用两种模型的网络损耗相同,但是本文所提三相变压器二次模型较非二次模型大大提高了计算速度。其原因是,在最优潮流计算过程中,本文提出的三相变压器的二次模型及其他设备的不高于二次模型的海森矩阵为常数,在迭代过程中只需要计算一次,每次迭代不需要重新计算,从而大大减少了计算时间;而传统的三相变压器的非二次模型的海森矩阵不为常数,每次迭代都要重新计算,如表1所示,算例需要计算17次,这使得计算时间显著增加。

另外,两种模型的计算时间都比较长,这是因为优化过程中的海森矩阵是基于MATLAB符号运算自动微分生成的,计算海森矩阵的速度较慢,但这对算例得到的结论没有影响。算例中优化迭代次数是17次,在计算机上,单纯计算一次海森矩阵需要6.696 465 s,所以非定常海森矩阵模型中海森矩阵的计算时间保守估计是一次计算的17倍,即113.84 s。由此,表1中的计算时间是合理的。

3.2 最优潮流算法及其离散变量连续化处理算法的比较分析

为了比较二次罚函数与高斯罚函数的收敛特性及对优化算法的计算时间的影响,设计了嵌入二次罚函数的预估—校正原对偶内点法(方法A)和嵌入高斯罚函数的预估—校正原对偶内点法(方法B)的最优潮流对比试验。分别用这两种算法对修正IEEE 13节点三相配电系统进行最优潮流计算,通过比较各算法的优化结果(网络损耗)、迭代次数、收敛精度为e-10、计算时间等,证明各方法的优劣之处。

表2是应用如上两种方法进行最优潮流计算的结果。由表2可知,在优化结果方面,高斯罚函数略优于二次罚函数。在优化求解过程中,嵌入高斯罚函数与嵌入二次罚函数的迭代次数几乎相同,但嵌入高斯罚函数计算时间更长,这是由于高斯罚函数是高阶函数,海森矩阵是非定常矩阵,每次迭代都要重新计算,从而增加了计算时间。

表2 优化结果对比Table 2 Comparison of optimization results

附录A图A4为预估—校正原对偶内点法中嵌入二次罚函数和高斯罚函数的对比,由图可知,随着迭代次数的增加,对偶间隙逐渐减小,当两种罚函数的收敛效果都达到期望值时,方法A计算时间约是方法B的1/5。

3.3 加入调压器的最优潮流二次迭代优化控制

为验证调压器对配电网节点电压分相微调,可在最优潮流计算中进一步优化目标函数值的作用,应用含有调压器的IEEE 13节点三相配电系统进行最优潮流二级迭代优化计算,计算结果见表3。

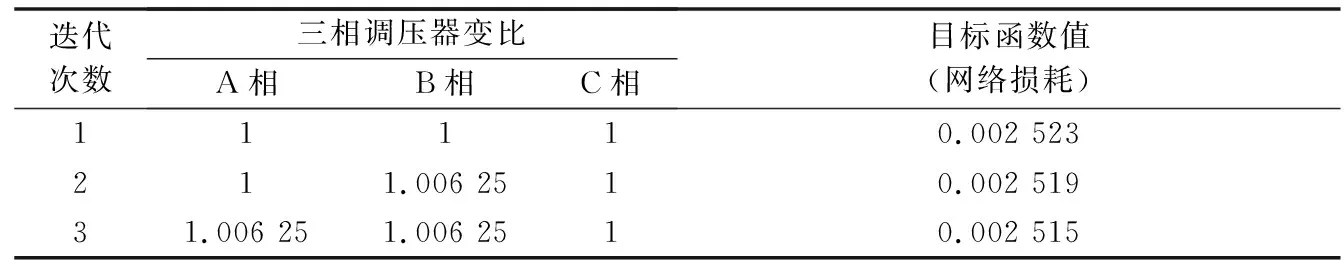
表3 含调压器的最优潮流Table 3 Optimal power flow with voltage regulator

每次迭代代表进行一次最优潮流计算和一次调压器分接头挡位计算。如表3所示,进行3次迭代后,负荷中心的电压变为规定范围内,目标函数值较没有加入调压器时减少0.32%。加入调压器后,网损减小值比较微小,这是因为调压器主要起到分相微调电压的作用。迭代前后各节点A相电压分布见附录A图A5,图中画出了节点0,1,2,3,4,5,6,7,8,11,13共11个节点的A相电压。由此可见,调压器对各节点电压有微调作用。综上可知,在最优潮流计算中,调压器可对节点电压进行分相微调并进一步优化目标函数值。