高光伏渗透配电网分散式最优潮流的割平面一致性算法

戴 月, 刘明波, 王志军, 谢 敏

(华南理工大学电力学院, 广东省广州市 510641)

0 引言

分布式光伏由于其节能环保、因地制宜、灵活分布的特点,逐渐成为新型可再生能源开发利用的重要方式,光伏电站和屋顶光伏在电力系统中装机容量所占的比重日益加大。分布式光伏发电一般以分散的方式在用户附近建设,一般接入10 kV及以下电压等级的配电网[1]。随着光伏等新能源渗透率的提高,传统配电网正逐步过渡为具有一定可控性的主动配电网,光伏发电等分布式电源对电力系统规划、仿真、调度和控制的影响也引起了人们越来越多的关注[2]。

与高压输电网不同的是,主动配电网的电阻往往不可忽略,因此其最优潮流(optimal power flow,OPF)必须依据交流潮流方程才能将电压、无功功率等因素考虑在内。因此,从数学上讲主动配电网的OPF问题是一个非凸的非线性规划问题。如何将该问题凸化或是将其潮流方程高精度线性化已成为研究主动配电网OPF方法的热点问题。近年来,基于凸松弛求解OPF的方法得到了广泛的关注,其中文献[3-4]基于支路潮流方程,借助分段线性化和二阶锥松弛技术,将原OPF模型转化为凸规划形式。文献[5]则将半定规划凸松弛技术应用于光伏逆变器的优化调度,并在小型社区屋顶光伏系统中得到了验证。

上述方法都是集中式优化方法,即调度中心在优化求解前需要收集全局信息,并用所收集到信息进行集中计算后,再向各个控制器下发控制指令。然而,随着接入设备的增多,集中式收集全局信息面临着通信瓶颈等问题的挑战[6]。此外,当参与优化调度的可控单元隶属于不同的主体时,收集全局信息还面临隐私保护方面的困难。在此背景下,分散式OPF应运而生,它将优化主体分开,每个主体分别进行优化,各个主体之间仅交换少量的信息。这样的优化方式在大量属于不同主体的分布式能源接入配电网的形势下有着很大的优势。

近年来,针对主动配电网/微电网分散式OPF的研究已经取得了不少的成果。文献[7]针对含有多个可控分布式电源的微电网OPF问题,利用预测—校正逼近乘子法将中央控制器和局部控制器解耦,并基于IEC 61850通信标准搭建了一个真实微电网的分布式架构。文献[8]利用稀疏性提升正则化和半定凸松弛技术将非凸的OPF模型进行凸化,并提出了两种分布式模型,一种是将电力网络和光伏逆变器分别视为独立的可控单元,另一种则将电力网络分割为独立的几个区域。文献[9]将半定凸松弛技术应用于三相不平衡微电网的OPF问题,将网络划分为几个独立的区域,借助交替方向乘子法(alternating direction method of multipliers,ADMM)实现了各区域的分散式求解。文献[10]和文献[11]分别利用ADMM实现了含风/光/柴/储的微电网[10]和主动配电网[11]的经济调度问题的分散式优化。文献[12]利用锥松弛技术对非凸的潮流方程进行凸化,结合ADMM算法提出了主动配电网无功优化问题的分散式算法,并给出了能够加速收敛的罚因子调节技术。割平面一致性(cutting plane consensus,CPC)算法[13]由于不需要上层协调器、不需要调节参数且具有良好的保密性,因此非常适合分散式优化计算。文献[14]对原始CPC算法进行了改进,减少了迭代次数和信息传递,并用四区域2298节点系统的经济调度问题证明了该方法在高压输电网上的可行性。

本文将CPC算法应用于低压配电网OPF问题的分散式求解。与文献[14]不同的是,与高压输电网相比,低压配电网的电阻电抗比较高,电阻不可忽略,因此需要采用交流潮流模型对低压配电网进行建模。首先对交流潮流方程进行线性近似,将网络中每个节点的节点电压用节点注入功率进行线性表达,将非凸的OPF问题转化为二次规划问题。再利用拉格朗日对偶松弛技术将集中式模型解耦,把网络和每一台光伏分别作为独立的代理,对每一个代理建立独立的主问题和子问题。通过在相邻代理间传递固定数目的割平面约束,在每个代理中都构建原问题的多项式外逼近问题,最终各个代理的主问题都可以求出最优拉格朗日乘子值和目标函数值。

1 配电网潮流方程的线性近似

假设配电网有W+1个节点,其中节点1与主网相连,节点W+1为平衡节点。其网络方程可写为:

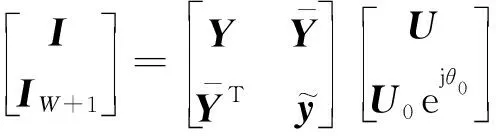
(1)

节点注入的复功率可以表示为:

S=diag(U)I*

(2)

式中:*表示共轭。

由式(1)可推导出非平衡节点注入电流表达形式为:

(3)

将式(2)与式(3)联立可得:

(4)

可以将式(4)中的电压U表示为U=Unom+ΔU,其中Unom=|Unom|∠θnom为稳态下的电压值,ΔU为系统受到扰动后稳态电压附近的偏差值。

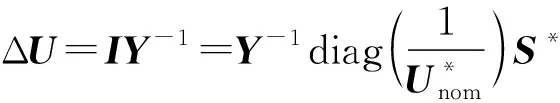
(5)

式中:Y-1为节点阻抗矩阵,由其定义可知Y-1=R+jX,其中R∈RW×W,X∈RW×W。

节点注入的复功率还可以表示为:

S=P+jQ=(Pav-Pc-Pd)+j(Qc-Qd)

(6)

式中:P为节点注入的有功功率;Pav为光伏接入节点向系统注入的有功功率,即光伏的预测出力;Pc为弃光有功功率;Pd为节点的有功功率负荷;Q为节点注入的无功功率;Qc为光伏接入节点逆变器发出/消耗的无功功率;Qd为节点的无功功率负荷。

将式(6)代入式(5),并将电压的实部和虚部分离可得:

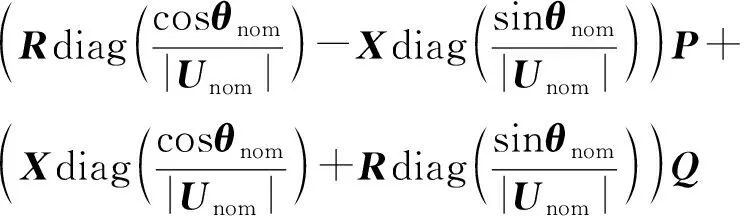
(7)

(8)

由于θnom≈0,|Unom|=1N,式(7)和式(8)可以简化为如下形式:

(9)

根据文献[15-16],电压的幅值和相角可以近似地表示为|U|=|Unom|+ΔUre,θ=θnom+ΔUim。

此节点电压的幅值和相角可以近似表达为:

(10)

式中:Rnl和Xnl分别为节点n和节点l间的电阻和阻抗;Pl和Ql分别为节点l的有功和无功功率;N′为除平衡节点外的节点的集合。

2 高光伏渗透主动配电网OPF模型

2.1 集中式优化模型

假设共有H个节点为光伏接入节点。令集合N为所有节点的集合；集合N′为除平衡节点外的节点的集合,即N′=N{N+1}；集合H表示所有含光伏接入的节点的集合；集合ε表示所有线路的集合,线路(m,n)可以表示为ε={(m,n)}⊂N×N。

1)目标函数

以最小化全网网损费用和弃光费用为目标,即

(11)

网损费用表示如下:

(Im(Um)-Im(Un))2]

(12)

式中:ymn为节点m和n间的互导纳;Um和Un分别为节点m和n的电压。

弃光费用表示如下:

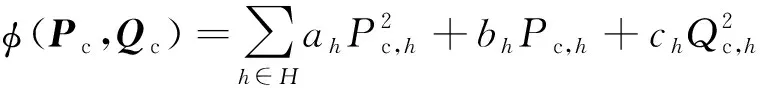
(13)

式中:ah,bh,ch为费用系数;Pc,h和Qc,h分别为节点h所接光伏逆变器的有功和无功出力。

2)网络侧约束条件

网络侧约束条件为节点电压的上下限约束。由式(9)可知,节点电压的实部和虚部可以表示为:

(14)

式中:Pav,l为节点l所接光伏的预测出力,若节点l没有光伏接入,则Pav,l=0;Pc,l和Qc,l分别为节点l所接光伏的弃光量,若节点l没有光伏接入,则Pc,l=0,Qc,l=0;Pd,l和Qd,l分别为节点l的有功、无功负荷。

因此,电压上下限约束可以表示为:

Umin≤|Un|≤Umax

(15)

3)用户侧约束条件

用户侧即为光伏接入节点侧,用户侧约束条件为弃光量上下限约束:

0≤Pc,h≤Pav,h∀h∈H

(16)

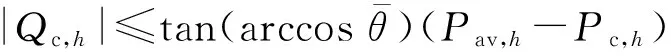
(17)

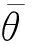
2.2 分散式优化模型

由集中式模型(式(11)至式(17))可知,可将高光伏渗透的主动配电网模型拆分成网络侧和用户侧两部分。其中网络侧由配电网的所有节点构成,其优化目标是使网损费用最小;用户侧由所有接入光伏的节点构成,其优化目标是弃光费用最小。

(18)

s.t.

(19)

(20)

0≤Pc,h≤Pav,h∀h∈H

(21)

(22)

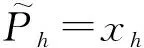
(23)

xh=Pav,h-Pc,h-Pd,h∀h∈H

(24)

(25)

yh=Qc,h-Qd,h∀h∈H

(26)

进一步将式(18)至式(26)写成如下紧凑形式:

(27)

定义耦合约束式(23)和式(25)相对应的拉格朗日乘子分别为π1,h和π2,h,用向量表示为π1和π2。通过拉格朗日对偶松弛算法,可以将式(27)转化为其对偶问题:

(28)

引入两个新的变量Lu和Lc,h表示最小化网络侧和用户侧的拉格朗日函数,式(28)可以写为如下形式:

(29)

3 CPC算法应用于求解分散式OPF问题

3.1 基本原理

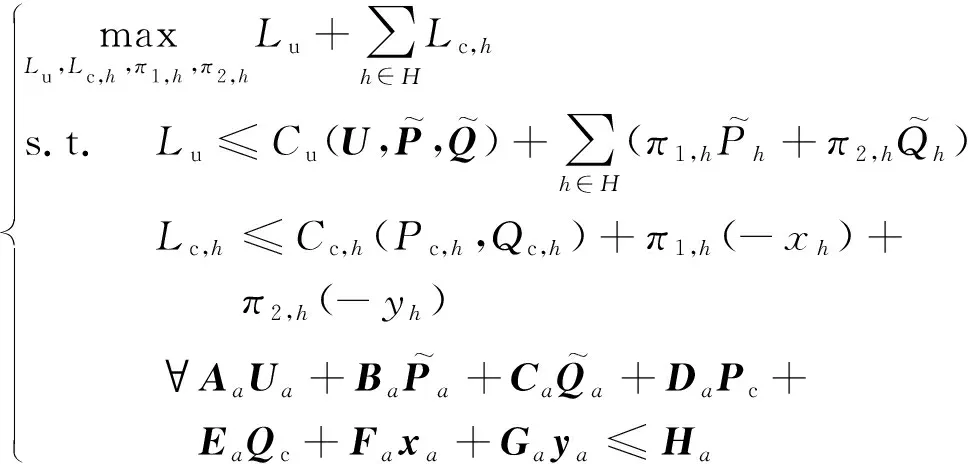
(30)

CPC算法[13]的基本思想是:对每个代理构建一个松弛了的主问题(式(30)),作为对式(29)的近似。在代理间传递少量信息,每个代理独立求解,最终每个代理都能一致地求出原问题的最优Lu,Lc,h和最优拉格朗日乘子π1,h和π2,h。主问题的形式如下:

(31)

式中:e为元素均为1的列向量;Mu,Ih,Jh,Nh,Oh,Rh均为割平面的系数。式(31)是线性规划问题,其约束条件为各个代理产生的割平面约束,它们是式(30)约束条件的线性外逼近。

每个代理的主问题当中的割平面有两个主要来源,一是利用本代理的信息产生,二是由其他代理传递而来。每次迭代在不同代理之间传递少量割平面,每个代理求解自己的主问题(式(31))。迭代结束时,各个代理都可以获得原问题的最优Lu,Lc,h和最优拉格朗日乘子π1,h,π2,h。进而网络侧可以得出保证配电网安全稳定运行前提下的最小网损,用户侧可以得出光伏的最优实际出力。算法框图如图1所示,由算法流程图可知,CPC算法不需要上层协调器,是完全分散式算法。

图1 CPC算法的框图Fig.1 Framework of CPC algorithm

3.2 割平面的产生

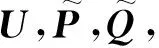
(32)

(33)

(34)

(35)

在迭代过程当中,如果主问题所求出的解不是式(30)的可行解,则各个代理都会产生各自的割平面。由式(24)和式(35)可知,割平面当中的变量仅包括该代理的La和该代理相关的拉格朗日乘子π1和π2。但是如果各代理主问题当中只包含自己产生的割平面,则最终求得的解只会满足此代理的约束条件。由于求解结束时各代理应可以得到一致的最优解,为达到这个目的,需要在不同代理间传递割平面。

3.3 割平面的传递

假设模型中一共有m个代理,由于各代理在迭代结束时可以一致获得最优解,每一次迭代过程中,代理a的主问题当中除了包含自己产生的割平面外,还应包含由其他m-1个代理产生的割平面。如果将割平面的传递方向用有向图来表示,每个节点代表一个代理,有向边代表割平面传递的方向,那么这个有向图需要满足:任意一对节点(i,j)之间都存在一条有向路径可以从i指向j,而且每次迭代时传递的方向都可以改变。以五区域为例,图2当中的三种方式均可作为割平面的传递方向。割平面的传递方向与代理之间是否有物理连接线无关,即通信线路与输电线路分离。即使两代理间存在物理连接线,只要能够通过其他代理实现割平面在两个代理间的相互传递,那么就没有必要在这两个区域之间直接传递信息。本文中,由于接入配电网的光伏分布较为分散,用户侧的代理之间传递信息难以实现,因此本文采用图2中的第一种信息传递方式,即以网络侧为通信中心与各用户侧代理相连,用户侧各代理均只与网络侧代理通信,而用户侧代理之间互相不传递信息。

图2 5区域系统的信息传递图Fig.2 Information transfer diagram of 5-area system

如果在传递的过程当中出现了割平面丢失,问题仍然可以收敛,这是因为割平面是线性约束,随着主问题当中的约束条件增加,式(30)的解域将被收紧。当发生割平面丢失时,只要有新的割平面传递进来,那么该代理的主问题就可以产生新的拉格朗日乘子解,并在满足割平面产生条件时产生一个新的割平面。这个割平面与没有割平面丢失时产生的割平面不相同,但是本质上都是对式(30)的约束条件的近似,只是逼近的程度有差异,对解域的收紧程度不同。但随着迭代的进行,各个代理总是能够生成更紧的割平面,问题最终仍然能够收敛到全局最优解。

3.4 求解步骤

(36)

式中:M为非常大的正数,如M=106。

2)按照有向图的顺序,对每一个代理a重复如下步骤。

①接收从上个代理传递而来的割平面,添加到本代理的主问题当中。

⑦将割平面传递给下一个代理。

3)收敛性判据:若式(37)或式(38)满足,则认为程序收敛,否则k=k+1,进入2)。

(37)

(38)

4 算例分析

本文算法在MATLAB 和GAMS23.95平台上实现,调用CPLEX求解器求解二次规划模型。计算机采用Intel(R) Core(TM) i5-4570处理器,内存为16 GB。

4.1 潮流方程线性化近似准确性验证

为了验证第1节所述潮流方程线性近似模型的准确性,本文在IEEE 33节点系统[17]的基础上进行了验证,对比了潮流方程线性近似前后所计算出的节点电压的实部和虚部。

IEEE 33节点系统接线图见附录A图A1。分别用非线性的潮流方程和线性近似后的潮流方程计算节点电压,所得的节点电压的实部和虚部的对比结果如图3所示。可以看出用第1节中的线性化方法将潮流方程线性化后所计算出的电压幅值和相角偏差很小,因此可以认为本文的潮流方程线性化方式是准确的。

图3 潮流方程线性化结果对比Fig.3 Comparison of linearization results for power flow equations

4.2 CPC算法有效性验证

为了验证CPC算法在主动配电网当中的有效性,本文对屋顶光伏系统[18]和含15台光伏接入的IEEE 33节点系统进行了计算。

采用3个指标来对比本文使用方法与集中式方法的结果,从而验证CPC算法的正确性。这三个指标分别是:相对目标函数值偏差δf、光伏接入节点弃光量偏差δPc和δQc。

(39)

4.2.1在屋顶光伏系统上的测试结果

小型社区屋顶光伏系统的各项参数与文献[18]一致,节点负荷和屋顶光伏预测出力数据采用某实际微电网中的负荷和光伏预测出力数据,接线图见附录A图A2。

该系统有19个节点,其中节点19为与主网连接节点。其功率基准值为1 MVA,电压基准值为240 V。其中节点1,3,6,12,15,16接入的光伏预测出力为7.7 kW;节点4,7,9,10接入光伏的预测出力为9.4 kW;节点13,18上接入的光伏预测出力为22 kW;系统的光伏渗透率为94.46%,电压上、下限分别为1.042(标幺值)和0.917(标幺值)。

屋顶光伏系统的信息传递图见附录A图A3,其中配电网为网络侧代理,12台光伏分别为独立的用户侧代理,用户侧各代理均只与网络侧代理通信。定义cu,m,n为网络侧代理u在第m次迭代时产生的第n个割平面,cch,m为用户侧代理h在第m次迭代时产生的割平面。第1次迭代开始后,网络侧代理u产生割平面cu,1,1并添加到其主问题当中,然后传递给用户侧代理1的主问题。用户侧代理1产生割平面cc1,1,并将新产生的割平面cc1,1传给网络侧代理u。此时网络侧代理u再产生一个割平面cu,1,2,并将最新产生的割平面cu,1,1,cc1,1和cu,1,2一起传递给用户侧代理2。用户侧代理2产生割平面cc2,1,并将新产生的割平面cc2,1传给网络侧代理u。以此类推,每次迭代用户侧代理只产生1个割平面,而网络侧代理可以产生12个割平面。用户侧代理在每次迭代过程当中仅传递自身新产生的割平面给网络侧代理,而网络侧代理将用户侧代理主问题中没有的、最新产生的割平面全部传递给用户侧代理。网络侧代理u可以向任一用户侧代理传递信息,但不论其向哪个用户侧代理传递割平面,均采用上述规则。由于网络侧代理的耦合约束多、与各个用户侧代理的耦合程度高,同时节点数目多、运算规模大,因此在算例中运算时间主要由网络侧代理的收敛速度决定。采用这种信息传递方式,当有n个用户侧代理时,网络侧代理的主问题每次迭代可以产生n个割平面,有助于提高运算速度。

表1列出了改进CPC算法的优化结果,可以看出采用改进CPC算法能确保收敛到正确的结果。表1同时列出了采用ADMM算法时的计算结果,由于ADMM需要对参数进行调节由于ADMM计算结果与参数取值有关,故列出了不同β取值下的计算结果,并选取其中最精确结果(β=2 500)的电压幅值、相角值与CPC的计算结果进行对比。

表1 屋顶光伏系统计算结果Table 1 Results of rooftop photovoltaic system

由表1和图4可以看出,ADMM与CPC在计算结果精度方面相差不大,当选取的β参数比较合适的时候,ADMM在计算速度方面比CPC占优。但CPC只需要传递割平面信息即可,因此CPC的保密性更强。同时由表1可以看出,ADMM的计算结果受β参数影响较大,而CPC不需要对算法参数进行调节。

综上所述, CPC的主要优势体现在:①收敛可靠;②不需要调节优化参数;③不需要交换边界信息,保密性好。

4.2.2在33节点15台光伏系统的测试结果

含15台光伏接入的33节点系统见附录A图A4,在33节点标准系统基础上,在节点3,5,7,9,12,14,17,20,22,23,25,27,29,31和32接入光伏。IEEE 33节点系统的功率基准值为1 MVA,电压基准值为12.66 kV,下文中讨论的数据均为标幺值。节点3,7,17,23,31接入的光伏预测出力为5 kW;节点5,9,12,20,22,25,27,29,32接入光伏的预测出力为22 kW;节点14接入的光伏预测出力为 95 kW,系统的光伏渗透率为85.6%。电压的上、下限分别为1.042和0.917。

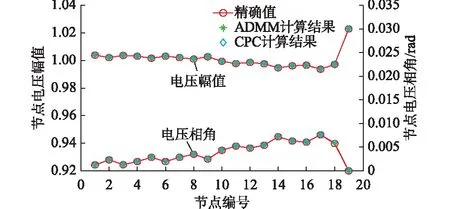
图4 屋顶光伏系统节点电压对比Fig.4 Comparison of voltages of rooftop photovoltaic system

表2列出了改进CPC算法的计算结果,可以看出不论D值的取值为多少,CPC算法均能收敛到非常相近的解,所需要的迭代次数也基本相同,这说明D值的选取对算法的收敛性影响很小。

表2 由改进CPC算法求得的33节点15光伏系统结果Table 2 Results of 33-node with 15 photovoltaic distribution network using modified CPC

附录A图A5为D=30时集中式与分布式求得的节点电压实部、虚部的对比图,可以看出二者的偏差很小,说明集中式与分布式求得的电压相角与幅值基本相同,可以说明改进CPC算法的准确性。

图5是33节点系统的收敛曲线,其中蓝色线为网络侧代理的收敛曲线,彩色线为15个用户侧代理的收敛曲线。以代理6为例,可以看出用户侧代理在迭代初期快速收敛,并在满足收敛条件的范围内波动。而网络侧代理的对偶间隙在迭代初期下降很快,但到达一定迭代次数以后呈锯齿形缓慢下降,因此主要计算时间由网络侧代理决定。本文采用的通信方式在每次迭代时,网络侧代理可以产生15个割平面,如果每次迭代令网络侧仅产生1个割平面,则计算时间大于1 h,由此可知,本文采用的通信方式可以大大提高计算效率。

图5 33节点系统迭代过程Fig.5 Iteration process of 33-node system

在传递信息时出现割平面丢失时算法仍然能够收敛到非常准确的结果。本文在15台光伏接入的33节点系统基础上模拟通信中断的过程,每次任选一个或多个用户侧代理在连续50次迭代过程中不传递割平面给网络侧代理,并对其余代理收到的割平面产生影响。附录A表A1给出了5次模拟结果,每次模拟不同代理停止传递割平面的时间不一样,迭代次数与计算结果也不同,但不管经过多少次迭代,每次模拟最终都能得到与集中式优化非常接近的结果,这说明改进CPC算法在遇到割平面丢失时仍能收敛。

5 结语

本文采用CPC算法对高光伏渗透的主动配电网的OPF问题进行分散式求解。每个代理均构建本区域的主问题对原问题进行近似,不同代理之前仅传递割平面约束,不需要上层协调器,并且不需要对步长等参数进行调节即可收敛。本文分别对屋顶光伏系统和15台光伏接入的33节点系统进行分析表明:①对于不同规模、不同光伏渗透率的系统,本文方法均可不调试参数直接得到与采用集中优化方法非常接近结果;②本文方法采用的通信方式以及采用的删除冗余割平面策略可以减少每次迭代时传递的割平面数目,大大提高计算速度;③本文所用的方法仅在代理间传递割平面信息,保密性很好。同时如果出现割平面丢失的情况依然能够收敛到正确的结果。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。