空间多层次误差移动平均模型的广义矩估计——基于广东省产业知识溢出三维非平衡面板数据

叶倩婷，龙志和（博士生导师），吴 梅（副教授），陈青青（博士）

一、引言

经济管理研究中的数据常呈现层级结构分布，数据层级间相互嵌套、相互作用，被称为层级数据[1][2]；层级数据包含了经济管理研究中常用的面板数据，对面板数据维度作了进一步延伸。常见的面板数据空间模型主要关注数据的空间特性，却未考虑数据的层级结构以及层级间的嵌套关系。

为深入挖掘层级数据的内在规律，需要进一步拓展空间多层次计量经济学模型，即同时考虑研究对象层级间的嵌套关系和层级数据的空间相关关系，以及多层次模型误差项的空间相关性，建立并研究空间多层次滞后模型和空间多层次误差模型及其衍生结构组合模型。现有文献中，对空间多层次计量经济学模型研究得并不多。Corrado和Fingleton[3]探索性地提出了空间多层次计量经济学模型的结构，但未对其具体的参数估计方法做深入讨论。在层级数据空间计量模型参数估计方面，Baltagi等[4]提出了空间多层次滞后（HSLAG）模型，并使用工具变量法（IV）以及两阶段最小二乘法（2SLS）对模型的参数进行估计；叶倩婷、龙志和[5]使用广义矩（GMM）估计法和可行的广义最小二乘法（FGLS），对空间多层次误差自回归（HSEAR）模型的参数进行了估计；随后，Fingleton等[6]把HSEAR模型用于分析英格兰房价的空间关系与层级嵌套关系。

然而，对于空间多层次误差模型而言，HSEAR模型在考察层级效应的基础上仅关注邻接地区数据误差的空间自相关关系，该如何同时考虑层级效应以及衡量地区自身所受到的空间误差冲击呢？这就需要对误差项进行高阶自回归。当自回归过程阶数提高，为减少待估参数的数量，移动平均过程的存在显得尤为必要。空间多层次误差移动平均（HSEMA）模型该如何建立，其参数该如何估计，模型可以如何应用，均为本文需展开研究的内容。

模型建立方面，由于层级数据存在层级嵌套关系，本文将以空间误差移动平均（SEMA）模型为基础，将嵌套误差项引入SEMA模型，构建HSEMA模型。模型参数估计方面，Fingleton、Le Gallo[7]推导了截面数据SEMA模型可行的广义空间两阶段最小二乘（FGS2SLS）估计，并指出SEMA模型估计量的推导与SEAR模型有许多相似之处，但在其细节与意义上有很大的区别。本文参考Fingleton[8]对面板SEMA模型参数的GMM估计方法，对HSEMA模型参数进行估计。HSEMA模型可以同时衡量研究对象自身的误差冲击效应，并考虑数据层级结构，进而对其产生的空间误差移动平均系数和层级效应进行有效测量，填补当空间多层次误差模型的误差项存在移动平均结构时，其估计方法的空白，以期推进空间多层次模型的理论研究。进一步，在模型应用方面，采用2005～2013年广东省21个地级市所具有不同数量工业产业的“时间—地区—产业”三维非平衡面板数据，同时考虑数据中的层级嵌套效应与空间溢出作用，对产业间知识溢出效应进行实例分析。

二、空间多层次误差移动平均（HSEMA）模型

空间多层次误差移动平均（HSEMA）模型构建思路如下，参考前人对HSLAG和HSEAR模型的研究[4][5][9]，以测量时间—地区—产业（此层级亦可为省、市、县）三维数据为例，建立HSEMA模型：

其中：i=1，…，N；j=1，…，mi；t=1，…，T；记yijt为t时期i地区j产业因变量的观测值；xijt为一个1×K维观测向量；β是一个K×1维参数向量；uijt为t时期i地区j产业的误差项；εijt为t时期i地区j产业的由于未被考虑到的变量所引致的新息误差，且具有误差分量结构；θ是空间误差移动平均系数，衡量在j点自身的误差冲击效应大小，它只影响在空间权重矩阵非零元素对应的产业间有直接相互作用的位置，这样的冲击效应为局部的空间相关性；两个层级随机效应误差分量结构αi和μij分别代表地区随机效应，以及第j个产业嵌套于第i个地区中的嵌套随机效应；νijt为其他误差冲击因素。HSEMA模型设定与估计的前提假设与HSEAR模型类似。此外，这个模型允许每个地区的产业数量不相等，地区间可以有不同数量的观测时期，即适用于非平衡面板数据。

模型（1）可转换为矩阵形式：

其中：y为TS×1维向量；X为TS×K维观测矩阵，假设X为列满秩且其元素绝对值一致有界；β的维度为K×1，u的维度为TS×1；αT=（α1，…，αN），μ是S×1维向量，ν与u类似定义；lT为T×1维全1列向量；W=IT⊗WS，⊗为克罗内克积，WS是一个已知的S×S维空间权重矩阵，且主对角线上元素为0，WS由 N2个子矩阵组成，WS=［Wig］，其中 i、g=1，…，N ，其子矩阵Wig的维数为mi×mg，即Wig=［ωij，gh］，其中j=1，…，mi，h=1，…，mg；ITS=IT⊗IS为TS×TS维单位矩阵，（ITS+θW）为TS×TS维非奇异矩阵，且|θ|＜1成立。

因为E［u］=0，误差项u的方差协方差矩阵为：

其中，由于ε的误差分量结构与HSEAR模型的设定相同，故ε的方差协方差矩阵Ωε和与HSEAR模型一致。

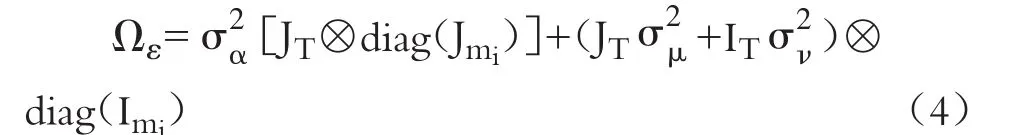
经谱分解后，方差协方差矩阵Ωε的逆可表达如下：

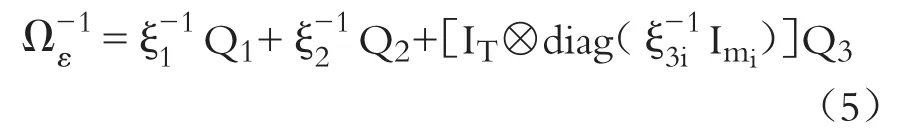
三、广义矩（GMM）估计

本文借鉴Kapoor等[10]与Fingleton[8]的GMM估计研究框架，推导HSEMA模型的矩条件，据此定义其参数的最优权重GMM估计量。区别于HSEAR模型，推导HSEMA模型矩条件主要涉及、、。为了计数方便，令：

为了得到这些变量的期望，对2≤T≤∞求得18个矩条件，如表1所示。

那么由式（2）和（6）可得：

对∀i=1，2，3，左乘Qi至式（7）有：

不难得到以下二次型：

将矩条件代入式（9），记：

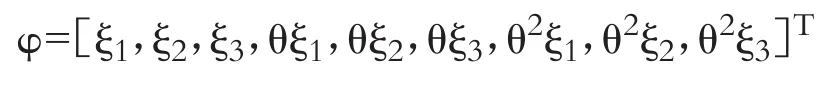
得到包含参数θ、ξ1、ξ2和ξ3的矩函数体系：

由辛钦（Wiener-khinchin）大数定理，只要样本容量达到充分大，样本矩收敛到总体矩的概率等于1。令为β的一致估计量，则：

令参数向量为ψ=（θ，ξ1，ξ2，ξ3），且ψ∈△，其中△=［-a，a］×［0，b］×［0，c］×［0，d］，a≥1，b≥bν，c≥式（11）对应关于和的样本形式为：

这里ς（ψ）是一个残差向量。

显然，式（10）中的前三个等式与ξ2和ξ3无关，后六个等式与ξ1无关 。令可改写为：

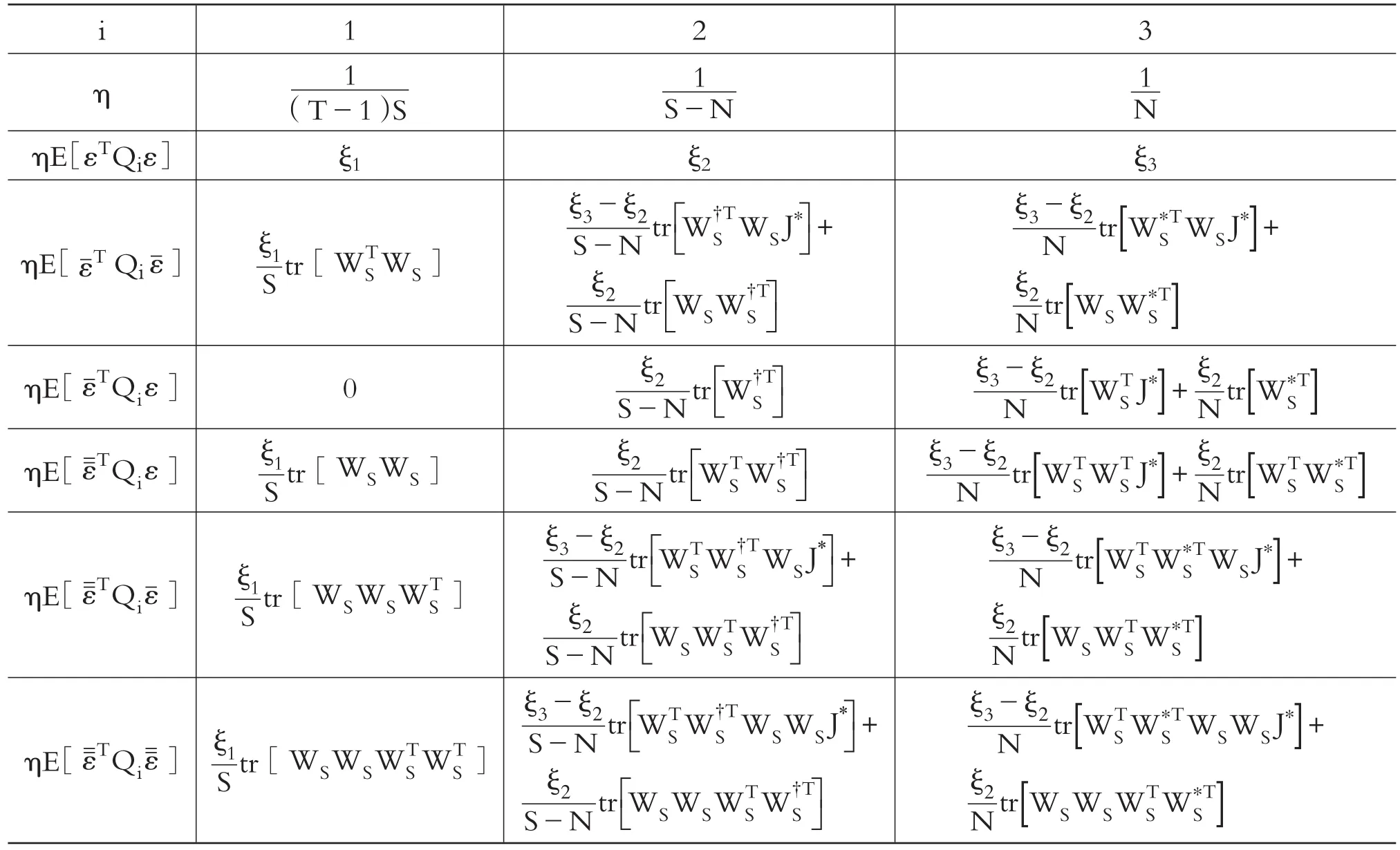
表1 HSEMA模型矩条件

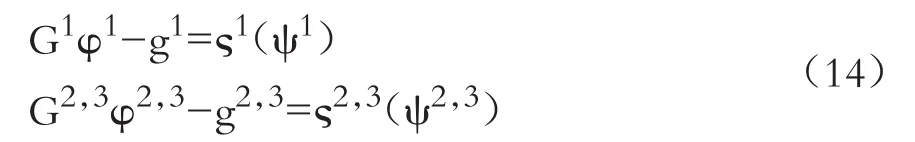
基于GMM估计的基本规范与论述[11][12]，采用矩条件的方差协方差矩阵构建最优权重矩阵，从而得到渐近有效的GMM估计量，将样本矩之间的加权距离最小化。那么最优权重GMM估计量定义为：

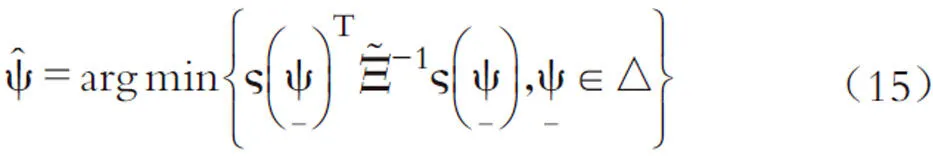
此处要求参数空间△为紧集，从而保证GMM估计量的一致性。

由于模型误差项ε的方差协方差矩阵Ωε不是常数，式（2）中总体回归系数β的广义最小二乘（GLS）估计量为：

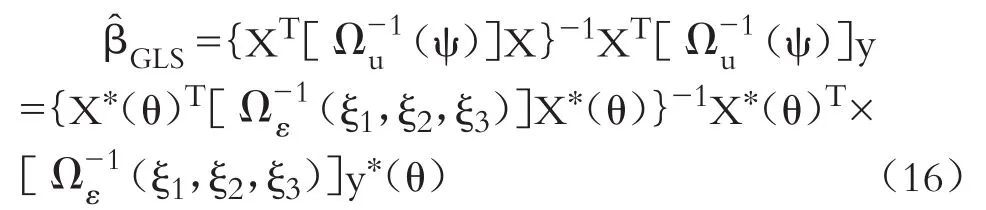
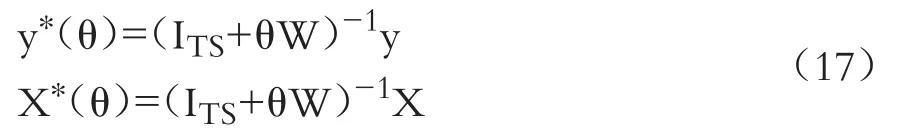
变量y∗（θ）和X∗（θ）可看成原始模型（2）的空间科克伦—奥克特变换。

四、基于HSEMA模型的广东省工业产业知识溢出实例分析

“粤港澳大湾区”已经上升到我国经济发展的核心战略地位。本文以三维非平衡层级数据为例，对广东省工业产业知识溢出效应进行研究。由下图可以看出广东省技术密集型产业工业增加值占比均超过50%，且逐年递增，说明广东省工业产业结构以技术密集型为主导。弄清广东省是否存在知识溢出效应且为何种知识溢出效应，对“粤港澳大湾区”经济发展规划意义重大。

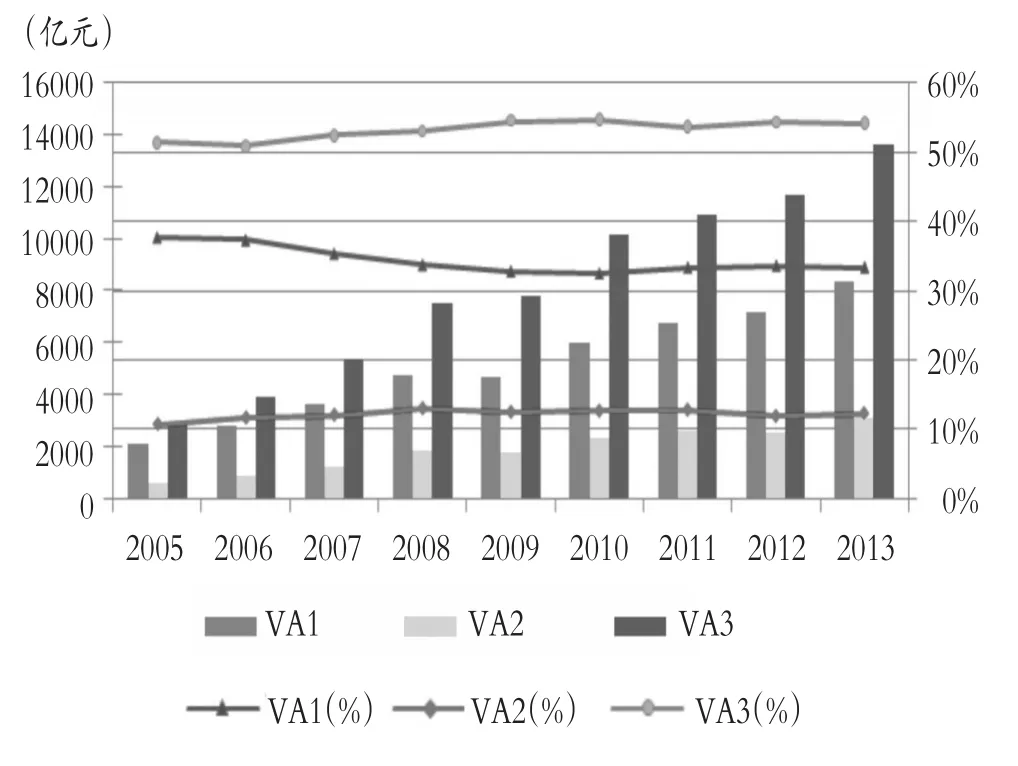
2005～2013年广东省按资源密集度分类工业增加值图

有关工业产业的知识溢出效应，国内外学者依据不同地区、不同时期的数据做了大量研究[13][14]，研究产业经济增长是如何受知识溢出影响的[15]。然而，已有研究未同时考虑数据间存在的空间效应和层级结构，可能对知识溢出程度的估计产生偏差。广东省经济总量以及GDP增速等主要经济指标均位居各省前列，对全国的经济增长有重要的支撑和标杆作用。实际经济管理数据经常为“多维度”“不完整”的非平衡数据，为了进一步考察工业产业的知识溢出效应对经济的影响，采用HSEMA模型，使用广东省9个年度、21个地级市所具有不同数量工业产业的三维非平衡面板数据进行实例分析。

本文所需数据取自2006～2014年《广东统计年鉴》和《广东工业统计年鉴》，所选取产业类别参考国家统计局2002年对工业产业的分类。

考虑数据的层级结构和空间效应，考察工业产业知识溢出效应对经济增长的作用。此处采用Cobb-Douglas生产函数，令第“t年—i地区—j产业”的工业增加值为模型的因变量，技术水平、劳动力和物质资本投入为自变量：

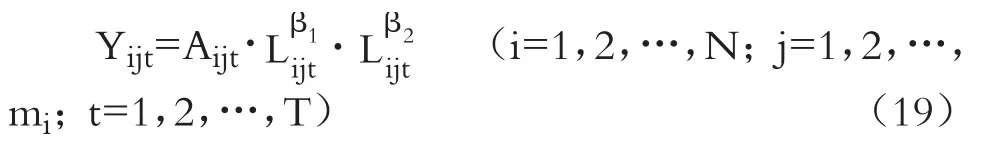
其中，i代表第i个地区，j表示第j个产业，t代表时间，采用频度为年的数据。Y代表工业增加值，A代表技术水平，L为劳动力投入，K为物质资本投入。为便于估计和消除量纲影响，对方程（19）两边取对数，得到以下模型：

对方程（20）中的技术水平A进行分解，包括以下三个外溢指标：MAR外溢（某地区专注于某一类产业的专业化生产能促使该地区经济增长）、Jacobs外溢（地理位置邻近的地区产业多元化比产业结构单一更能促进产业创新和经济增长）和Porter外溢（产业间的相互竞争、优胜劣汰促使产业知识更新换代推动经济增长），分别代表产业专业化、多元化与竞争性外溢，用SPEC、DIV和COMP表示其变量名称。由式（1）和式（20）得到基于空间多层次误差移动平均模型的知识溢出效应实证分析基础理论模型：

其中，Yijt为t年i地区j产业的工业增加值，衡量产业的发展；Lijt、Kijt、SPECijt、DIVijt、COMPijt为 t年i地区j产业影响产业发展的要素；μij为t年i地区j产业的误差项。θ是空间误差移动平均系数，误差项εijt具有移动平均结构以及误差成分结构，αi为地区随机效应，μij为第j个产业嵌套于第i个地区中的嵌套随机效应，νijt为其他误差冲击因素。各变量意义与对应参数如表2所示：

表2 指标体系设定与预期经济意义

根据Batisse[16]和Mihn[17]的方法计算专业化指标（MAR 外溢）lnSPECijt，根据 Ellison、Glaeser[18]的方法计算多元化指标（Jacobs外溢）lnDIVijt，根据De Lucio等[19]的方法计算竞争性指标（Porter外溢）lnCOMPijt，以t年i地区j产业的工业增加值（或从业人数、企业个数）占全国该产业对应指标的比重，描述知识溢出效应（即份额相对值或比例相对值）。

使用上述2005～2013年广东省“时间—地区—产业”的三维非平衡面板数据，采用混合回归模型和面板数据SEMA模型，与HSEMA模型进行对比。对混合回归模型，若该地区无对应产业，则以空值替代，其参数使用OLS估计；根据Fingleton[8]的估计方法对SEMA模型参数进行估计；对HSEMA模型，运用本文提出的最优权重GMM估计量对其误差项标准差进行估计，进而对总体回归参数进行FGLS估计。估计运算用GAUSS 15.0软件进行编程，结果见表3。

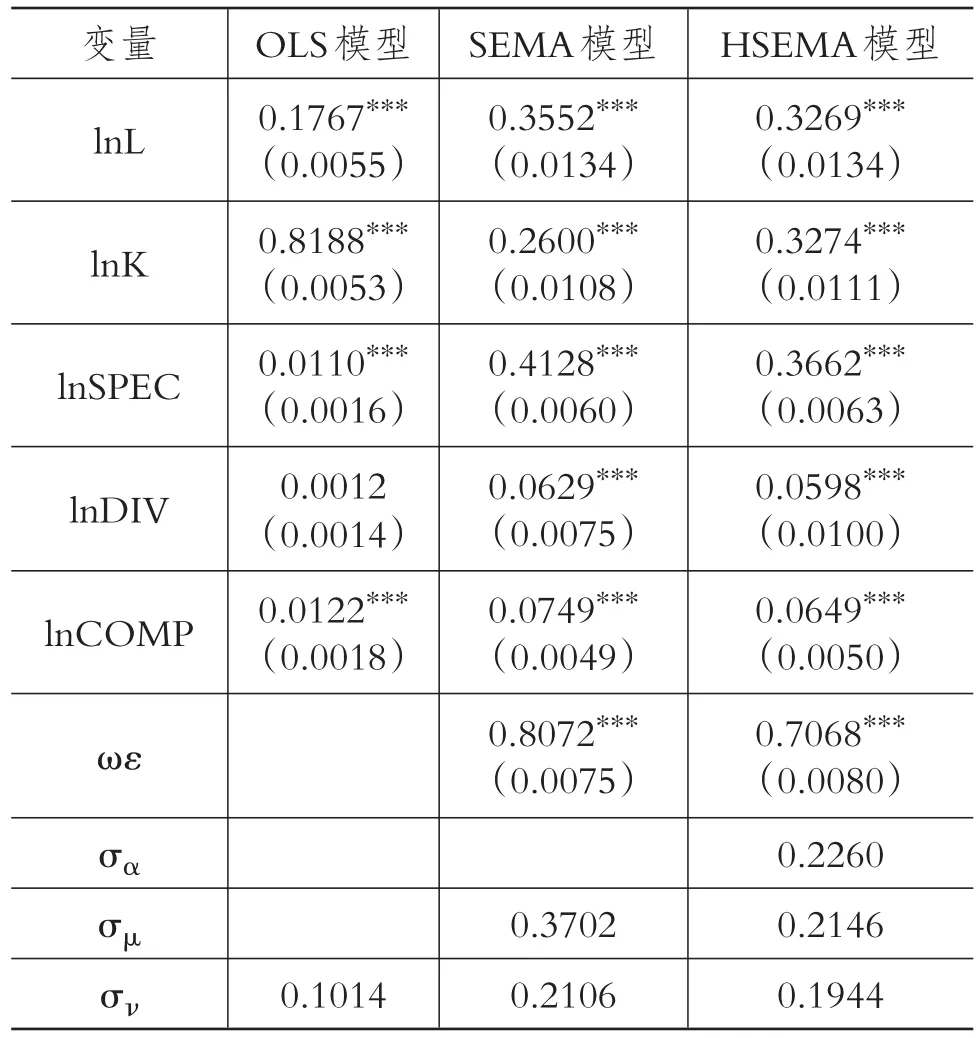
表3 空间多层次误差移动平均模型参数估计

从实证结果可以看到，混合回归模型中劳动力和物质资本投入，以及其他各知识溢出效应对工业增加值存在推动作用，OLS估计结果认为物质资本投入弹性（0.8188）的作用远超出劳动力投入弹性（0.1767），即广东工业产业发展主要依靠物质资本投入，与事实不符。变量lnDIV对应的参数不显著，说明产业多元化结构对广东省产业发展没有显著影响，其余各参数估计值均在1%的水平上显著为正值，但产业专业化和竞争性溢出弹性估计值分别为0.0110和0.0122，即广东省工业产业专业化程度与竞争对工业增加值影响甚微，此结果与广东省的技术密集型特征明显相悖。混合回归模型单纯地将9个年度广东省所有地区的数据一起回归，核心变量lnL和lnK的方差膨胀因子（VIF）均大于10，有较严重的多重共线性，而且忽略了数据的时间跨度、层级特性与空间溢出作用，造成过度拟合、最小二乘估计结果与现实背离，导致回归结果失真。

从SEMA和HSEMA模型估计结果可知，模型考虑数据中的时间跨度与空间效应，其参数估计值都在1%的水平上显著为正，劳动力投入弹性分别为0.3552和0.3269，物质资本投入弹性分别为0.2600和0.3274，MAR外溢弹性分别为0.4128和0.3662，Jacobs外溢弹性分别为0.0629和0.0598，Porter外溢弹性分别为0.0749和0.0649。这说明本文所列出的各项指标均对工业增加值具有促进作用，不同于混合回归模型，产业专业化、多元化与竞争性给广东省的工业发展带来显著正向影响，与表2预期经济意义一致。劳动力投入弹性和各项知识溢出弹性显著提高，物质资本投入弹性大大降低，表明当模型考虑空间相关性的影响时，劳动力投入和一定程度的知识溢出对产业经济增长的贡献作用增大，劳动力和物质资本的跨区域流动因素、产业专业化、多元化以及竞争外溢得以体现。

对于空间相关性的评估，SEMA和HSEMA模型衡量一个地区产业内部误差冲击效应的空间误差移动平均系数θ分别为0.8072和0.7068，说明一个地区产业中具有非常强的局部空间相关性，某一产业受到其过去以及该地区内部各产业未被考虑到的新息冲击效应的影响较大。HSEMA模型在考虑空间相关性的基础上同时考虑数据中的层级结构，θ的估计值与SEMA模型相比有所降低，空间误差移动平均系数θ、劳动力投入、物质资本投入和知识溢出指标弹性均得到修正。

此外，SEMA模型给出了衡量所有地区全体产业随机效应的标准差（波动率）为σμj=0.3702。HSEMA模型给出了衡量地区间的差异程度的地区层级随机效应标准差为σαi=0.2260，以及考虑产业嵌套于地区中，衡量产业间的差异程度的产业嵌套随机效应的标准差为σμij=0.2146，说明地区随机效应差异程度和嵌套随机效应差异程度可被识别。可以发现，当考虑数据层级结构的影响，σμij＜σμj，按地区分组后组内产业差异程度σμij较所有地区全体产业混合的产业差异程度σμj下降，即组内相似性得到提高，使得SEMA模型在一定程度上得到修正。不难看出，采用同时考虑空间误差移动平均和嵌套随机效应的HSEMA模型更好，模型估计结果更为符合经济现实。

使用HSEMA模型对广东省工业产业知识溢出效应的实证研究发现，劳动力和物质资本投入、产业专业化、多元化以及竞争外溢对产业发展起到正向促进作用，且具有相当强的产业局部空间相关性。在研究对象存在层级结构与空间相关的情况下，与SEMA模型相比，HSEMA模型能识别地区间差异，并进一步修正产业间差异。

五、结论

本文构建了可同时考察数据层级效应与空间误差移动平均系数的HSEMA模型，其误差项可以分解成两类层级随机效应，分别是地区随机效应以及产业嵌套于地区中的嵌套随机效应。基于广义矩估计框架，得出HSEMA模型的18个矩条件元素，由此得到各参数的GMM-FGLS估计量。实例分析表明，模型适用于三维非平衡面板数据，并对传统计量经济学模型的估计结果进行了修正，能更好地反映实际经济运行特征。

文章推进了空间多层次误差模型关于空间误差局部相关估计的研究，与HSLAG模型、HSEAR模型可以相互补充，完善了同时具有层级结构与空间效应数据模型的估计方法研究，为经济管理研究提供了新的研究思路。对于后续探索，可研究空间多层次模型的检验统计量；考虑数据的地理坐标，结合地理加权回归重塑空间多层次模型，对其参数估计量与检验统计量进行推导，侧重研究层级数据的空间异质性。