基于准稳态实验方法研究橡胶材料的热传导性质

周厚兵，唐 耿，张欣蕊，赵子珍，卢慧金，王乐乐

(广西师范大学 物理科学与技术学院，广西 桂林 541004)

热导率为单位温度梯度下每单位时间内由单位面积传递的热量，在生活中经常被用于比较各种材料的导热性能或判断保温性能的好坏. 热传递过程可以通过传导、对流以及辐射3种形式实现，而对于固体材料，热量主要通过热传导的方式进行传递[1]. 橡胶材料在生产生活中应用广泛，其热传导性能在化工、建筑行业、能源、动力工程、食品贮藏等实际生产生活中的很多领域具有重要意义. 同时，固体材料热导率的测量也是大学物理实验教学的重要内容之一，此类实验在国内多所高校均有开设[2-5]. 目前测定固体材料热导率的普遍方法为稳态法，即通过观测单位时间内经过单位横截面积的热量和一定厚度的材料2个侧面的温度差，进而求得该材料的热导率[6-7]. 该方法所用的仪器价格经济，操作简单. 但是，在近些年的实验教学实践中发现，采用稳态法测量物质热导率时要求温度和热流量均要稳定[5]，条件相对苛刻，而且学生实验中存在误操作等行为，导致测量结果的稳定性和一致性较差，实验精度不高. 为了克服这些缺陷，本文采用准稳态法在室温条件下测定橡胶材料的热导率, 该方法只要求实验过程中温差恒定及温升速率恒定，具有操作简便、耗时少、条件易于达到等优点. 实验通过改变不同的测量参量，找出准确测量橡胶材料的热导率的最佳实验条件.

1 实验原理及方法

1.1 实验原理

如图1所示，基于一维无限大导热模型的框架下，假设不良导体平板的厚度为2R，初始温度为t0. 实验过程中在平板两边同时施加均匀的指向中心面的热流密度qc，此时平板各处的温度t(x,τ)将随加热时间τ而发生变化. 以样品的中心为坐标原点，可得出热传导方程为[8]

(1)

(2)

图1 无限大平板两端施加均匀热流密度的物理模型图

在初始条件下：

(3)

t(x,0)=t0.

(4)

通过求解式(1)和(2)可以得出：

(5)

(6)

于是，在样品的中心位置处，x=0，得出

(7)

在样品的加热面位置处，x=R，可以得到

(8)

根据式(7)～(8)可知，若加热时间τ足够长，样品中心面和加热面的温度与加热时间将逐渐趋于线性关系，此时二者的温差可表示为

(9)

因此，根据(9)式可知样品加热面与中心面的温差为恒定值，与加热时间没有直接关系，即系统处于准稳态. 于是，样品的热导率为

(10)

1.2 实验方法

在实验室条件下，无法将待测样品尺寸做到一维无限大. 基于测量原理，采用的橡胶样品的横向尺寸将大于其厚度的6倍以上，此时可近似认为热流只沿着样品的厚度方向传播. 因此，选取了横向尺寸9 cm×9 cm且厚度为1 cm的橡胶材料作为测量样品. 为了精确地确定加热面的热流密度，实验过程中采用超薄型加热器作为热源，其加热功率在整个加热面上均匀并可精确控制，且本身的热容可忽略不计. 为了实现加热器两端具有相同的热阻，实验测量时共放置4块样品，安装方法及测量原理如图2～3所示.

图2 样品安装示意图

图3 测量原理图

根据(10)式，要得到待测样品的热导率λ，关键在于准确测量出样品中心面与加热面的温差Δt. 传统测量温度的方法一般是直接用温度计，但是会给实验引入许多不可控的测量误差. 为提高测量精度，实验采用温差电偶[9]测定样品的温度. 安装样品时，温差电偶的测温端应保证置于样品的中心位置，即图2中的样品2和样品3之间，以防止由于边缘效应影响到测量精度，加热面温差电偶应该放到样品3和样品4之间，通过调节固定旋钮压紧样品. 实验中，可通过用2个分别放置在加热面和中心面中心部位的温差电偶作为传感器准确获得被测样品的温差和温升速率.

2 实验数据及结果分析

文献[7]中虽然给出了运用准稳态方法测量固体材料热导率的实验条件，但是，该方法中需要准确测定的温度物理量对测量环境非常敏感，不同的测试条件直接影响测量结果. 因此，为了得到准确的实验结果，实验分别设定了不同的加热电压及测量时间，以便找出最佳的实验条件. 表1～3中分别给出了加热电压在16～19 V之间，测量时间间隔分别为30,60,120 s时获取到的橡胶材料的实验数据，表1中加热时间为t,温差热电势为Ut,中心角热电势为U,每min温升热电势为ΔU. 测量过程中温差电偶的冷端接入保温杯的冷水中，保证在实验时冷端具有恒定温度.

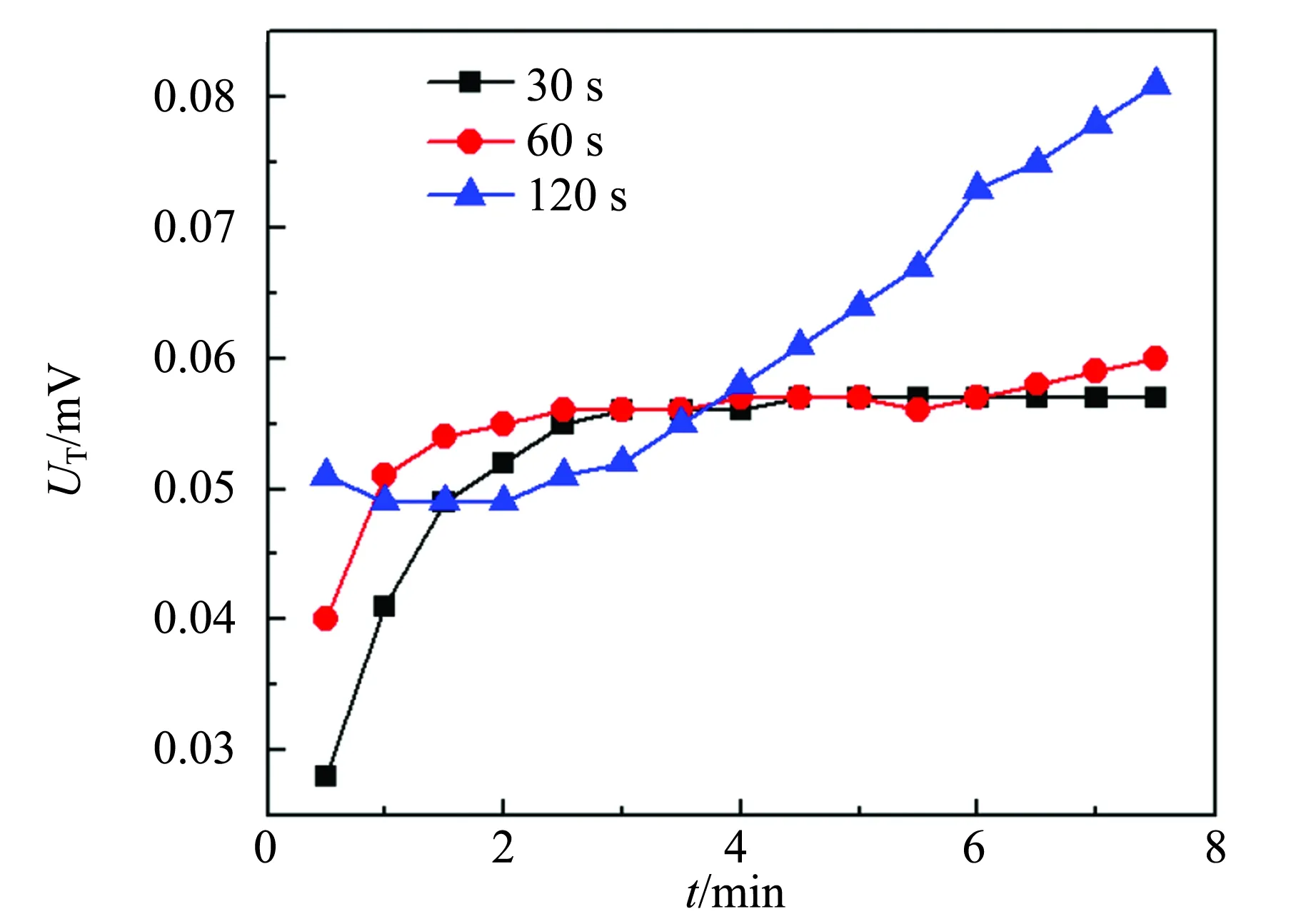
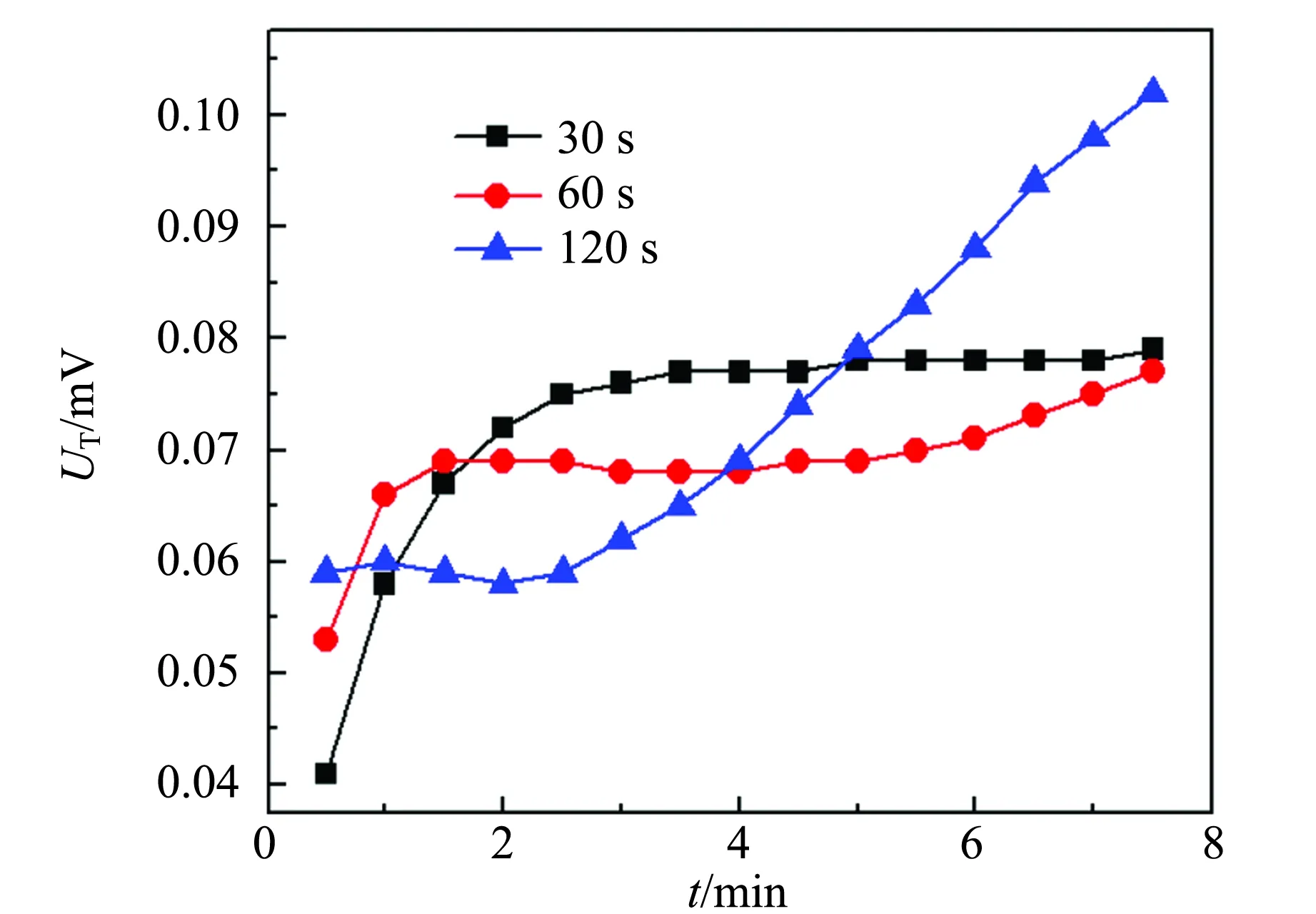
为了能直观地体现出样品中心面与加热面的温差随着加热时间的变化关系，图4中分别给出了不同测量条件下的温差变化曲线. 通过对橡胶材料的温差曲线进行分析可以发现：温差热电势总体趋势都随着加热时间的推移先急剧升高，加热到一定程度后温差热电势趋于平衡，最后又有所升高.

表1 测量时间间隔为30 s时的实验数据

表2 测量时间间隔为60 s时的实验数据

表3 测量时间间隔为120 s时的实验数据

(a)16 V

(c)18 V

(b)17 V

(d)19 V

在4个加热电压条件下，测量时间间隔为30 s时，温差热电势在加热时间4～6 min左右趋于恒定；时间隔为60 s时，温差热电势在加热时间为4～10 min趋于恒定；时间间隔为120 s时，温差热电势在加热时间为4～10 min趋于恒定. 因此，可知橡胶一般在加热时间为4～10 min时温差热电势趋于恒定，即达到准稳态的测量条件. 基于实验测量数据，利用式(10)即可以计算出橡胶热导率的测量值. 本工作中，橡胶材料样品的厚度R=1 cm，密度ρ=1.310 4×103kg/m3,加热电压U=18 V，边缘修正系数A=0.85，经修正后的加热面积F=0.006 885 m2，每个加热器的电阻r=110 Ω，铜-康铜温差电偶的热电常数为0.04 m·V/K. 本次实验中，由于直接观测量只有温差热电势1个物理量，故影响实验结果精度的主要误差来源于温差热电势的测量是否准确. 因此，运用误差传递原理得出橡胶样品热导率的测量不确定度u(λ)：

(11)

将实验数据代入(11)式，计算出测量不确定度. 计算结果如图5所示.

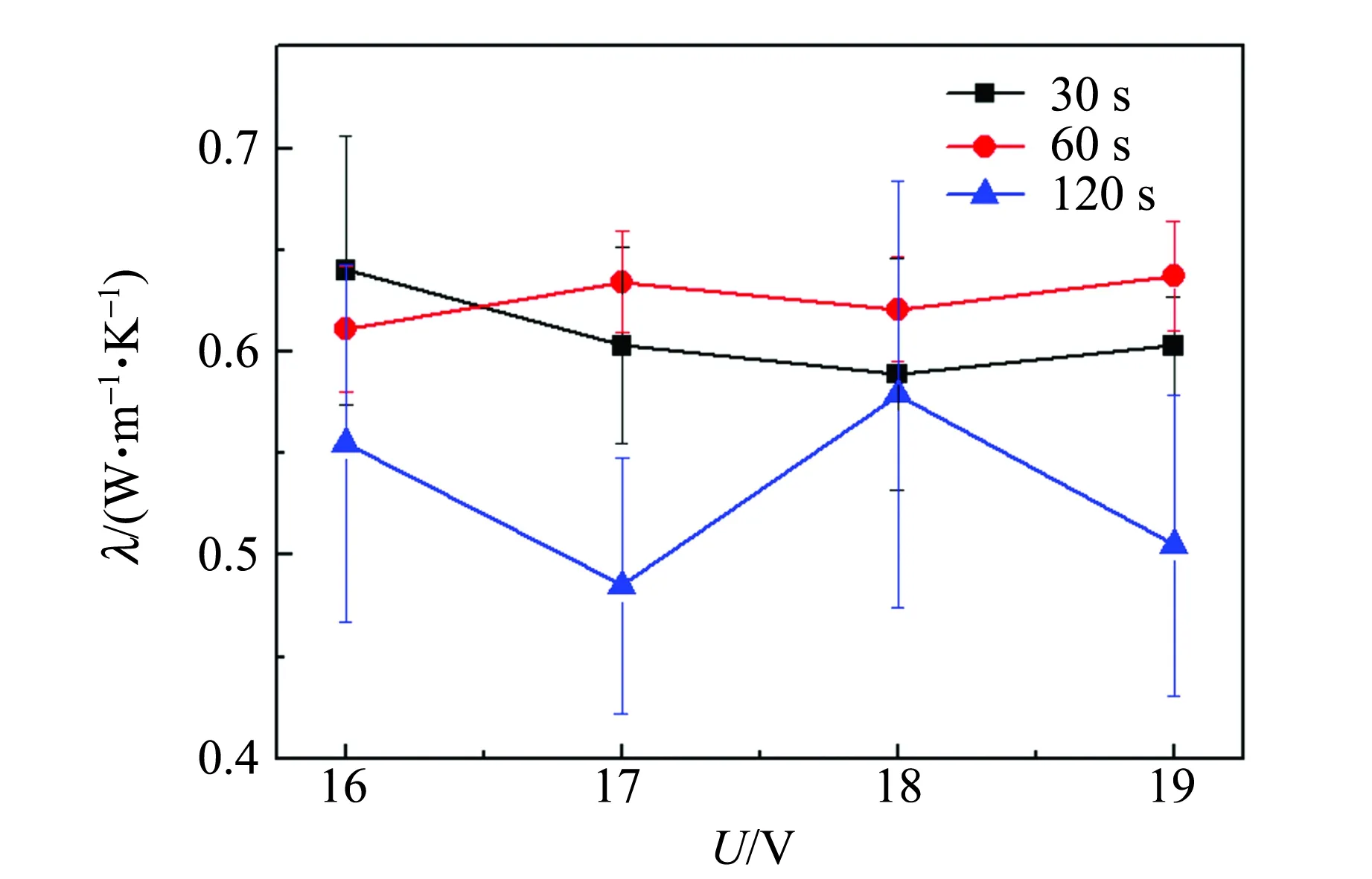
图5 不同实验条件下橡胶导热系数测量值

由图5可以看出，当测量时间间隔分别设置为30 s和60 s时，加热电压为分别为16,17,18,19 V条件下，实验所测得的热导率都比较稳定，但是在时间间隔为30 s时，在加热电压为16 V和17 V时出现较大的误差，而时间间隔为60 s时，在不同的加热电压条件下所测得的热导率误差都比较小，当测量时间间隔达到120 s时，实验所测得的热导率存在较大波动，同时也存在很大的误差. 从加热电压上分析还可以发现，当加热电压为18 V时，在不同的测量时间间隔条件下所测得的热导率都比较接近. 因此，在测量橡胶的热导率时，测量时间不宜过小或者过大，一般为60 s比较合适，同时，加热电压应设置成18 V为最佳.

3 结束语

利用准稳态方法在实验室条件下测量了橡胶样品的导热系数，由实验结果发现该橡胶材料通过加热6～10 min后系统达到准稳态状态. 最佳的实验测量条件应将加热电压设置为18 V，测量时间间隔设置为60 s时，此时得出的橡胶导热系数的测量值λ=(0.64±0.03) W/(m·K)，与本文中采用的橡胶材料的出厂推荐值λ≈0.60 W/(m·K)非常接近.

通过改变加热电压和测量时间间隔找出了橡胶材料的最佳测量条件，但是仍然有许多后续工作需要深入开展，其一是不知道在加热电压为18 V附近其他电压和其他的时间间隔所测得的导热系数是否更加准确；其二是在个别条件下，由于存在温升速率没有保持恒定的情况导致所测得的导热系数误差较大. 因此，在以后的实验中，应设置更多的加热电压和时间间隔以找到更好的实验条件，也要想办法克服温升速率不稳定给导热性能的测量带来误差这一问题.