基于随机标记子集的多标记数据流分类算法
2018-08-09孙艳歌李艳灵
孙艳歌,尤 磊,卲 罕,李艳灵
(信阳师范学院 计算机与信息技术学院,河南 信阳 464000)
0 引言
在众多实际问题中,数据都是以流的形式不断产生的.这种快速到达的、实时的、连续的和无界的数据序列称为数据流(Data Streams)[1].近年来,针对单标记数据流分类问题,国内外学者进行了广泛深入的研究.传统的单标记数据流分类算法没有充分考虑到数据流中的数据可能同时隶属于多个标记的情况,因此无法对多标记数据流进行分类.然而在现实世界中多标记数据流是非常普遍的.例如,用户可能对交叉领域的文章感觉兴趣,同时这些兴趣并不是一成不变的,如何预测用户对同时属于某些多个类别的文章是否感兴趣,这些都是典型的多标记数据流分类问题.
从学习和预测的观点来看,标记间的依赖关系是重要的信息来源,可以用于弥补待预测实例本身信息不足的缺点[2].例如,当一部电影被标有“武侠”和“古装”两个标记时,它被标记为“动作”的可能性就很高;当一则新闻被标记为“军事”时,它就不太可能同时拥有“娱乐”标记.因此,近年来大量多标记学习的研究工作都在于标记间依赖关系的发现和利用.在多数据流环境中,数据流的潜在分布会随着时间的发生变化,这使得训练数据的分布与测试数据的分布不一致,这种现象称为概念漂移(Concept Drift)[3].这使得原有的分类模型不再适用,就需要快速地检测到这种变化,并动态更新模型以适应这种改变.
本文在分析多标记数据流学习特性的基础上,提出了一种考虑标记间依赖关系的,应对多种类型概念漂移的自适应集成分类算法.本文主要贡献如下:
(1)利用集成的周期加权的机制来应对渐变式概念漂移,同时引入内部的概念漂移检测机制以增加对突变式概念漂移的适应性.
(2)提出了一种基于随机划分的标记子集的概率分类器链算法,在充分利用标记间依赖关系的同时,又有效地降低了概率分类器链的时间复杂度.
1 相关工作
近年来,研究者提出了众多的多标记分类算法,总体可以分为两类:算法适应方法和问题转化方法[4].算法适应方法是通过扩展现有的单标记学习算法,使其能直接处理多标记数据,典型的算法有基于决策树[5]、KNN[6]和神经网络的改进算法[7]等.对于不同的学习模式一般都采用不同的扩展策略,通常一种学习模型的拓展策略并不适用于其他模型.问题转化方法是将一个多标记实例集转化成一个或多个单标记实例集,从而可以直接应用已有的单标记分类模型来解决多标记分类学习问题.因此相比较下问题转化策略具有更好的灵活性.典型的问题转化方法包括基于二值的BR(Binary Relevance)转化和基于标记幂集合的LP(Labelset Power)转化.READ等[8]提出了分类器链算法,在保持了BR转化的简单有效性同时,又考虑了标记间的依赖关系.在分类器链的基础上,DEMBCYNSKI等[9]提出了概率分类器链PCC(Probabilistic Classifier Chains)算法.PCC算法从最小化损失和贝叶斯最优估计角度来解释多标记问题.
上述的多标记算法都是基于静态数据集的,无法直接应用多标记数据流环境中.QU等[10]提出MBR算法,将数据流划分成连续的数据块,在每个数据块上用BR方法转换过的多标记分类器,在分类时只保存最新k个分类器,采用集成的方式对样本进行分类.KONG和YU[11]提出了多标记数据流随机生成树算法(Streaming Multi-lAbel Random Trees,SMART),可以有效地更新模型结构和统计多标记数据流中在树的每个节点的数目,但是算法并未考虑概念漂移问题.READ等[12]提出的多标记Hoeffding树算法(Mudti-Label Hoeffding Tree,MLHT)与SMART类似,此算法是Hoeffding tree算法在多标记数据流学习中的扩展.随后READ等[13]又提出了EaHTps算法,采用自适应窗口算法作为概念检测器,当发现有概念漂移发生时建立新的分类器,使用PS算法剪枝叶子节点中不频繁出现的标记组合.SPYROMITROS-XIOUFIS等[14]用多个窗口的方法(Multiple Windows,MW)解决多标记数据流中的数据概念漂移和数据倾斜问题,由于算法需要事先对窗口参数进行设置,因此很难在实际中操作.
2 基于随机标记子集的多标记数据流集成分类算法
2.1 多标记数据流分类模型描述
设x⊂Rd为样本空间,L= {l1,l2,…,lm}为含有m个标记的标记集合.在多标记数据流学习中,数据流可表示为:
S={(x1,y1),…, (xt,yt) ,…},

2.2 基于随机标记子集的概率分类器链
为提高概率分类器链的运行效率,本文提出一种基于随机划分的标记子集的概率分类器链算法(RAndom K labelset Probabilistic Classifier Chain, RAKPCC).算法的主要思想是将原始较大的标记集随机地划分为多个较小的标记子集,并针对每个标记子集训练一个概率分类器链.当对一个未知实例分类时,使用所有的概率分类器链对其分类并组合所有分类结果.这样在充分考虑标记间依赖关系的同时,又有效地降低了概率分类器链的时间复杂度.
给定标记子集大小k,划分大小为m的初始标记集合L的最简单策略就是将其划分为n=「m/k⎤个互不相交的子集l1,l2,…,ln,其中从l1到ln-1,各子集的大小都为k.如果m为k的整数倍,则子集ln的大小也为k,否则其大小为m除以k的余数,即包含L中最后小于k个标记.此时,将各标记子集看作一个单独的分类任务,分为针对其学习一个分类器.
划分标记子集后的下一关键步骤是为每个标记子集li生成其相对应的训练实例集合Di.此处采用了与基于二值的BR转化类似的方法,Di包含了原始实例集合D中的所有实例.对训练集D={(x1,C1), (x2,C2) ,…, (xn,Cn)}中的实例xi,首先设其有|li|个标记,|li|为标记子集li中包含标记的个数.然后针对li中的每一个标记lij,若lij∈Ci,则将实例xi相对应标记设为1,否则就设为0.可见,该转化过程与BR转化类似,不同的是BR转化只针对一个标记,而此处是针对多个标记.生成训练集后,即可为每个标记子集训练一个概率分类器链.因此,基于该划分策略的算法流程如算法1所示.
算法1 RAKPCC算法的训练过程
输入:训练集合D={(x1,C1),…,(xn,Cn)},标记集L,标记子集大小k.
输出:随机划分的n=「m/k⎤个标记子集,以及在其上训练的概率分类器链.
算法流程:
01.将原标记集L划分成n=「m/k⎤个不相交的标记子集,并生成其相应的实例集合Di;
02.设i等于1,循环加1,直到i等于n.在第i次循环过程中为第i个标记子集li训练一个分类器链.循环过程为:
对标记子集li中的标记进行排序,
设j等于1,循环加1,直到i等于j=|li|,循环过程为:
(1)设Dij={},
(2)对Di中的每个实例d=(x,C),产生一个新属性集合x′={x,λ1,λ2,…,λi-1},生成新实例d′=(x′,λi)并将其添加到Dij中,
(3)在实例集合Di训练针对第i个标记的一个二类分类器:
fi:Dij→{0,1},
(4)生成分类器链CCi=(f1,f2, …,f|li|);
03.返回n个分类器链(CC1,CC2,…,CCn).
当对待测实例x分类时使用所有的概率分类器链,每个分类器链只针对其所对应的标记子集进行,然后组合所有分类器链的分类结果即可得到最终的分类结果向量.分类过程如算法2所示.
算法2 RAKPCC的分类过程
输入: 待测实例x.
输出: 实例x的标记向量Y=(y1,y2,…,yn),其中yk=1表示x属于第k个类,yk=0表示x不属于第k个标记.
算法流程:
01. 设标记向量Y为空,Y← {};
02. 设i等于1,循环加1,直到i等于n.在第i次循环过程中使用第i个概率分类器链对x进行分类. 找出联合概率最大的标记向量值yi;
03. 组合各分类器的结果向量返回分类结果Y=(y1,y2,…,yn).
所提出的算法相比基本的概率分类器链极大地简化了概率分类器链算法的计算效率.概率分类器链的时间复杂度为O(2m),RAKPCC的时间复杂度仅为n*O(2k),n=「m/k⎤为标记子集个数.例如,当标记集L的大小m为20时,为遍历每种可能的分类结果,概率分类器链需要训练220-1=4095个分类器,而将L划分成k= 5的子集时,仅需训练4*(25-1)=124个分类器,当k取更小时,所需训练的分类器更少.
2.3 基于随机标记子集的多标记数据流分类算法
本文提出的采用基于随机标记子集的多标记数据流分类算法(Multi-Label ensemble with Adaptive Windowing,MLAW),采用RAKPCC在不同时间段的数据块上学习,顺序产生组合分类器.当一个新的数据块达到时,根据其在当前最新数据块上的评价更新它们的组合权重,采用最大投票策略预测待分类实例的类别.
同时,在集成算法中引入了自适应滑动窗口算法[21](ADaptive WINdowing, ADWIN)来处理概念漂移.其核心思想是:把W划分为两个子窗W0和W1,监测这两个子窗口中数据分布的变化.当两个子窗口均值大于εcut,则表示两子窗口的期望值不一致,进而认为两个子窗口之间概念不相同,即发生概念漂移.εcut根据Hoeffding Bound不等式获得:
(1)
其中:δ(0, 1)为置信度,|W0|和|W1|分别表示W0和W1长度,且满足W= |W0|+|W1|.
用E= {C1,C2, …,Ck}来表示由k个组合分类器组成的集成,C′表示建立的新分类器.采用滑动窗口模型把数据流划分成大小相等的数据块,对于源源不断到达的实例(xi,yi),用ADWIN检测概念漂移,当检测到有概念漂移发生,则新建一个分类器加入到分类器池中,替换性能最差的分类器.接着根据每个基分类器Ci(i= 1, 2, …,k)在最新数据块上的分类情况,按公式(2)对采用非线性的方式对其进行加权.
(2)
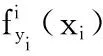
算法3 本文算法伪代码
输入:数据流S, 自适应滑动窗口检测器D, 分类器数k, 数据块大小d;
输出: 集成分类器E;
01:for 所有xt∈Sdo;
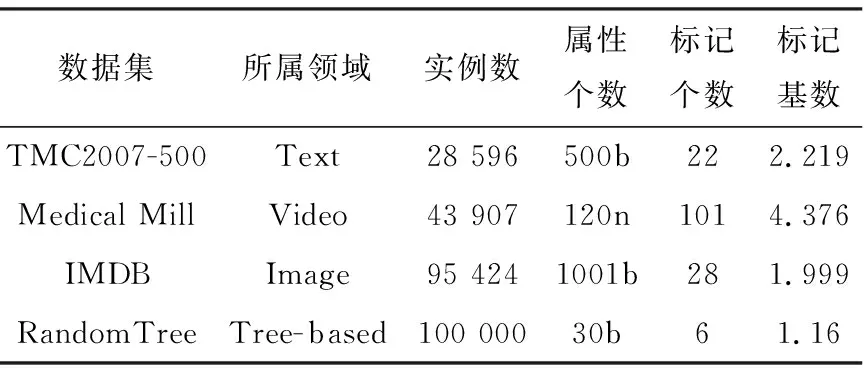
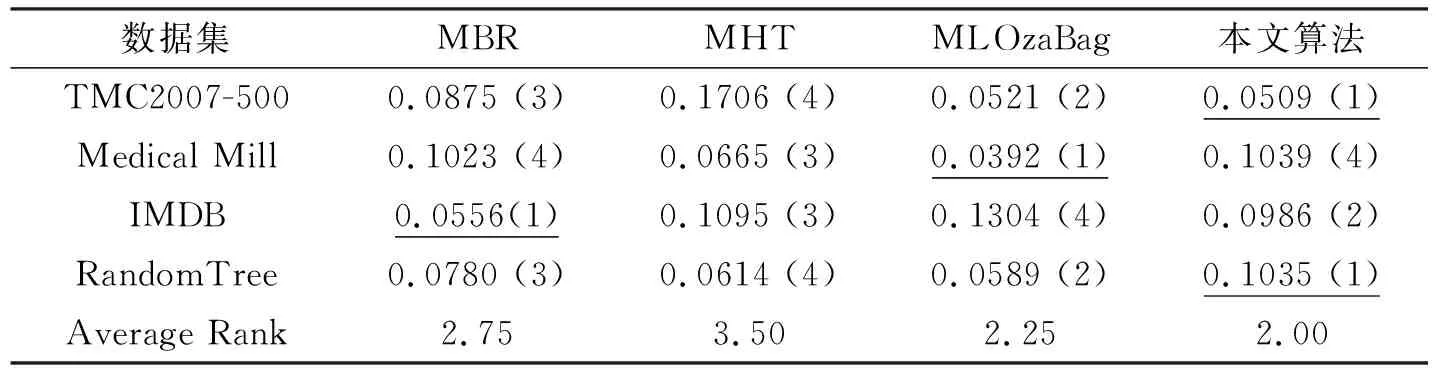
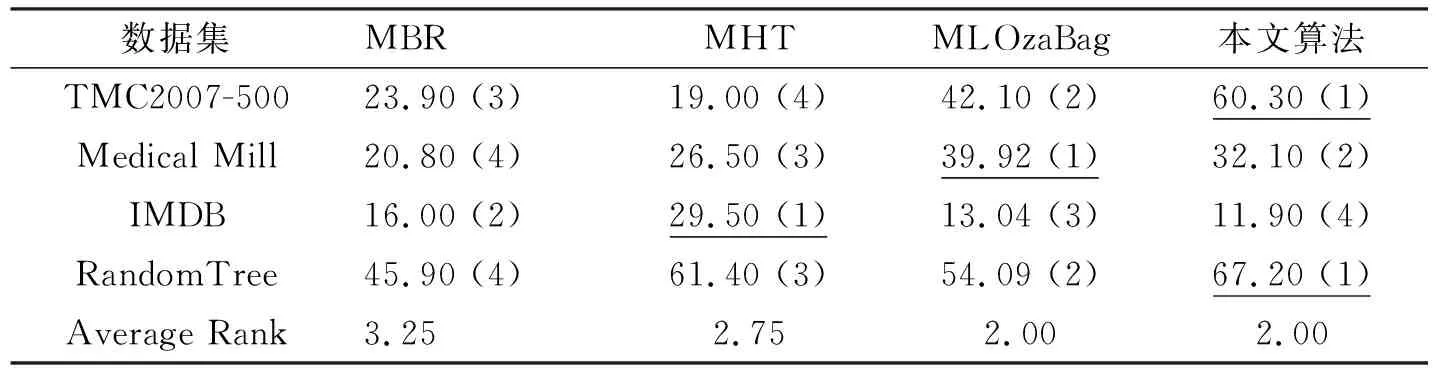
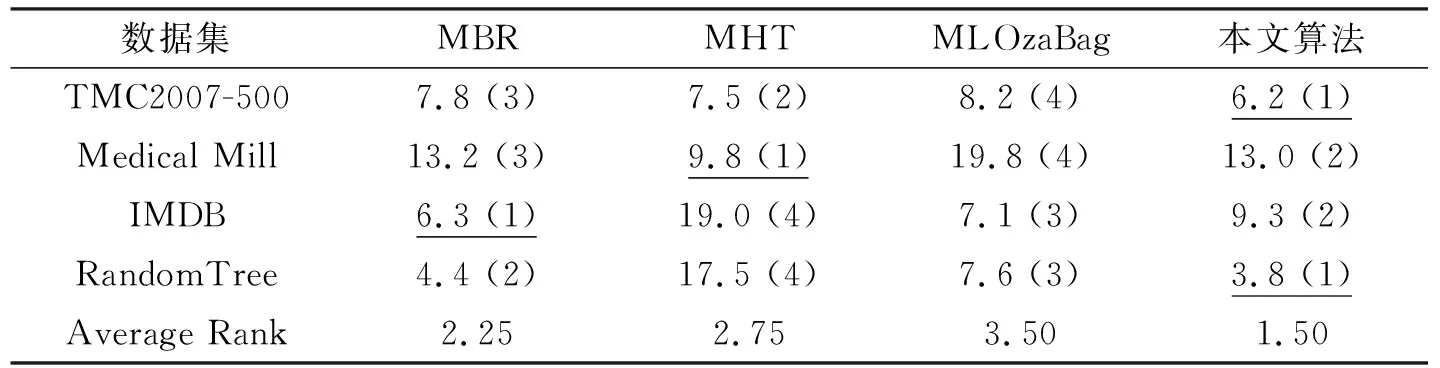
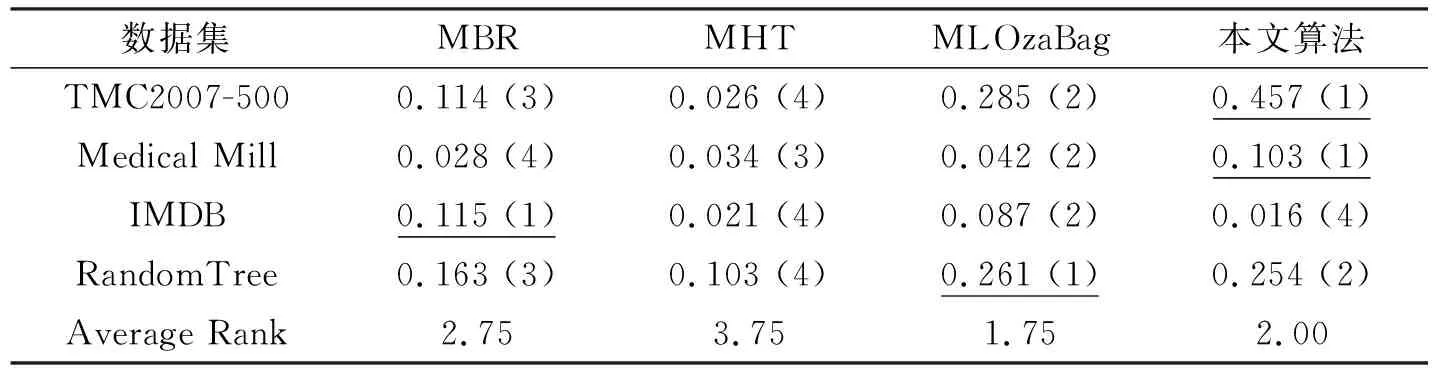
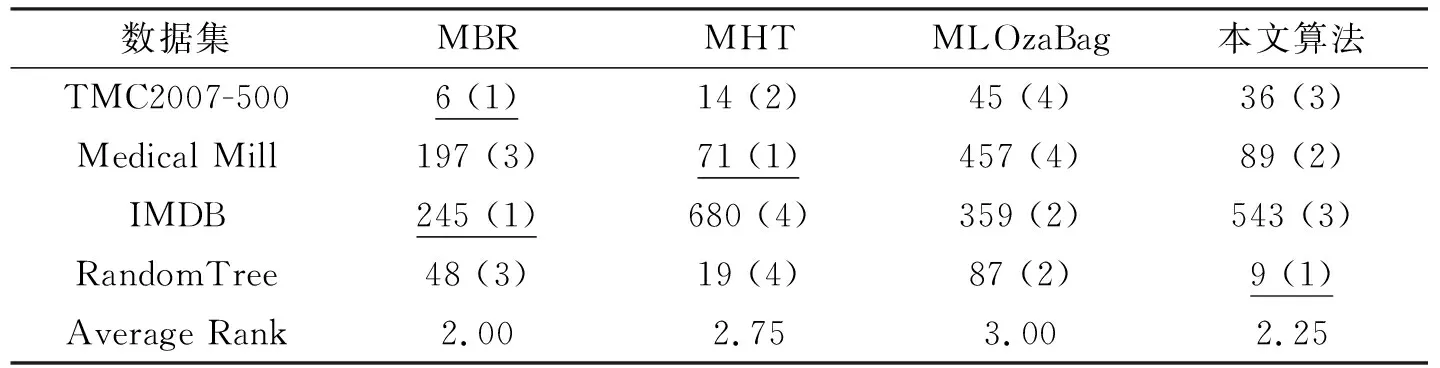
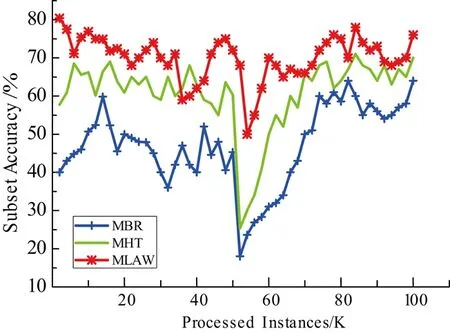
02: if |W| 03: else 用xt替换窗口中最早的实例; 04: 对所有基分类根据公式(2)加权; 05: iftmodd== 0 or 检测到有概念漂移发生 then; 06: 用RAKPCC算法在最新的数据块上建立新的分类器C′; 07: if |E| 08: else 用C′替换集成分类器中性能最差的分类器; 09: end if 10: end if 11:end for. 本文实验分别选取4数据集对所提出模型进行验证,如表1所示. 表1 数据集合基本信息Tab. 1 The characteristics of datasets 实验是在MOA(Massive Online Analysis)下实现的,所提算法与MBR, MHT和MLOzaBag以下算法进行对比:算法使用MOA平台下的默认参数.对于集成算法:数据块大小设置为1000,基分类器数目为15.自适滑动窗口概念检测算法的参数:置信度δ=0.002.分别从海明损失、子集准确率、F1测度、召回率和运行时间共5个方面性能进行比较. 从表2~表5中可以看出,本文所提出算法在总体上优于其他3种算法,特别是在汉明损失、子集正确率和召回率3个项指标上,优势较为明显. 表2 不同算法的汉明损失Tab. 2 Hamming loss of different algorithms 表3 不同算法的子集准确率(%)Tab. 3 Subset Accuracy of different algorithms 表4 不同算法的召回率Tab. 4 Recall of different algorithms 表5 不同算法的F1值Tab. 5 F1of different algorithms 这是由于本文算法具有概念漂移检测机制,因此能较好适应于概念漂移的数据流环境.在运行时间方面,如表6所示,单分类器MBR算法消耗时间最少,其次是本文算法,MLOzaBag算法消耗时间最长.这样由于本文基于随机划分的标记子集的概率分类器链算法,在充分利用标记间依赖关系的同时,又有效地降低了概率分类器链的时间复杂度,因此在时间上要有优势.单分类器算法MBR虽然速度最快,但却在分类准确率上表现最差. 图1给出了算法在概念漂移的环境下分类准确率随着处理数据增多而变化的情况.通过分析发现,当在50 K处发生概念突变时所有算法的准确率曲线均出现不同程度的下降,而本文算法的准确率曲线相对平稳,受到数据中概念漂移影响最小.这正验证了本文自适应滑动窗口的概念漂移检测方法,能够指导分类模型进行及时更新,从而适应概念漂移的环境.而MHT和MBR波动较大,这时由于这两个算法在设计中并未考虑概念漂移的问题,因此不适合不平稳的数据流环境. 表6 不同算法的消耗时间 (s)Tab. 6 Running time of different algorithms 图1 Random Tree数据集上分类准确率比较Fig. 1 Accuracy on the Random Tree dataset 本文针对多标记数据流中概念漂移现象,在考虑标记间依赖关系的基础上,设计并实现一种具有更好适应性的基于随机标记子集的多标记数据流分类算法.算法采用自适应滑动窗口算法作为一个概念漂移检测器引入到数据流集成算法中,通过在人工合成和真实数据集上进行比较发现,所提模型能够应对概念漂移,该算法在大多数数据集合上能够更有效地预测实例的类标集合.3 实验评价
3.1 数据集描述
3.2 实验结果分析
4 结束语
