V2G模式下基于电动汽车分群方法的配电网多目标优化运行策略
2018-08-08梅哲詹红霞苑吉河黄虎张曦邓强
梅哲, 詹红霞, 苑吉河, 黄虎, 张曦, 邓强
(1.西华大学电气与电子信息学院, 成都市 610039;2.国网重庆电力公司南岸供电分公司, 重庆市 400060)
0 引 言
当今能源问题,让人们逐渐意识到传统燃油汽车对环境以及可持续发展战略的负面影响。最近几年,发展和使用电动汽车成为一种趋势。虽然电动汽车能带来很多益处,但大量文献研究表明,电动汽车的无序入网会给电网的安全稳定运行带来挑战,比如进一步增大负荷峰值[1]、增大网损和影响电能质量[2]、减少变压器的寿命[3]等。因此,为了合理地使用电动汽车,对其进行有序充放电的引导十分有必要,V2G(vehicle to grid)模式则是良好的实现途径与解决办法。所谓V2G指的是,在电网负荷低谷利用电动汽车充电,而在负荷高峰时利用其向电网反馈电能,能够有效地削峰填谷与优化间歇性能源入网[4]。
针对电动汽车无序入网所带来的不良影响,国内外研究人员和学者做了大量研究。文献[5]以充电费用最低和电网的负荷方差最小为目标,提出了一种电动汽车智能充电调度策略,但是只将电动汽车当作用电负荷来优化,并未考虑其放电策略。文献[6]考虑到电动汽车用户的支持是实现V2G的基础,建立了包含电动汽车用户成本的多目标优化模型,所得结果也更符合实际情况,但并未考虑用户充电满意度与电网负荷方差。文献[7]提出了两阶段优化的电动汽车充电策略,以总成本最低为目标并且考虑了可再生能源的不确定性,但并未考虑放电的情况。
对于引导电动汽车有序充放电,有群体调度与个体调度2种策略。个体调度适用于电动汽车数量较少的情况,文献[8]搭建了对每辆电动汽车进行充放电优化的实时调度模型,但随着入网车辆增多,会使得变量维度过于庞大,求解困难甚至无解。文献[9]构建了电动汽车集群模型,并用于电力市场分析中。文献[10]提出了一种动态分群策略,求解速度较快且经济性也有所改善。文献[11]为了对电动汽车进行调度,利用遗传算法搭建随机参数的电动汽车集群模型。群体调度虽然大大减少了算法维度,但不能完全考虑到单辆汽车的电量、充电时间等特性参数,所以并不能很好满足车主的出行需求,理论性强,难以适用于实际情况。文献[12]提出了考虑了用户满意度的分群策略,但对于电动汽车的优化只考虑了时间维度,空间维度并未考虑。
本文在上述研究的基础上,为了减小电动汽车无序入网与分布式能源的波动性给电网带来的影响,提出一种V2G模式下基于电动汽车分群方法的配电网多目标优化运行策略。该策略对源网荷(分布式能源、配电网、电动汽车负荷)三方进行协调优化,基于电动汽车充放电与分布式能源配合,得到配电网的最优运行工况。该策略也提出了一种电动汽车分群方法,在减少变量维度的同时保障了车主的出行需求。
1 配电网多目标优化运行模型
电动汽车负荷与分布式能源接入配电网后,为了使源网荷三者协调互动起来,本文提出的优化运行模型有3个目标函数:电动汽车车主费用最低、配电网负荷均方差最小以及配电网网损最小。由于源网荷三者的关系是“供销用”,因此三者在收益层面不可能同时为最优,但却可以“各取所需”。车主利用分时电价政策少花钱,则电网的收益会降低,但是却换来负荷的平稳及电网的安全运行,通过对电动汽车合理充放电管理可消纳更多的分布式能源,从而增加源侧收益。当然这都是基于电动汽车与电网的良性互动,因此首先要保证车主的利益;配电网的平稳运行是最终要求,则网侧的负荷波动与网损要小;在保证网荷利益的基础上,源侧利用分布式能源与电动汽车充放电配合,使配电网处在一个最优运行状态。该模型有多个目标、多个约束,前2个目标是系统宏观层面上的,与网络结构关系不大;而网损则涉及到配电网拓扑结构,因此为了更好地对模型求解,将模型拆解为内外嵌套模型。内层模型的目标是电动汽车车主费用最低、配电网负荷均方差最小,外层模型目标则为配电网网损最小。
1.1 模型搭建
上述内外嵌套模型,内层模型优化所得结果会作为初值反映在外层模型中,外层模型得出的结果也会反馈在内层模型中,进行下一次的迭代。这样反复迭代,当满足终止条件时,优化迭代就结束,输出最优结果。内外嵌套模型的求解流程如图1所示。
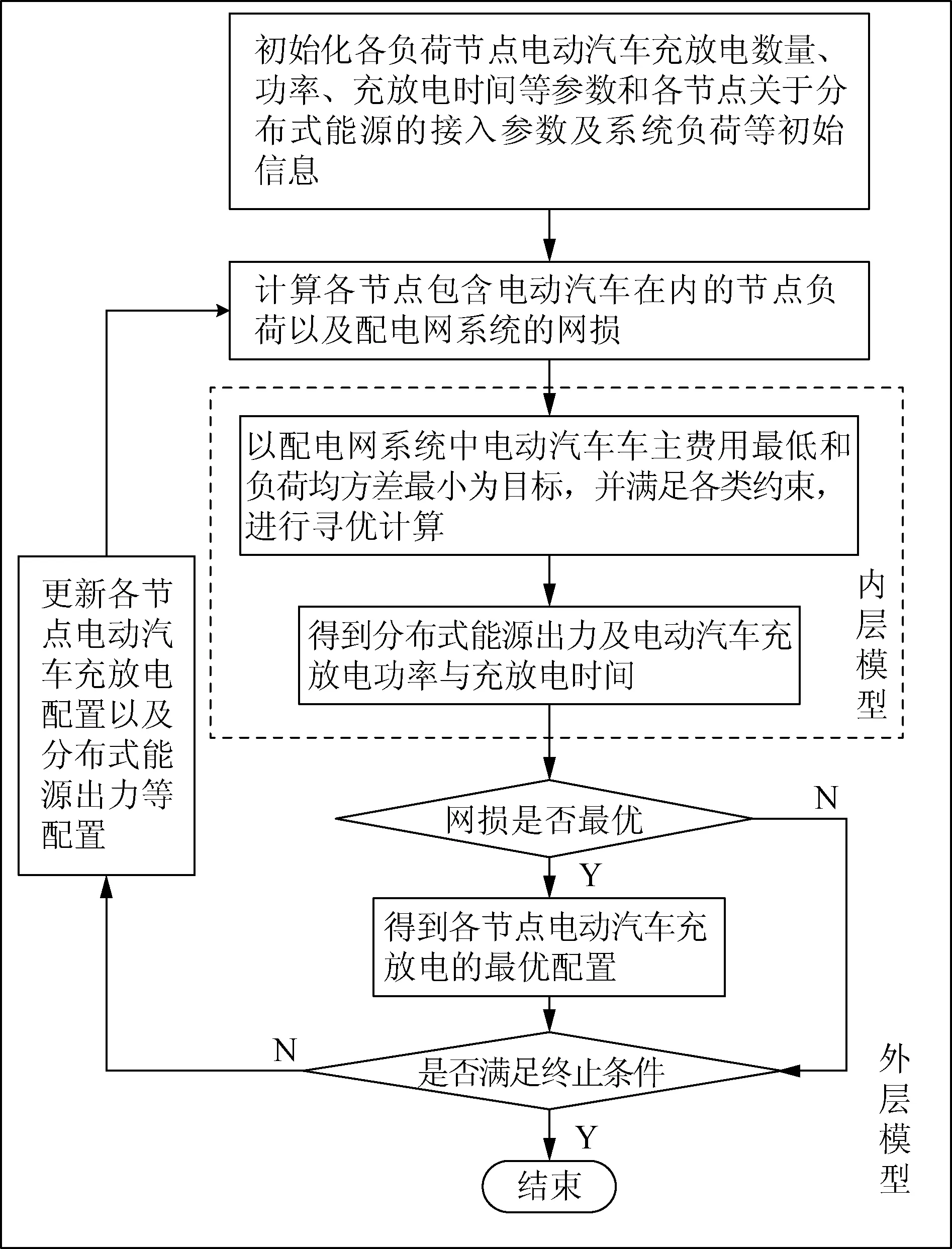
图1 内外嵌套模型求解流程图Fig.1 Flowchart to solve internal and external nested model
内外层模型的目标均是最优化问题,因此采用GA-PSO(genetic and particle swarm optimization algorithm)混合优化算法对该模型求解。该算法既有PSO算法的快速寻优能力,又有GA算法能跳出局部最优陷阱的能力,很好解决了单一算法的局限性。
1.2 内层模型
1.2.1目标函数
(1)电动汽车车主费用最低。车主费用的高低决定着电动汽车参与程度,因此要保证车主的利益。
λEV[PEVD(i,t)μEVD(i,t)+PEVC(i,t)μEVC(i,t)]-
CEVD(i,t)PEVD(i,t)μEVD(i,t)}ΔT
(1)
式中:FEV表示车主费用,考虑车主充电费用、充放电对电池寿命造成的损失以及向配电网放电所得收益,其值为前两者之和减去后者;T表示优化周期;ΔT为优化步长;NEV表示电动汽车数量;CEVC(i,t)表示t时段电动汽车i的单位充电电价;PEVC(i,t)表示t时段电动汽车i的充电功率;μEVC(i,t)表示t时段电动汽车i的充电状态,为0或1;同理,CEVD(i,t)表示t时段电动汽车i的单位放电电价;PEVD(i,t)表示t时段电动汽车i的放电功率;μEVD(i,t)表示t时段电动汽车i的放电状态;λEV表示电动汽车的电池老化系数。
(2)以配电网负荷均方差最小为目标。其表征电网的负荷波动情况,值越小则表示负荷变化越平稳。
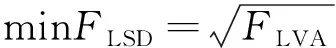
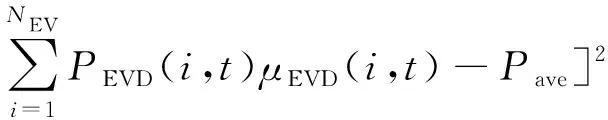
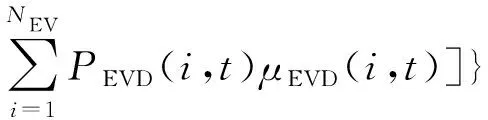
式中:FLSD表示配电网的负荷均方差;FLVA表示配电网负荷方差;Pload(t)表示t时段配电网原有负荷大小;PDG(i,t)为t时段分布式能源机组i的出力;NDG为分布式能源机组数量;Pave表示配电网原有负荷、分布式能源机组出力和电动汽车充放电功率的平均值。
1.2.2约束条件
(1)系统有功平衡约束。
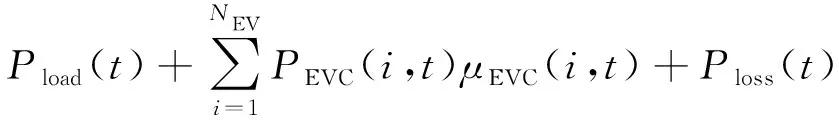
式中:Pg(t)为t时段上级电网向配电网注入有功功率;Ploss(t)为t时段配电网网损大小。
(2)峰谷差约束。优化之后的负荷峰谷差要小于原始负荷的峰谷差。
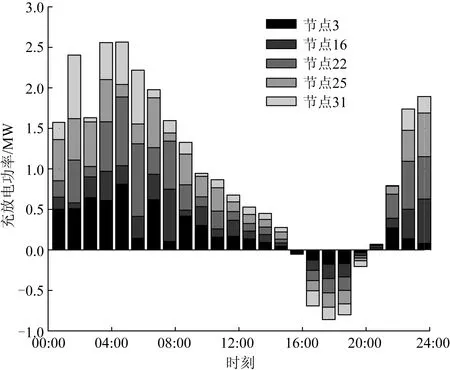
Pload,max-Pload,min (6) 式中:Pload0,max、Pload0,min分别表示配电网原负荷峰值、谷值;Pload,max、Pload,min分别表示优化之后的负荷峰值、谷值。 (3)本文考虑的分布式能源有小水电,其约束条件不同于风光等新能源。式(7)表示水电机组水电转换关系约束,式(8)为水电机组出力上下限约束,式(9)表示水电机组发电引用流量上下限约束,式(10)为水库库容量约束,式(11)表示水量平衡约束。 PHP(i,t)=KHP(i)qi,tHi,t (7) PHP(i,min)≤PHP(i,t)≤PHP(i,max) (8) qi,min≤qi,t≤qi,max (9) Vk,tmin≤Vk,t≤Vk,tmax (10) Vk,t+1=Vk,t+(Ik,t-qk,t-dk,t)ΔT (11) 式中:PHP(i,t)为t时段水电机组i的出力;KHP(i)表示水电机组i所在水电厂的发电出力系数;qi,t为t时段水电机组i的发电引用量;Hi,t表示t时段水电机组i的水头,为上下游的水位差;PHP(i,max)、PHP(i,min)表示水电机组i的出力上下限;qi,max、qi,min表示水电机组i的发电引用流量上下限;Vk,t表示t时段水电厂k的库容量;Vk,tmax、Vk,tmin表示t时段水电厂k库容量上下限;Ik,t表示t时段第k级水电站的入库径流量;qk,t为t时段水电厂k的总发电引用流量;dk,t表示t时段水电厂k的弃水量。 1.3.1目标函数 该层的目标是配电网的总有功网损最小。 式中Floss表示优化周期内的配电网总网损。 1.3.2约束条件 外层模型的目标是网损最优,与分布式能源和电动汽车的接入位置及容量有关系,因此约束有潮流约束、电压约束和电动汽车约束。本文提出的充放电策略实质上是一种延迟优化策略,电动汽车出行结束开始接入充电桩充电时,该优化策略会依据此时配电网的负荷情况,同时对车辆的开始充电时刻与电量情况进行判断,决定车辆是充电还是放电,并计算出最优的电动汽车充放电时间与功率。 (1)多时段潮流平衡约束。 (13) (14) 式中:Pm,t、Qm,t分别表示t时段节点m的有功、无功注入;Nno表示系统节点总数;Um,t、Un,t分别表示t时段节点m、n的电压幅值;Gmn、Bmn分别为节点m、n之间的电导和电纳;θmn表示节点m与n之间的电压相角差。 (2)节点电压约束。 Um,min≤Um,t≤Um,max (15) 式中Um,max、Um,min为节点m的点电压幅值上下限。 (3)电动汽车充放电功率约束。 PEVC,min≤PEVC(i,t)≤PEVC,max (16) PEVD,min≤PEVD(i,t)≤PEVD,max (17) 式中:PEVC,max、PEVC,min表示电动汽车充电功率的上下限;PEVD,max、PEVD,min表示电动汽车放电功率的上下限。 (4)电动汽车电池容量约束。 SSOC(i,min)≤SSOC(i,t)≤SSOC(i,max) (18) 式中:SSOC(i,t)为t时段电动汽车i的电池荷电状态(state of charge,SOC);SSOC(i,max)、SSOC(i,min)表示电动汽车i的SOC上下限。 (5)电动汽车车主期望电量约束。 SSOC,departure(i)≥SSOC,expect(i) (19) 式中:SSOC,departure(i)为电动汽车i离开时的SOC水平;SSOC,expect(i)为电动汽车i车主希望达到的SOC水平。 (6)电动汽车电量平衡约束。 SSOC(i,t+1)=SSOC(i,t)+[μEVC(i,t)× PEVC(i,t)-μEVD(i,t)PEVD(i,t)]ΔT/EEV(i) (20) 式中EEV(i)表示车辆i的电池容量。 (7)充放电时间约束。对于电动汽车的充放电优化策略是在不影响车主正常出行的条件下进行的,假设车主每天08:00出门上班,那么在08:00前车辆的电量必须要达到车主的要求。式(21)表示电动汽车最大充放电延迟时间约束;式(22)为放电电量约束,为了延长电池使用寿命,不能对电动汽车进行过放[13];式(23)为充放电时间约束[12]。 (22) Td,i+TdEVD,i+TEVD,i+TdEVC,i+TAEVC,i≤Tdmax.i (23) 式中:Tdmax,i表示电动汽车i的最大充放电延迟时间;TCX,i为用户i出行时刻,本文假设的是每天08:00;TKC,i表示电动汽车i开始充电时刻,即出行结束接入充电桩时刻;TEVC,i为达到用户期望电量所需的充电时间;TEVD,KC表示放电开始时刻;TEVD,END表示放电结束时刻;ΔtEVD为放电周期间隔;α为最低放电系数,一般取20%;Td,i表示车辆i的充电延迟时间;TdEVD,i与TEVD,i分别表示车辆i的放电延迟时间与放电时间;TdEVC,i表示放电结束再充电延迟时间;TAEVC,i为再次充电达到用户电量需求持续时间。 (8)电动汽车充放电状态约束,同一辆电动汽车不能同时充放电。 μEVC(i,t)+μEVD(i,t)≤1 (24) 由于电动汽车数量众多,每辆车的开始充电时刻、充放电时间等车辆特征信息都不尽相同,如果一一对每辆车充放电优化,这就意味着待优化的变量众多,导致算法维度过大,使得求解困难甚至无解。为此,本文提出了一种对电动汽车分群的方法,该方法在符合实际情况易于求解的同时,也考虑了车主的出行需求。 本文提出的方法是对于周期为24 h的优化分群,可将同一时间段内开始充电的电动汽车分为同一类群,比如在同一小时内的分为一类;在同一时段内的汽车所需充电时间亦不一样,将充电时间接近的汽车分为一类。据统计数据,大部分电动汽车的充电时间都在3 h内,因此可将其再进行分类,如把充电至车主期望电量所需时间在1 h内的分为一类,1~3 h的分为一类,大于3 h的分为一类。因此就有了电动汽车分群特征值TKC和TEVC,这里TKC表示电动汽车的开始充电时刻,TEVC表示充电至车主期望电量所需时间。 将电动汽车分群处理后,每个子群的车辆何时该放电,何时该充电呢?而且为了保护电动汽车电池寿命,不能随意地对其一天内进行多次充放电。为此,本文提出了一种基于分群方法的充放电策略,将充放电形式分为2种,一是充电-放电-充电,二是放电-充电-充电。 (1)充放电形式一:充电-放电-充电,其充放电示意图如图2所示。 TCDC,I=TKC+Td+TFEVC (25) TCDC,II=TCDC,I+TdEVD+TEVD (26) TCDC,III=TCDC,II+TdEVC+TEVC (27) 式中:TCDC,I表示充放电形式一的第I阶段结束时刻;TCDC,II表示充放电形式一的第II阶段结束时刻;TCDC,III表示充放电形式一的第III阶段结束时刻;TKC为电动汽车的开始充电时刻,指的是电动汽车接入充电桩的物理开始时刻,仅表示此刻车主将电动汽车接入充电桩,而真正与电网交换电能的时刻还与其余优化变量有关系;Td表示开始充电时对应的充电延迟时间;TFEVC表示刚接入时到充满所需时间;TdEVD为放电延迟时间;TEVD为放电时间;TdEVC为再次充电延迟时间;TEVC表示充电至车主期望电量所需时间。 图2 充放电形式一示意图Fig.2 Diagram of charging and discharging Form 1 结合图2对公式(25)—(27)进行说明。式(25)为电动汽车接入到电量充满阶段,对应图2中阶段I;式(26)为从充满到放电阶段,对应图2中阶段II;式(27)为放电结束到充电至车主期望电量阶段,对应图2中阶段III。充放电形式一适用于电动汽车刚接入时电量不充足的情况,对应子群内所需充电时间较长的电动汽车。 (2)充放电形式二:放电-充电-充电,其充放电示意图如图3所示。 TDCC,I=TKC+TdEVD+TEVD (28) (29) TDCC,III=TDCC,II+Td+TEVC (30) 式中:TDCC,I表示充放电形式二的第I阶段结束时刻;TDCC,II表示充放电形式二的第II阶段结束时刻;TDCC,III表示充放电形式二的第III阶段结束时刻;PC与PD分别表示充放电功率,所在分式含义为求出充回放掉电量所需时间。 图3 充放电形式二示意图Fig.3 Diagram of charging and discharging Form 2 结合图3对公式(28)—(30)进行说明。式(28)为接入到放电阶段,对应图3中阶段I;式(29)为放电结束到充电至刚接入时刻电量的阶段,对应图3中阶段II;式(30)为继续充电至车主期望电量阶段,对应图3中阶段III。充放电形式二适用于对应子群内充电所需时间较短的电动汽车。 对于同一子群的电动汽车,执行相同的充放电策略,即有相同的充电延时、放电延时、放电时间及放电后再充电延时,而充电至车主期望所需电量时间仍按照每辆车的实际情况来决定,这样既大大减少了变量维度,又保障了车主出行需求。基于本文分群方法的充放电策略,使得电动汽车一天内不会多次随意充放电,保护了电池,延长了车辆使用寿命;也对数量众多的电动汽车进行分群优化,更符合实际情况且利于调度;同时也保证了车主的用车需求。 本文采用修改过的IEEE 33节点配电系统,来验证提出的V2G模式下基于电动汽车分群方法的配电网多目标优化运行模型与分群理论的有效性。本文提出的模型优化运行周期考虑为一天24 h,因此需要每1 h的负荷数据,依据各个节点有功功率占系统总有功功率比例不变的假设[14],将某区域电网典型日负荷折算到修改过的IEEE 33节点系统上。修改后的IEEE 33节点配电系统示意图如图4所示,图中EV、WT、HP分别代表电动汽车、风电与水电的接入。 图4 修改后的IEEE 33节点示意图Fig.4 Diagram of modified IEEE 33-bus distribution system 由于风、水2种资源具有很好的互补性[15],因此假设配电系统中分布式能源有风电与小水电,2台基准有功出力为400 kW的风机分别接在12和21号节点上。水电站由2台基准有功出力800 kW的水电机组构成,分别接在节点29与30上。其水位与库容的关系见表1,水电机组发电出力系数为7.5,单机最大发电引用流量为3.56 m/s。电动汽车充电点设在3,16,22,25,31这5个节点。负荷数据如图5中原负荷所示,典型日风电有功出力值如图6中风电所示。 表1水位与库容关系 电动汽车型号假设都为比亚迪e6,其参数来源于比亚迪官网,汽车电池容量82 kW·h,最大行驶距离400 km。相较于公用车,私家车可调度性更大,因此假设电动汽车类型都为私家车,用于上下班通勤,且本文数据都为工作日数据。为了简化模型,减少变量维度,认为充电功率恒定为7.8 kW,充电效率为0.9。由于V2G模式现在尚未普及,所以假设放电功率与充电功率相同。电池老化系数为0.13元/(kW·h)。电动汽车车主期望所需电量设置为95%。电动汽车充电分时电价如表2所示,同样假设放电电价与同时段充电电价相同。电动汽车出行结束时刻服从正态分布,均值为17.6,标准差为3.4,假设电动汽车出行结束时刻即开始充电时刻。电动汽车日行里程服从均值为3.7,标准差为0.9的对数正态分布[16]。 表2电动汽车充电分时电价 利用基于蒙特卡洛法的电动汽车充电负荷模型[17]先对2 000辆电动汽车无序充电进行仿真,得到每辆电动汽车的起始充电时刻、电池初始SOC,进而计算出充电至车主期望所需电量时间和电动汽车无序充电负荷。根据蒙特卡洛仿真得出的每辆电动汽车分群特征值,开始充电时刻TKC和充电至车主期望电量所需时间TEVC对这2 000辆汽车进行子群划分,分群原则与第2节中分群方法叙述举例一致。以子群为单位对本文所提优化模型求解,得到每一子群的充电延时、放电延时、放电时间及放电后再充电延时这4个特征控制量及小水电的优化出力。值得注意的是,每一子群内的每辆电动汽车充电时间仍是以每辆电动汽车各自的充电至车主期望所需电量时间为准,因此保障了车主的出行需求和充电满意度。 对于本文所提出的优化运行策略,在只有电动汽车无序接入(场景1)、分布式能源与电动汽车无序接入(场景2)、电动汽车有序充放电(场景3)和V2G模式下电动汽车与分布式能源配合(场景4)这4种场景下进行仿真。基于MATLAB平台采用GA-PSO混合算法对其进行求解,得到4种场景下的仿真结果对比,以验证本文所提出的优化策略的有效性。4种场景下配电网中各种有功功率曲线仿真计算结果如图5—8所示。 图5中电动汽车无序充电负荷高峰主要集中在17:00—24:00,这是由于车主从17:00开始陆续下班,驱车到家之后,立即就对电动汽车充电。在此后的几个时段内,充电负荷持续高峰,并且大部分电动汽车已在此高峰时段完成充电任务(完成充电后充电桩自动切断电源),因此夜间时段充电负荷较小。图5表明,电动汽车的无序接入会使得配电网负荷急剧增大,出现峰上加峰的情况。结合图6,可以看出分布式能源接入后,能起到改善负荷的作用,但此场景下电动汽车处于无序充电的情况,并未与分布式能源配合,因此对于负荷波动的平抑、峰谷差的控制都不尽如人意。对比图7与图5,可以发现引导电动汽车有序充放电能有效地降低负荷峰谷差、缓和负荷波动,但此场景下的负荷仍处于较高水平。 图5 电动汽车无序接入(场景1)时各有功功率曲线Fig.5 Active power curves with disordered charging of electric vehicles (Scenario 1) 图6 分布式能源与电动汽车无序接入(场景2)时各有功功率曲线Fig.6 Active power curves with distributed energy resource and disordered charging of electric vehicles (Scenario 2) 图8表明,V2G模式下电动汽车充放电与分布式能源相互配合,即电动汽车在负荷高峰时段与分布式能源一起向配电网供电,在负荷低谷时段充电消纳多余的分布式能源,此场景下,负荷水平相较与场景3有了约1/4的降低,负荷波动情况更是相较于场景1、场景2有了大幅改善。 图7 电动汽车有序充放电(场景3)时各有功功率曲线Fig.7 Active power curves with orderly charging and discharging electric vehicles (Scenario 3) 图8 电动汽车与分布式能源配合(场景4)时各有功功率曲线Fig.8 Active power curves with coordination of electric vehicles and distributed energy resource (Scenario 4) 值得注意的是,图8中电动汽车充电负荷从02:00到04:00有一个小幅波动,这主要是因为电动汽车充放电时间约束的限制,本文所提优化策略考虑的是08:00前要满足车主的充电需求。该策略实质上是一种延迟优化策略,具有负荷转移的作用,可将高峰充电负荷转移至凌晨负荷低谷时刻。 凌晨充电负荷慢慢变大,即从00:00开始负荷慢慢增加,这是整体充电负荷变化趋势,因此02:00时刻负荷增加;但由于电动汽车接入数量众多,每辆车的充电需求时间都不尽相同,有一些接入时刻较靠前且所需充电时间较短的电动汽车在03:00前已完成充电,所以在03:00时刻充电负荷又突然下降了一些;至于04:00充电负荷再次增加,也是本文所提优化延时策略的原因,虽然该策略具有负荷转移作用,但对于电动汽车充电负荷也是需要分配的,不然只是将17:00—24:00的充电负荷高峰转移至凌晨,变成凌晨负荷高峰、出现峰谷倒置的现象也是没有意义的。 基于此策略,高峰时段转移过来的电动汽车实际开始充电时刻也是不同的,使得在04:00有一些接入时刻靠后且所需充电时间较长的电动汽车开始充电,使得充电负荷增加。其次,电动汽车的充放电优化还要考虑与分布式能源出力配合,使配电网的负荷变化趋于平缓,本身分布式能源出力就有波动性,因此也造成了转移充电负荷在小范围的波动,有一定的随机性。但电动汽车充放电整体走势,依然是在配电网负荷高峰放电,在负荷低谷充电,与分布式能源配合,起到了削峰填谷的作用。 同时,也能得出这4种场景下网损与电压的对比。图9是24 h网损的变化,图10是18:00时4种场景下的电压水平情况。 图9 4种场景下的网损Fig.9 Power losses of network in four scenarios 图9表明,场景1、2的网损波动较大,场景3、4较平缓,且场景4网损水平最低。这是因为网损与负荷水平呈正相关的联系,场景1、2负荷波动大因而网损也波动大,场景4负荷水平最低因而网损也最低。从图10可以看出,场景1、2都出现了电压越限的情况,场景3、4则没有出现且场景4电压一直维持在较高水平,表明电动汽车合理的优化以及与分布式能源的配合,对于电压也能起到改善作用。 图10 18:00时4种场景下的电压Fig.10 Voltage at 18:00 in four scenarios 表3是4种场景下的车主费用、负荷均方差、网损、峰谷差与电压的数据对比。表3中,场景1与场景2的车主费用较高是因为电动汽车大量在负荷高峰时段充电,此时电价较高;场景3、4由于得到了合理的优化,在高峰放电、低谷充电,因而车主费用较低。4种场景下负荷均方差、网损、峰谷差与电压的数据变化也与上述分析一致,这里就不再赘述了。表3显示,场景4各项指标均是最优,为配电网提供了一种运行策略使其处在最优的状态,验证了本文提出优化策略的正确性。 表34种场景下结果对比 对于电动汽车的优化,基于本文提出的分群方法将电动汽车分为了63个子群,每个子群被优化得到相同控制策略,从而对该子群内的电动汽车进行具体充放电时间和地点的引导。表4是场景4优化后的各子群的特征控制量,由于子群数量太多,本文只列举其中10个子群的数据。 电动汽车的优化不仅存在着时间上的控制,为了使配电网网损最小,也存在着空间上的控制。图11是对电动汽车各接入点充放电功率的分配。图11显示,电动汽车在16:00—20:00之间向配电网反向供能,其余时刻则充电。 表4各电动汽车子群控制特征量 min 图11 电动汽车接入点功率分配Fig. 11 Power distribution at access points of electric vehicles 本文提出了一种V2G模式下基于电动汽车分群方法的配电网优化运行策略,对源网荷三方进行了协调优化。搭建了配电网多目标模型,考虑了车主利益,电动汽车与电网的良性互动因此得到了保障;考虑了配电网的负荷均方差和网损,使其峰谷差大幅减小、负荷变化趋于平缓,运行经济性也得到保障;分布式能源与电动汽车相互配合,使配电网处在一种最优运行状态。为更方便地对该模型求解,提出了一种电动汽车分群方法,基于电动汽车的开始充电时刻和车主期望电量充电所需时间2个特征值,得出了各电动汽车子群控制特征量与电动汽车充放电功率时空分配。4种场景下的算例分析表明,该策略在保障电动汽车车主利益的同时,可有效降低配电网负荷水平、平抑负荷波动、减小峰谷差、改善电压水平以及减小网损。1.3 外层模型
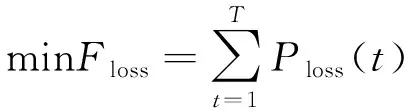
2 电动汽车分群方法
2.1 分群特征值
2.2 基于分群方法的电动汽车充放电策略


3 算例分析
3.1 算例数据
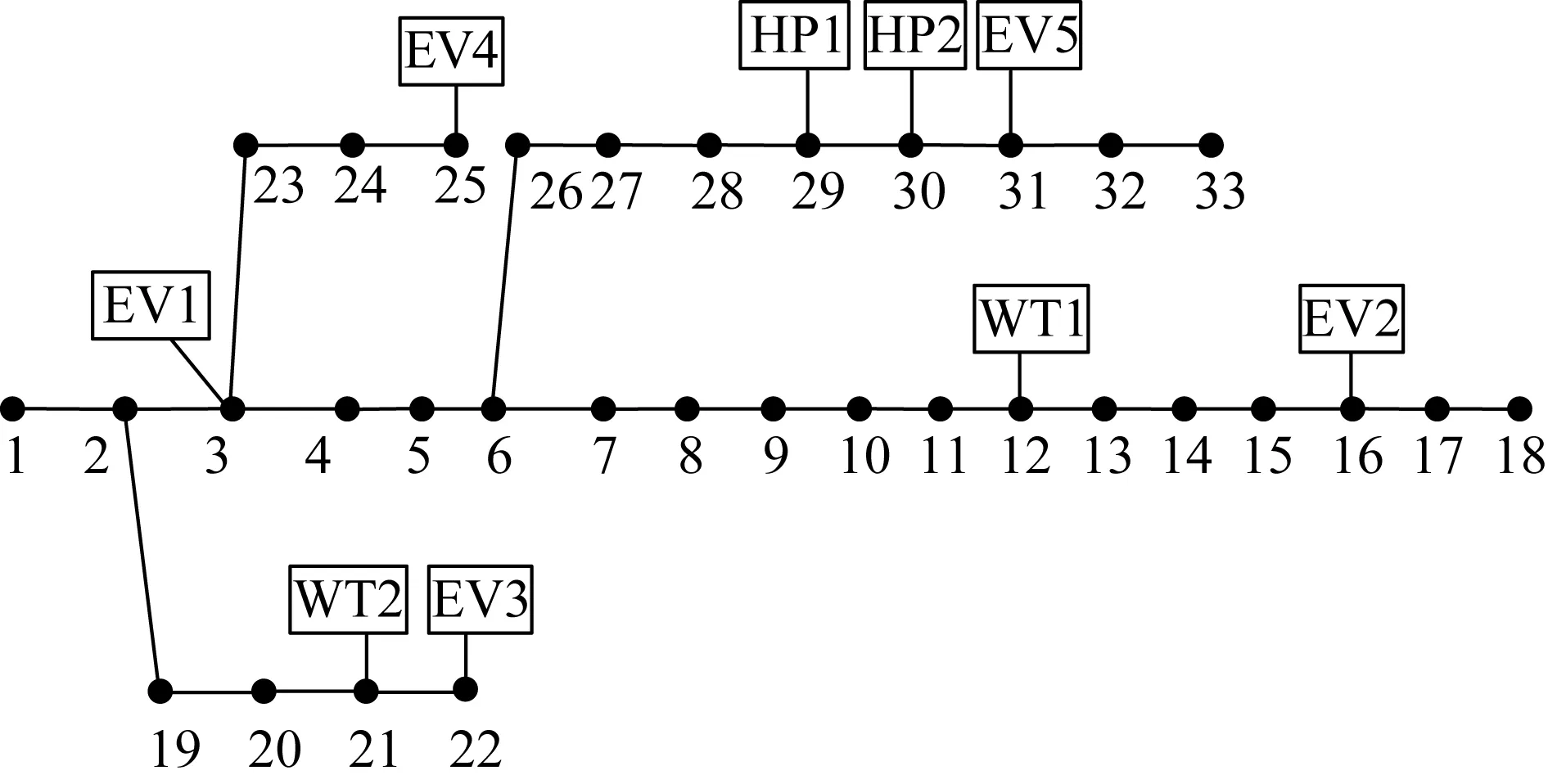
Table1Relationbetweenwaterlevelandcapacityofreservoir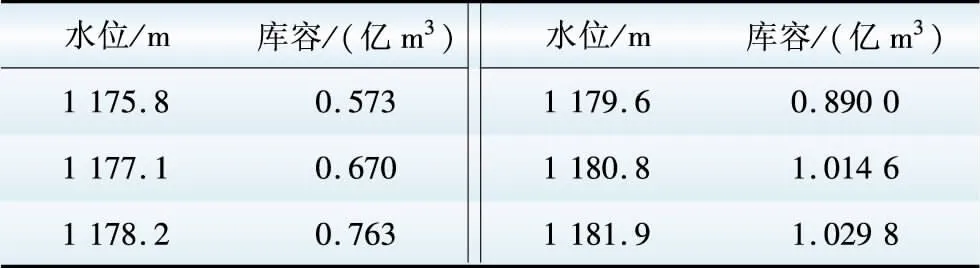
Table2Time-of-useelectricitypriceofelectricvehiclescharging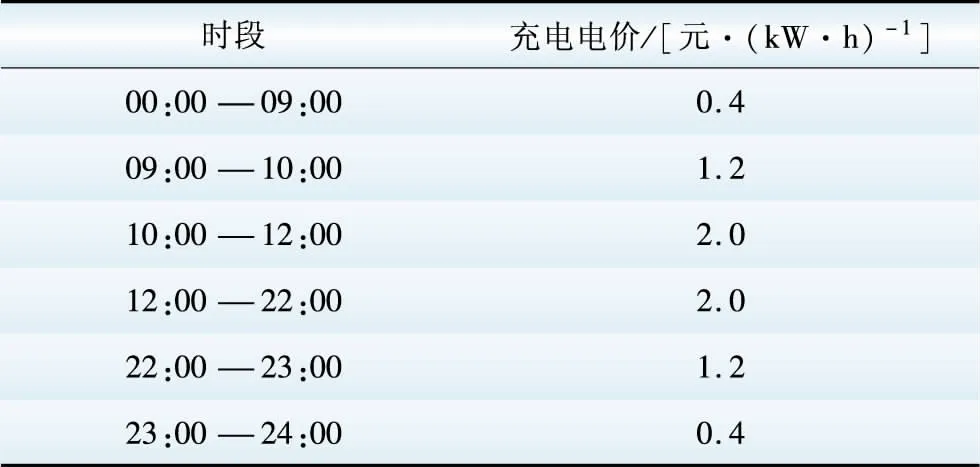
3.2 仿真结果与分析
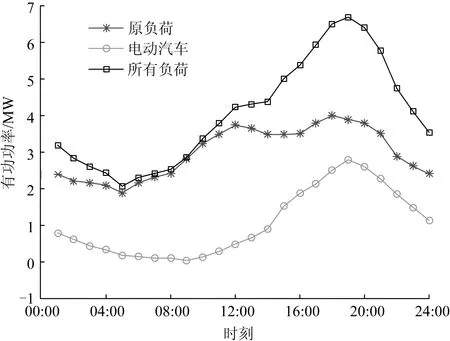
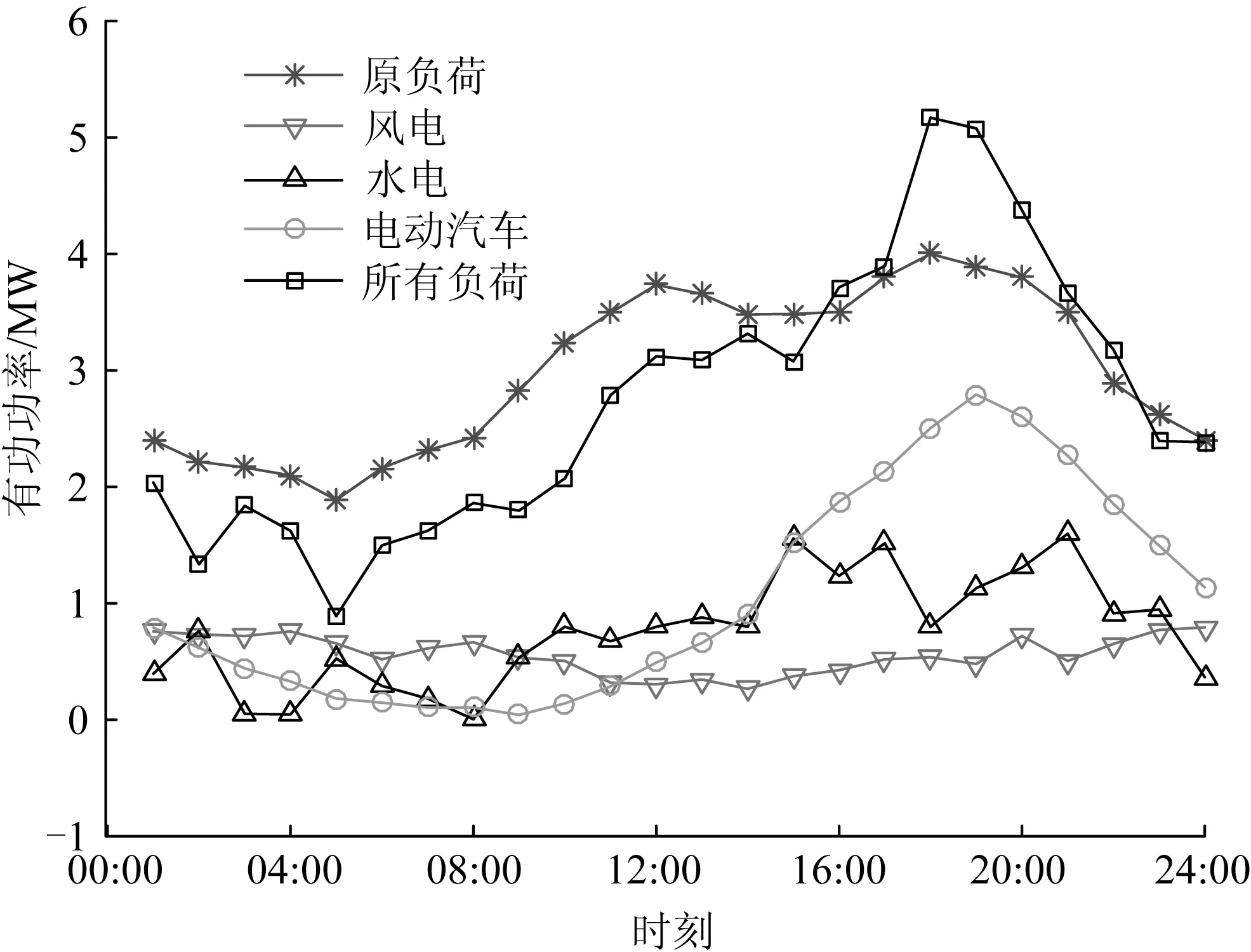
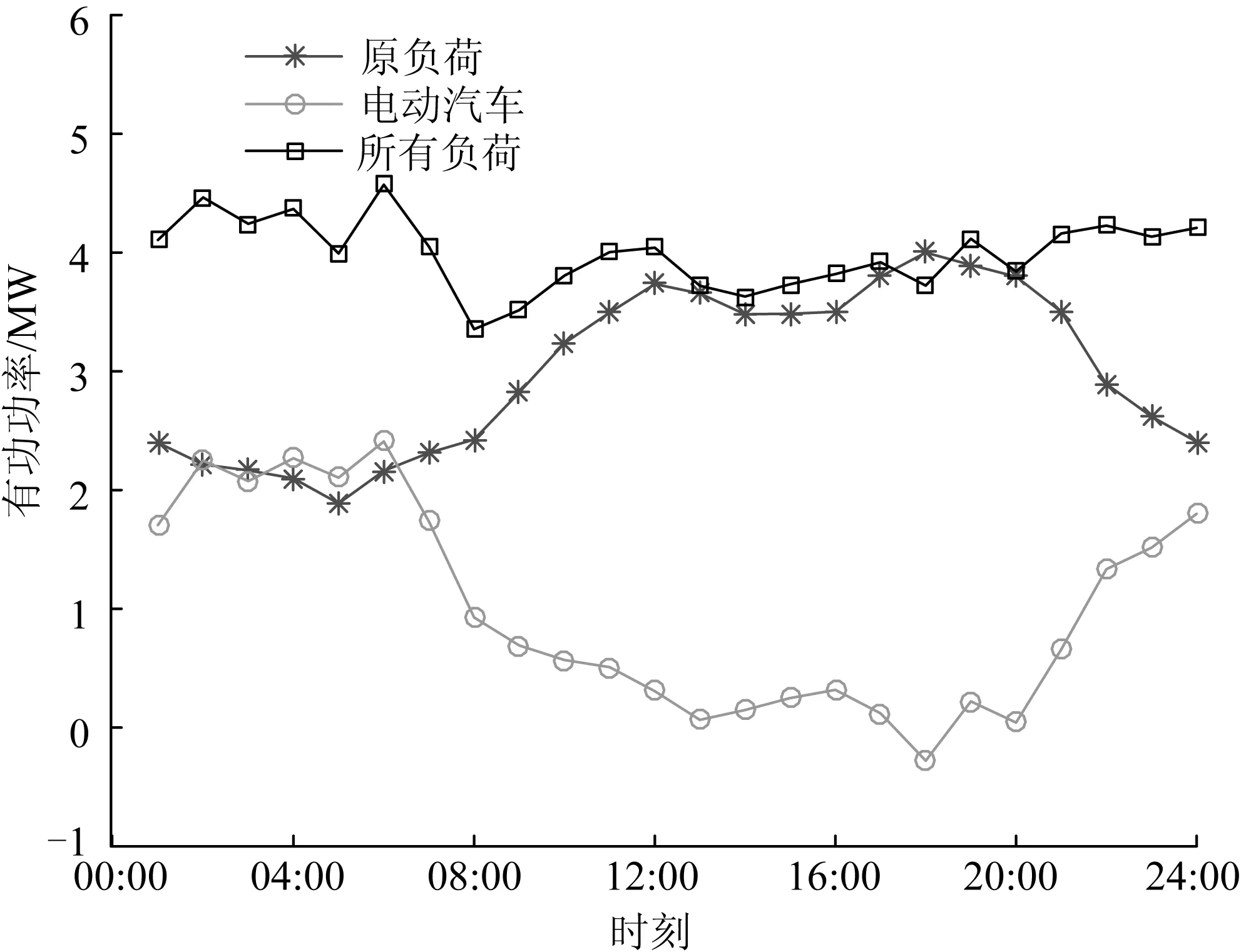
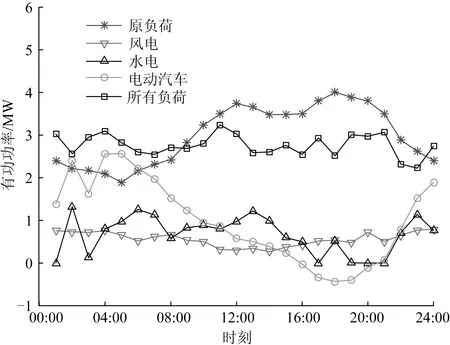
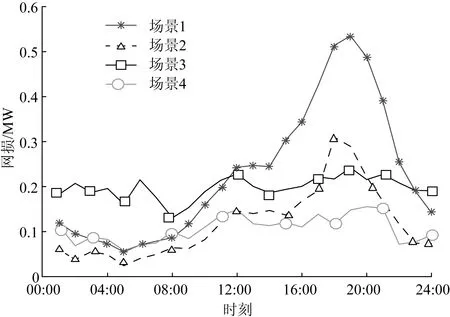
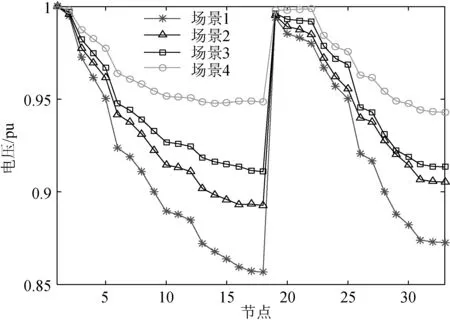
Table3Comparisonofresultsinfourscenarios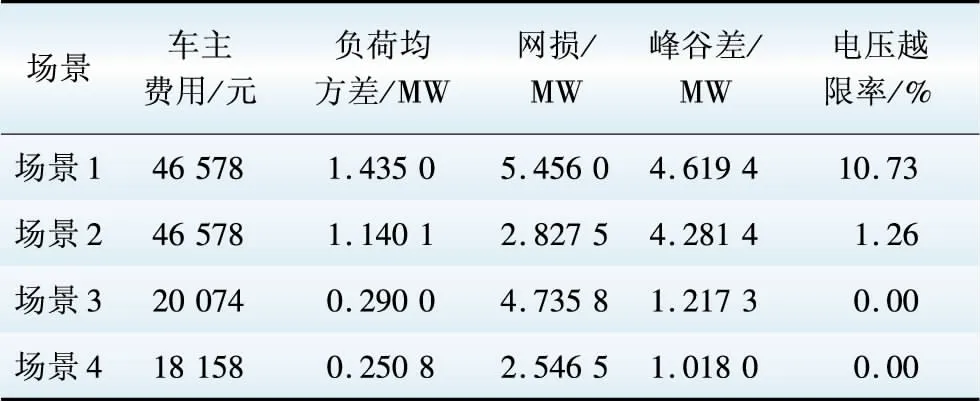
Table4Controleigenvaluesofelectricvehiclesubgroups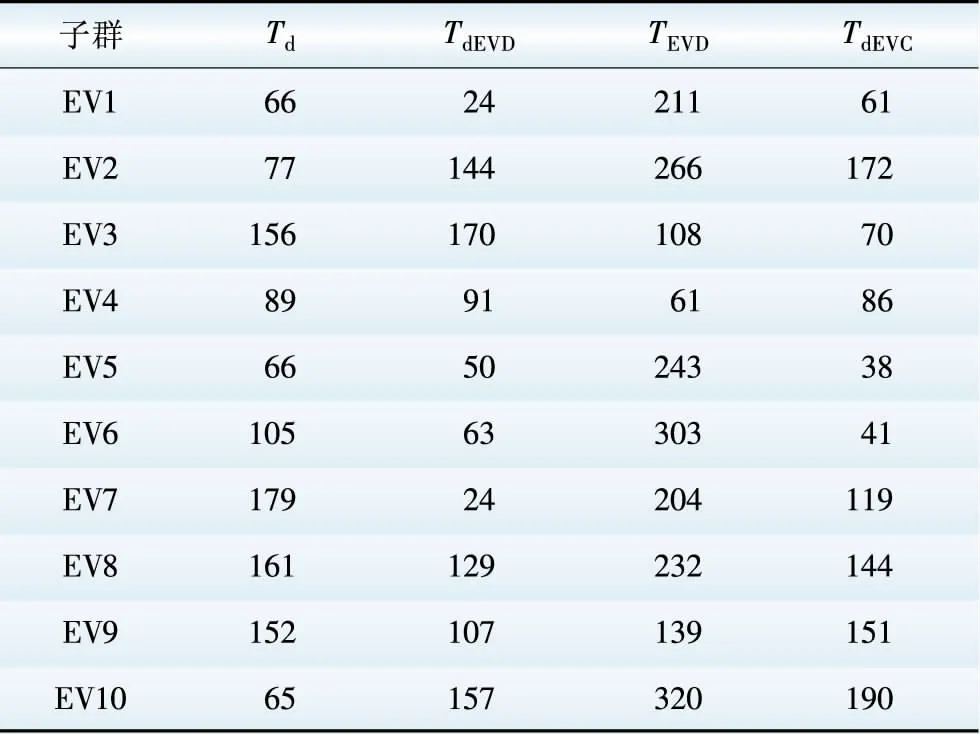
4 结 论
