思维导图在高中数学教学中的应用研究
2018-08-08江苏省如皋市第一中学许金松
☉江苏省如皋市第一中学 许金松
面对高中数学,不少学生都存在着或多或少的学习障碍,对于基础较差的同学来说数学知识尤其难理解、难记忆、难应用,是其通往接受更高等教育道路上亟需克服的困难.思维导图的出现为解决这类困难提供了新的突破点.教师熟悉思维导图,了解应用思维导图开展高中数学教学的优势,可帮助学生打好基础,提高他们对数学知识的掌握能力.
一、思维导图的概念及绘制
思维导图最初由英国著名教育学家、心理学家、英国“记忆力之父”托尼·巴赞创建,他通过研究人类大脑的记忆方式,发明了能够有效帮助人挖掘潜力、提升记忆力的思维工具,即思维导图.思维导图从一个中心主题出发,向外发散出与之关联的各个分支,分支上再产生下一级分支,将所有相关内容,有关中心主题的内涵或外延全部以树状结构的分布显示出来,是一种可清晰模拟出思维方式的示意图.
思维导图由中心主题、分支主题、关联线、关键词、配色和配图六部分组成.绘制思维导图要注意这六个部分的安排.首先思维导图的中心主题是问题围绕的焦点,所有分支都是由中心主题发散而来.中心主题往往绘制成一幅图片,用以加深印象,主题上的文字要突出显示,能够明确主旨.分支主题则是由中心主题发展出来的一系列相关内容,直接发展出来的分支属于一级分支,由一级分支发展出来的属于二级分支,以此类推,分支主题要逐级细化.分支主题的内容对中心主题的内涵起到建设作用,增添新的分支的前提必须是新分支的存在对导图主题概念的丰富具有意义,不要随意增添无关分支.关联线主要是主题与分支主题之间的连接线,在绘制这些连接线时要尽量使用自然弯曲的曲线,而不要用笔直的线,否则思维导图看起来不够生动自然.关键词应当是经过提炼的能够准确概括内容的词,其可以展现点与点之间的联系与思考.在思维导图的配色上,最好不同的分支使用不同的颜色,同一级分支使用相同的颜色,便于分清分支的走向和脉络.最后,适当配图可以减轻观看者的疲惫感,也使思维导图更加直观,易于理解.
二、应用思维导图构建知识体系
应用思维导图进行教学的一大优点是可以轻松构建知识体系,将较为庞大的知识内容和零散的知识内容系统性地串联起来,使人观之条理清晰,一目了然.高中数学知识模块包含的知识点比较多,有些还较为细琐,授课完成后学生很容易感到所学的内容一团乱麻,也容易遗忘部分知识点.思维导图有助于帮助学生拾起这些学海遗珠,梳理所学内容的脉络,系统性地看待数学模块内容.让学生不仅知道学了什么,也知道所学内容的整个结构及发展,这样才能更好地理解掌握,加以运用.
如“三角函数”这一整个模块,其中包括三角函数的基本概念、三角恒等变换及解三角形的内容,在实际教学过程中学生很容易迷惑于数量多、应用情况不同的各种公式,对三角函数的学习产生畏惧心理.教师利用思维导图可以将三角函数的内容铺平了展开在学生面前,清晰地展示三角函数的知识分布,在哪种情况下该用哪种公式,从而破除学生的畏惧心理.
思维导图的应用使原本在学生脑海中较为模糊的概念建立起形象的联系,让学生学习这部分知识内容的时候更有目的性,大大提升了学习的效率.如果学生不知道在学什么,为什么学,学了这些以后可以以之为基础发展什么,就没有办法学好一样东西,应用思维导图的意义正是赋予学生这种学习的动力,让学生看得清楚,学得明白.
三、应用思维导图帮助学生记忆
思维导图通过构建各个关键词之间的联系,更为直接和系统化地展示了事物之间的关系,形成了一种依靠联想效果来加强记忆的网状结构.这种结构对于人们顺利回忆起整片内容有明显的提升效果,因此教师完全可以使用这种方法加强学生对数学知识的记忆能力.让抽象思维不发达,对公式、概念等抽象内容记忆不敏感的学生也能成功提升知识的掌握水平.
在学习了一章的内容之后,教师可以让学生试着画出这一章所学内容的思维导图,将知识模块内包含的知识点一一展现出来.这种方法能够帮助学生记忆知识点,通过自身回忆和思考,列举出来各个知识点之间的联系,发现问题,解决问题.在这个过程中学生逐渐将分散的信息集中起来,自行地归纳学习内容,在加深他们记忆的同时,也有助于找到学习技巧,从此学会学习.
四、应用思维导图整理教学思路
思维导图在教学中的应用除了体现在帮助学生学习和理解,也体现在可以帮助教师整理思路,厘清教学脉络.教与学是一个互动的过程,教师是教的主体,学生是学的主体,缺少任何一个方面,教学效果就不能真正获得提升.然而,教师的教学水平高低是导致大多数学生学习成果优劣的一个重要因素,所以教师还是要认真考虑提升自身的教学能力.思维导图有助于高中数学教师分析教学内容,做好课前学习和备课工作.思维导图的梳理知识点结构和强化记忆等作用同样适用于教师,应用思维导图能为教师整理思路,更合理科学地安排教学提供直观的参考.
课前做好充分的准备是提高教学水平的重要途径,为了做好准备工作,提前整理教学思路、设置课堂环节很有必要.实践证明教师利用思维导图进行教学设计,根据教学思路试安排课堂教学环节,可以更好地完成授课任务.如图1,用思维导图绘制“概率”这一章内容的教学思路:
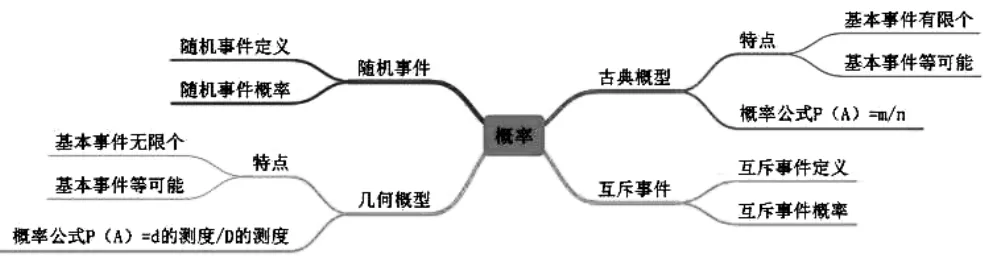
图1
根据思维导图的提示,概率这一章内容的教学主要围绕事件和概型,想要将概率这部分内容讲解明白,就要首先明确事件的分类和定义.事件根据发生的可能性划分为必然事件、不可能事件和随机事件,随机事件是在一定条件下可能发生也可能不发生的事件,必然事件和不可能事件都是能断定的事件,所以我们主要探讨随机事件的概率.而互斥事件则是不可能同时发生的两个事件,如晴天和下雨.所以我们可以得到两个互斥事件A和B的概率公式:P(A+B)=P(A)+P(B);互斥事件中还包含一类特殊的情况,即对立事件,对立事件既互斥,又必然有其中一个会发生.也就是事件A和事件B互斥且事件A不发生的时候事件B一定发生,事件B不发生的时候事
件A一定发生.所以对立事件的概率公式为P(A)=1-P(A).对概型的研究可以帮助我们获得事件发生的概率,古典概型是所有事件只有有限个且每个基本事件发生的可能性都相等的概率模型,在这种情况下,一次试验中某一事件发生的概率等于这一事件中包含的可能发生的基本事件数m与试验可能的基本事件个数n的比值;几何概型的特点则是随机试验中每个基本事件发生的可能性相同,但是试验中所有可能的结果是无限的.一般地,在几何区域D中随机取一点,记事件A为“该点落在其内部一个区域d内”,事件A发生的概率就是d的测度比上D的测度.
思维导图以其发散性思维特点来帮助学生建立知识点之间的联系并对其进行有效记忆,也能使得教师的教学思路更加清晰,课堂教学更加有条理.教师学会应用思维导图进行教学,对学生将来的学习和发展都能起到良好的促进作用.
