基于H P滤波分解的AR M A+BPN N的人民币汇率短期预测

陈东东，沐年国

（上海理工大学 管理学院，上海 200093）

汇率是用一国货币表示另一国货币的价格水平，是一种外汇资产价格水平的货币表现。汇率作为一国重要的宏观经济变量，不仅影响一国宏观经济的运行和微观层次上的资源配置，而且还是维系全球经济发展的一条重要纽带[1]。2015年8月11日，我国汇改又进一步松绑了人民币汇率，使得人民币汇率更加市场化。因此，正确预测人民币汇率的变化也变得越来越重要。

一、研究现状

时间序列分析方法一直是研究汇率的有效并可靠的方法，可以获得观测样本序列产生的随机机制，也就是建立数学模型；亦可以根据在历史数据规律，估算观测样本序列未来的可能取值[2]。由于汇率具有复杂的非线性特征，而ARIMA模型是建立在线性关系的假设上，因此很难有效地捕捉到并解释非线性关系，存在难以调和的矛盾。

神经网络（Neural Networks，NN）具有良好的逼近能力，能挖掘数据背后复杂的非线性特征，是目前非线性系统研究的热门工具之一[3]。Thomas和Yu分别使用BP和RBF非线性神经网络模型对美元汇率进行了短期预测，但由于需要估计的参数较多，导致所模型容易产生数据过拟合，泛化能力不够，从而使其预测精度不高，在短期汇率预测应用中受到了限制[4～5]。

ARIMA模型是基于线性技术来预测的，而对非线性处理效果不佳；NN模型则在挖掘数据背后非线性关系方面有着不可比拟的优势。但汇率市场是复杂演化的动态市场，是高噪声、非平稳的，包含了线性和非线性的混沌系统[6]，因此，使用单一的线性模型或者非线性模型都不能完全描述汇率时间序列的特征。Tseng等人组合ARIMA模型与BP神经网路模型预测季节性时间序列[7]，Yu等结合广义线性自回归模型与NN模型预测汇率[8]，结果显示组合模型的总体预测效果显著优于单一的时间序列模型预测效果。熊志斌采用ARIMA模型预测序列的线性主体，运用NN模型对ARIMA的残差部分进行估计，结果表明融合模型的预测精准率高[9]。

本文在总结前人研究的基础上，将HP滤波分解融合到时间序列ARMA与神经网络（BPNN）组合模型里预测人民币汇率。即采用HP滤波将样本序列分解成平稳趋势项与方差时变的波动项；对平稳序列建立ARMA模型，对波动非线性序列建立BPNN模型，然后将模型的预测值整合，得到样本短期预测值。

二、理论概述

（一）HP滤波

Hodrick-Prescott滤波法把经济运行看作是长期内在的或者潜在的增长趋势和短期波动的结合[10]。该方法采用对称数据移动平均的方法原理，设计了一个滤波器，高频部分通过，低频部分滤除[11]，即HP过滤器是一种将趋势和周期成分从原始时间序列中分离出来的工具[12]，这就是通常意义上的时间序列趋势成分和波动成分[13]。

设一个时间序列Yt表示成：

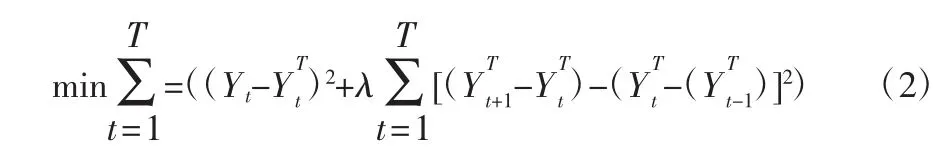
HP滤波依赖于参数λ的设定，该参数λ需要先给定。参数λ是对趋势光滑程度和对原始数据拟合程度的一个权衡参数：随着λ值的增加，估计的趋势越光滑，当λ趋于无穷大时，估计的趋势将接近线性函数。

（二）ARMA模型

ARMA是对平稳时间序列进行自回归AR（p）和滑动平均过程MA（q）建模，并有一整套的建模、估计、检验和控制方法[14]。

模型的表达式：

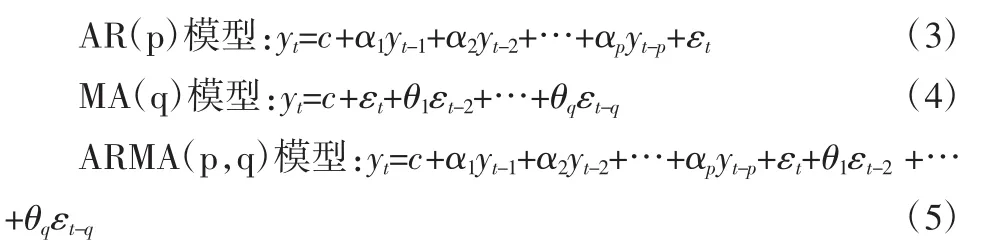
式中：c为常数项，p和q分别表示模型中自回归项和移动平均项的阶数，αi为第i个自回归项的系数；θj为第j个移动平均项的系数；εt为残差项，是独立同分布的随机变量，服从均值为0、方差为1的分布。

（三）神经网络

神经网络是由大量的、简单的处理单元广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学习系统。本文模型通过PSO算法来训练优化神经网络，并最终确定合适的模型参数（Wij和Wj）。PSO算法的基本原理是[9，15～16]：

设在n维的搜索空间中，由m个粒子组成的种群记为：X=（X1，…，Xi，…Xm），其中，第i个粒子的位置为Xi=（Xi1，Xi2，…Xin）T，其速度为Vi=（Vi1，Vi2，…Vin）T。粒子i的个体极值为pi=（pi1，pi2，…pin）T，种群的全局极值为pg=（pg1，pg2，…pgn）T。

粒子在搜索过程中通过跟踪两个目标值来更新自己的速度和位置：一是粒子本身目前找到的最优解，即个体极值；二是整个种群目前找到的最优解，即群体极值。

其迭代公式：

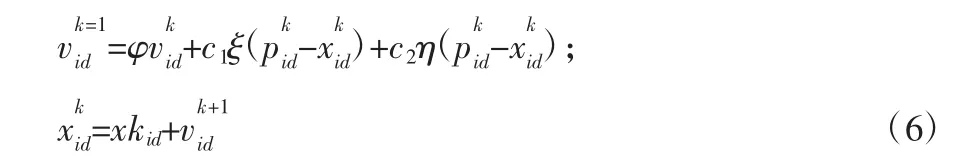
三、实证分析

本文采用了对数据进行HP粗分解方法，首先获得趋势部分和波动部分，然后分别对趋势部分和变化部分建立ARMA、BPNN模型进行预测；同时，对样本数据直接建立ARIMA模型、BPNN模型进样本外预测；然后比较各模型预测值与真实值的均方根误差（RMES）、平均绝对误差（MAE）、平均绝对百分误差（MAPE）和希尔不等系数（TIC）4个常用的预测误差指标。误差指标越小，说明模型的预测值和真实值最为接近，则可判断为最佳模型[17]。

（一）数据来源

本文对人民币汇率进行短期预测，基于何丹青[18]比较大小样本建立ARMA模型效果，证明一些久远的数据不利于ARMA模型的准确预测。因此，本文选择了2013年1月至2017年3月《中国统计年鉴》公布的美元兑换人民币汇率的月度数据为样本，进行分析建立模型，预测汇率走势。

（二）HP滤波分解

先将原始样本数据对数处理，然后用软件Eviews进行HP滤波处理，根据月度数据的趋势性特点，定义平滑指数λ=14 400[19]，结果（如图1所示），平滑虚线Trend代表趋势序列，增长率没有明显的变化；实心圆线Cycle代表波动项，有着周期性的不规则变化。

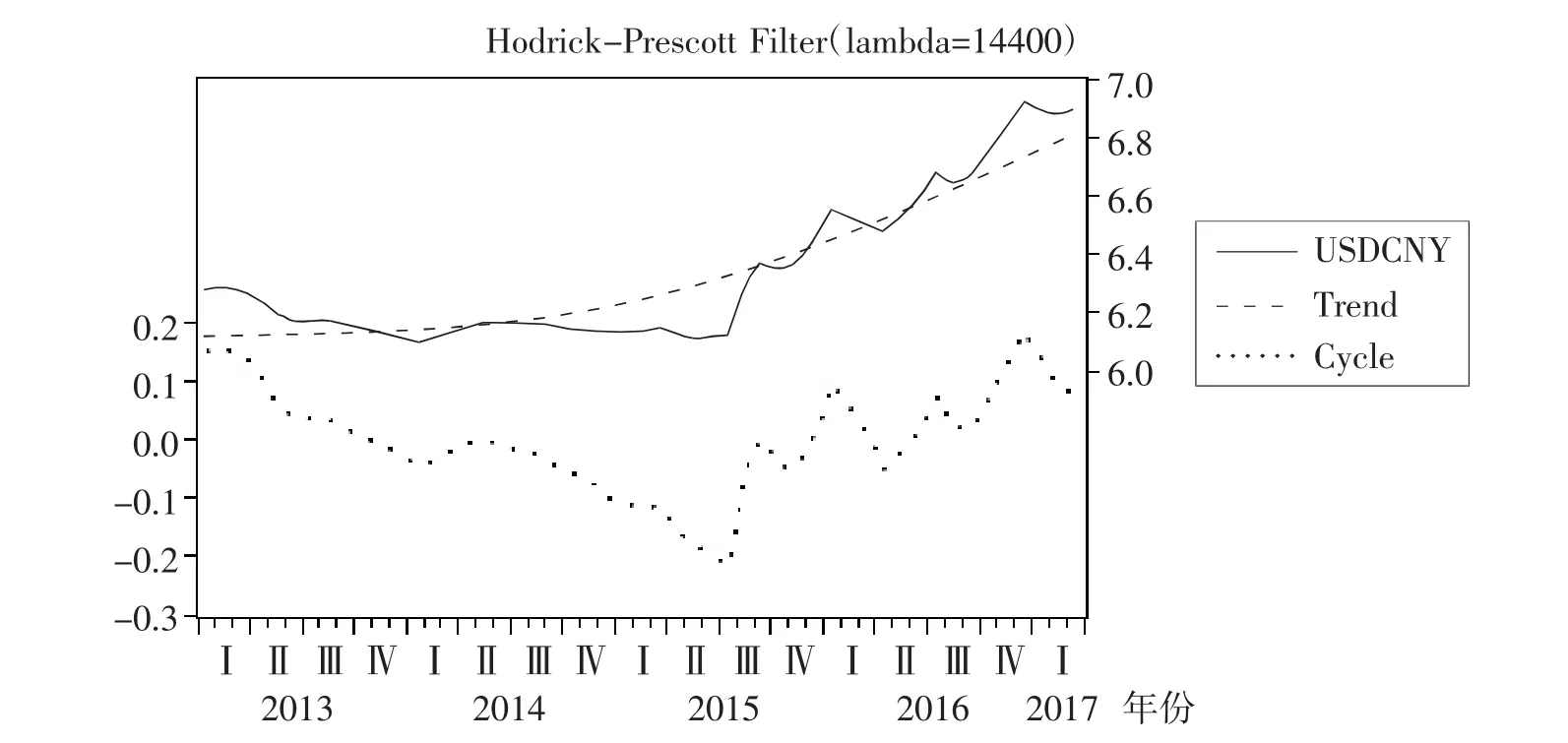
图1 HP滤波分解图

（三）建模

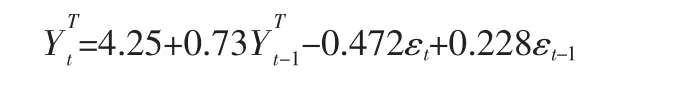
模型程序基于Matlab7.0软件编写并实现。本文采用试错法确定网络输入节点数和隐层节点数，即计算每个粒子所对应神经网络的输出误差，并将该误差作为对应粒子的适应值，找出适应值最好的粒子，将此粒子的位置作为粒子群的群体极值；按照式（6）更新所有粒子位置即产生新的种群；然后计算每个粒子的个体极值进；将每个粒子的个体极值与群体极值进行比较，若更好，则将该粒子的个体极值更新为当前的群体极值；若输出误差满足设计要求，则终止训练并输出结果；否则返回重新计算粒子适应值，直到误差平方和减小到某一目标误差，即认为此算法是收敛的。

经反复试验比较，确定模型为4输入1输出，隐层节点数为5，即网络模型采用4×5×1结构。粒子群算法的各参数选取分别为：c1=1.5，c2=0.2，wmax=0.9，wmin=0.4，vmax=8，vmin=-10，Xmax=10，Kmax=500。利用建模样本对网络训练500代，误差达到0.0091745，训练过程的误差曲线（如图2所示）。

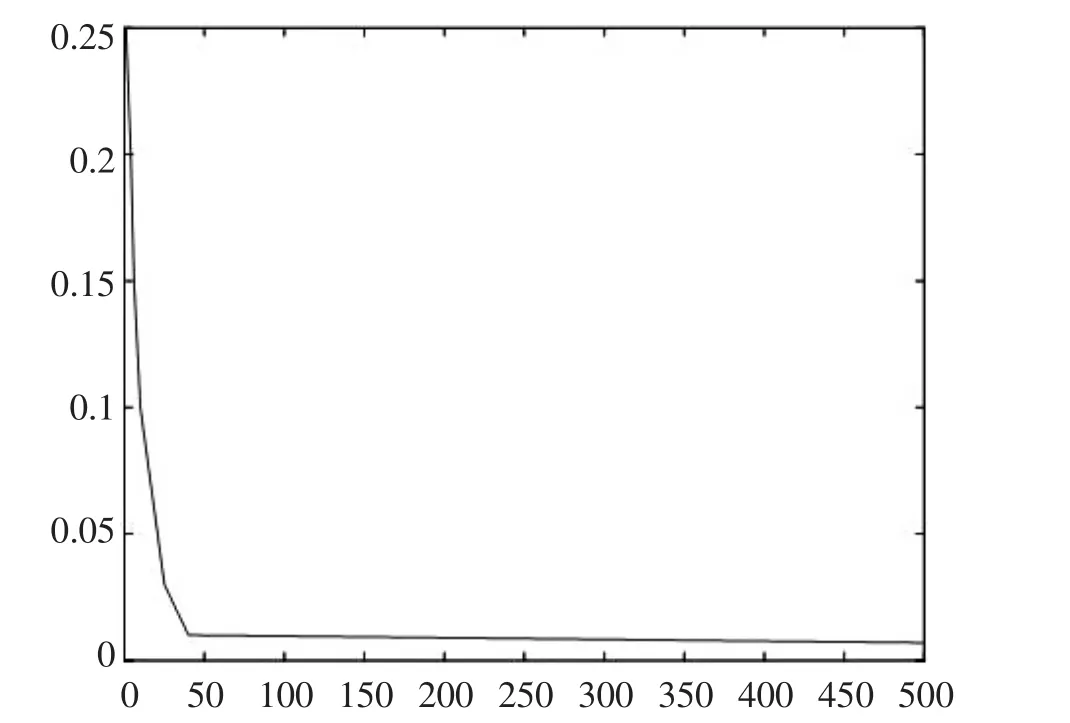
图2 训练误差曲线

3.模型预测值融合。将趋势序列与波动序列模型的预测值整合起来，得到样本序列预测值（如图3所示）。

4.建立ARIMA、BPNN模型。样本数据直接建模进行预测。先进行单位根检验，结果表明样本序列的一阶差分序列为稳定序列；对一阶差分序列建立ARMA，运用Eviews软件，经过多次试设，遵循SC、AIC最小原则确定参数，建立如下模型ARMA（2，2），并进行预测。模型表达式如下：

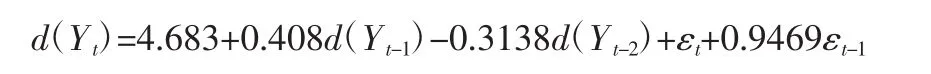
依然采用试错法确定样本序列的网络输入节点数和隐层节点数，建立BPNN并进行预测，预测值（如图3所示）。

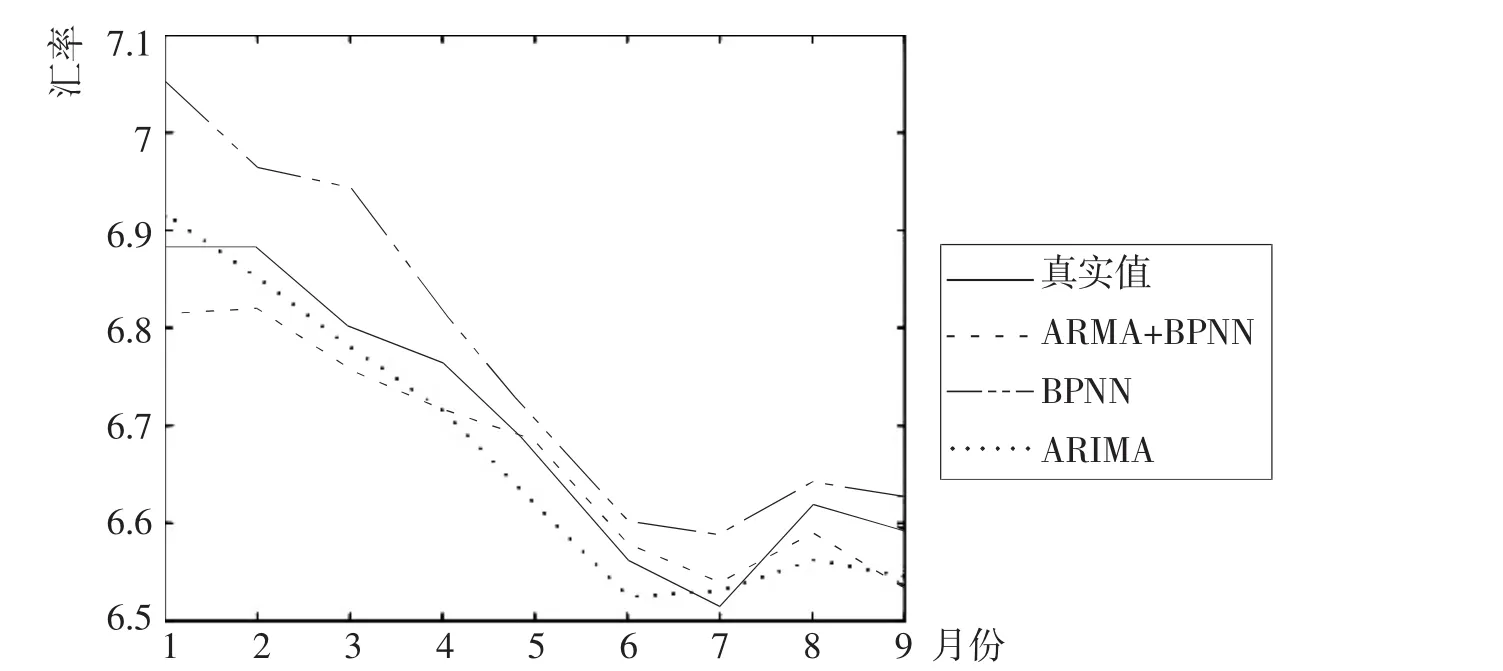
图3 各模型预测值

5.方差分析。为了更加全面地描述不同模型对汇率的预测效果，本文采用4个常用的预测误差指标来衡量模型预测效果，各模型误差指标（如下表所示）。

由上表可知，ARMA+BPNN模型向前短期3个月预测值的各项误差指标值都是最小的，比ARIMA模型的指标值缩小了近6倍，比BPNN模型缩小近20倍；向前6个月预测值的误差指标与ARIMA的相近，比BPNN模型的指标缩小近3倍；但向前9个月的预测值误差指标比ARIMA模型扩大了近2倍，比BPNN模型的指标缩小了近2倍，以上分析说明序列经HP滤波处理后的ARMA+BPNN模型在短期预测精准度得到很大提高。

模型的预测误差指标比较

四、结语

从模型理论上分析，ARIMA模型没有考虑到外界相关因素的影响，导致短期预测效果相对低；而BPNN需要估计的参数较多，导致所得到的模型容易产生过拟合，泛化能力不够，而使其预测精度不高，在短期汇率预测应用中受到了限制；HP滤波分解出趋势项和波动项，既考虑了外界经济长期趋势的影响，也考虑到汇率自身因素，融合了单一模型的长处，更深刻地挖掘汇率序列背后复杂的线性与非线性特征，极大地改善了模型的预测性能。

ARMA善于捕捉数据中的线性特征，而BPNN则擅长挖掘数据背后的非线性关系。融合ARMA-BPNN模型对汇率序列的预测效果都要好于其他单一的模型，这也说明人民币汇率序列不仅具有线性结构特征，也具有非线性特征关系；而融合模型相比单一模型，更能捕捉到人民币汇率的这种复杂的混合特征，极大地提高了模型的预测性能。同时，也表明我国人民币汇率市场并不是一个有效市场，对汇率的预测是有必要的，也是可能的。