基于PVAR模型和VAR模型的工业用水与工业经济增长关系研究
2018-08-07吴凤平张陈俊
史 珍,吴凤平,张陈俊
(1.河海大学企业管理学院,江苏 常州 213022;2.河海大学商学院,江苏 南京 211100)
水资源是国民经济可持续发展的重要资源基础,也是重要的生产要素。1978—2015年,中国工业增加值年均增长率达到11.02%(按照1978年不变价格计算),快速工业化导致资源消耗和环境污染。该时间段内,工业用水量年均增长率达到3.11%,而用水总量的年均增长率仅为0.92%,另外,工业用水量占用水总量的比重由10.30%增加到21.87%,可见,中国工业用水量呈持续增长趋势。中国是水资源短缺的国家,人均水资源量约为2 100 m3,不足世界人均水平的1/3,水资源短缺、水污染严重、水生态恶化等问题十分突出,已成为制约经济社会可持续发展的主要瓶颈[1-2]。因此,针对水资源问题的研究,有利于制定切实可行的水资源政策,也将对水资源消耗总量和强度双控行动的贯彻实施产生重大意义,相关研究也引起了诸多学者的关注。
贾绍凤等[3-4]利用库兹涅茨曲线验证发达国家工业用水随着经济增长而呈倒“U”型形态,并找出工业用水出现转折的拐点,此类研究还有张陈俊等[5]、Katz[6]、张兵兵等[7]、张月等[8]。陈雯等[9]运用指数分解法将工业水资源消耗强度的变化分解为技术进步与产业结构变迁两个层次,此类研究还有陈东景[10]、刘翀等[11]、张陈俊等[12]。姜蓓蕾等[113]分析了工业用水变化及其用水效率的驱动因素。贾绍凤[14]将发达国家工业用水零增长的原因归结为更高的环保要求、产业结构升级和高耗水行业的萎缩,另外,从用水量演变趋势、水价、产业结构升级、环境立法和水资源本身限制5个方面分析中国用水量何时达到顶峰[15]。沈大军等[16]将水资源纳入生产函数,建立数量经济模型,分析北京市工业用水的边际效益、产值弹性。王浩[17]等对我国未来工业需水增长态势进行了趋势展望,同时分流域预测了我国工业经济的未来发展格局及其需水量,提出了保障我国工业经济持续发展的水资源利用对策与措施。邓朝晖等[18]利用VAR模型研究工业用水与经济增长之间的互动关系,此类研究还有张兵兵等[19]、雷玉桃等[20]。
从现有研究可以看出,工业用水与经济增长的关系研究比较丰富,主要包括经济增长及背后隐藏因素对工业用水量的影响,工业用水作为生产要素对经济增长的影响,经济增长与工业用水互动关系研究。从经济增长与工业用水双向互动关系来看,现有研究主要从国家整体、东中西部地区或者单个省份出发,未充分考虑各省份之间的异质性,而我国是一个区域社会经济发展具有显著差异的国家,因此,探讨各省份经济增长与工业用水之间的双向关系有利于制定具有差异化、针对性的工业节水政策措施。
东部地区是中国三大地带之一,包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南等11个省份。2015年东部地区工业增加值占全国工业增加值的比重达到56.14%(当年价格计算),工业用水量所占比重达到46.90%,可见,以东部地区为研究对象具有一定的典型性。
1 模型设置与数据说明
1.1 模型设置
本文采用PVAR模型(Panel Vector Auto Regressive Model)和VAR模型(Vector Auto Regressive Model)分析工业用水与工业经济增长的关系,对两个模型分别进行介绍。
VAR模型是一种非结构化的模型,把系统中每一个内生变量作为系统中所有内生变量的滞后项的函数来构建模型。构建工业用水与工业经济增长的双变量VAR模型,如公式(1)所示:
(1)
式中:yt为双变量的向量,为工业用水与工业经济增长;c是常数项;p是自回归滞后阶数;et为独立同分布白噪声过程。
构建PVAR模型,如公式(2)所示:
(2)
式中:yi,t为双变量的向量,为工业用水与工业经济增长函数,i为省份,t为年份;ηi为地区固定效应,主要反映工业用水与工业经济增长的区域异质性;φi为时间效应,反映时间趋势特征;ei,t为随机扰动项。
1.2 数据说明
本文所用数据的时间跨度为1998—2015年,所涉数据为工业用水量、工业增加值两项指标,数据主要来源于历年《中国统计年鉴》和《中国水资源公报》,对相关指标解释如下:
(1) 工业用水,简称indwater,数据可以从《中国水资源公报》上直接获取。
(2) 工业增加值,简称indav,为了消除价格因素影响,各省份工业增加值以1998年为基期,根据工业生产者出厂价格指数进行调整。
有资料显示,到上世纪八十年代初期,科尔沁草原已经出现四千八百多万亩沙地,通辽市总土地面积已经有五成严重沙化,并以每年十几米的速度向外扩展。而通辽市沙化最为严重的旗县是科左后旗——这令我陷入久久的沉思,我的少年时代就是在那里度过的呀!心,禁不住悲凉起来。
为了避免数据可能存在的异方差和剧烈波动,对工业用水和工业增加值进行对数化处理,分别用lnindwater和lnindav表示。
2 实证分析
2.1 描述性分析
东部地区平均工业用水从1998年的554.18亿m3增加到2015年的626.00亿m3,增加了12.96%,年均增长率为0.85%,与此同时,平均工业增加值从1998年的19 856.04亿元增加到2015年的 154 443.07亿元,增加了6.78倍,年均增长率为12.82%。各省份工业用水与工业增加值的变化趋势却存在较大的差异性,如图1所示,工业增加值均呈上升趋势,而工业用水却呈现出不同的变化特征。
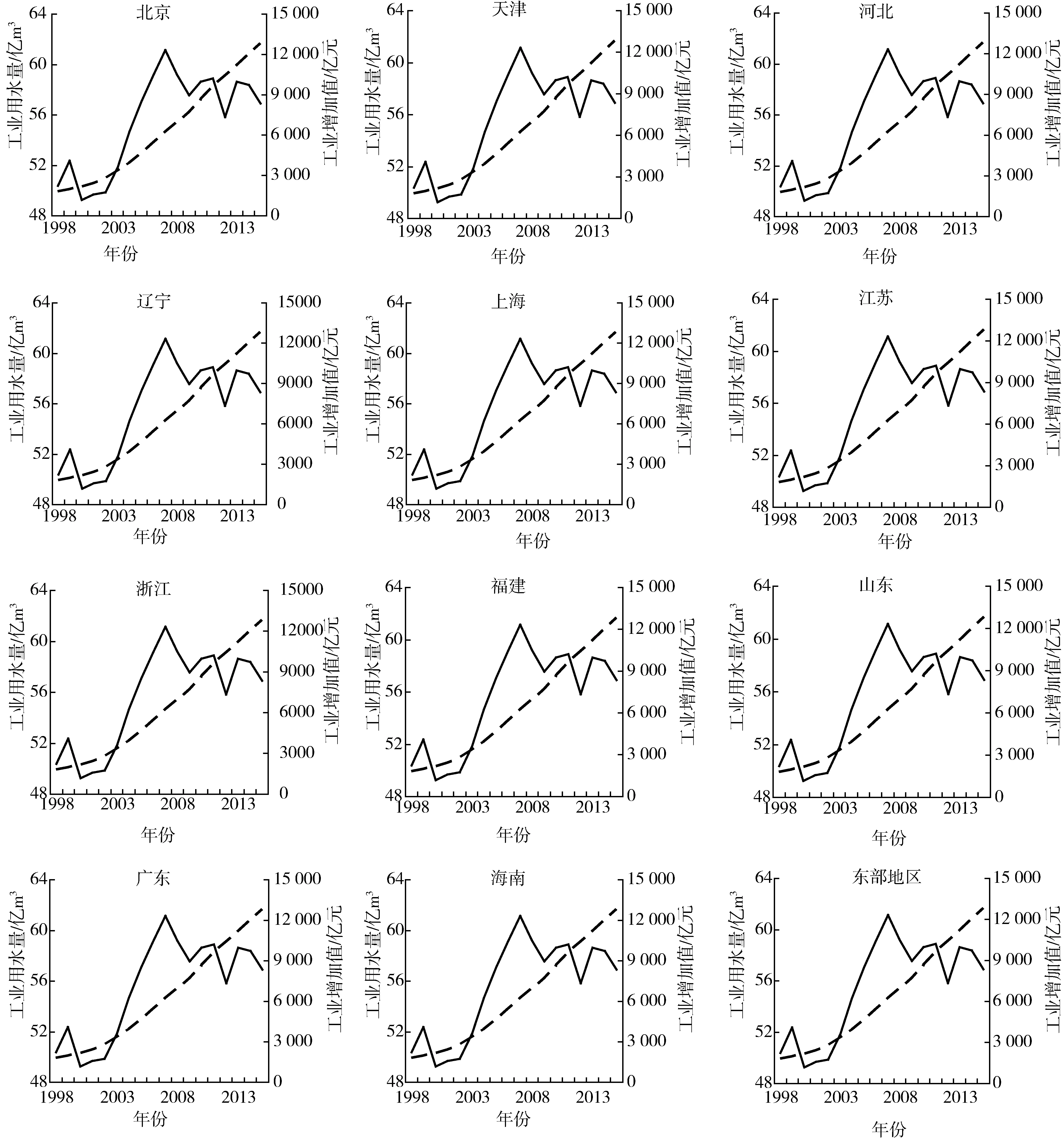
注:实线、虚线分别表示工业用水量和工业增加值。图1 东部省份工业用水与工业增加值变化趋势
表1显示了东部地区及所属11个省份工业用水与工业增加值的描述统计结果,可以看出省份之间的较大差异,进一步说明研究各省份工业用水与工业经济增长关系的必要性。
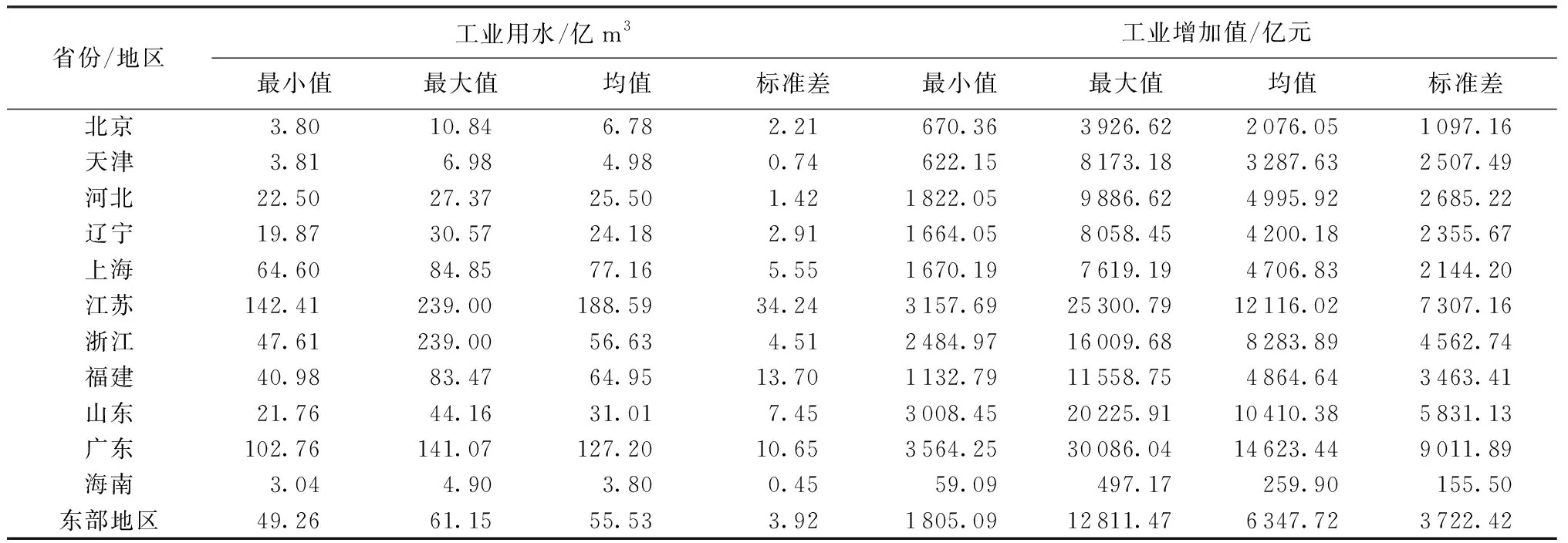
表1 东部地区及省份工业用水与工业增加值描述统计结果
2.2 PVAR模型
从单位根检验、协整检验、PVAR估计、脉冲响应分析以及预测方差分解5个部分开展PVAR模型研究。
2.2.1 单位根检验
在建立PVAR模型之前,需要对序列平稳性进行检验,为了保证检验结论的稳健性,分别列出了五种检验方法所得结果,检验结果如表2所示。工业用水和工业增加值水平值所有检验都不显著,因此不能拒绝“存在单位根”的原假设,说明序列是不平稳的,需要对变量的一阶差分项进行检验,所有检验都在1%水平下显著,因此,拒绝“存在单位根”的原假设,可以认为工业用水与工业增加值都是一阶单整序列。

表2 面板单位根检验结果
注:*、**、***分别表示在10%、5%和1%水平下显著,下同。Dlnindwater、Dlnindav分别表示变量的一阶差分
2.2.2 协整检验

表3 面板协整检验结果
2.2.3 PVAR估计
表4显示了工业用水与工业增加值PVAR模型估计结果,从AIC、BIC和HQIC 3个统计量可以判断出模型M2更优。从M2中看出,方程工业用水中,工业用水的滞后一期在1%水平下显著且系数为正,说明当期工业用水受到上一期的正向影响;方程工业增加值中,工业用水的滞后一期在5%水平下显著,说明工业用水对工业经济增长有显著的正向影响,水资源是工业生产过程中不可缺少的重要生产要素,工业增加值的滞后一期在1%水平下显著,说明当期工业增加值也受到上一期的正向影响。将M2的变量系数与M1相比,可以发现全部系数都有所上升,并且显著水平基本相同,可以得出两个模型并不矛盾,而是相互补充。

表4 工业用水与工业增加值的面板VAR模型
注:M1表示滞后一期,M2表示滞后二期,括号内的值为t统计量值。感谢世界银行Love博士提供的PVAR程序[22]以及中山大学连玉君老师提供的PVAR2程序。N表示样本量,AIC、BIC和HQIC是用于判断滞后阶数的准则,阶数的确定应该以上述三者最小为准
2.2.4 脉冲响应分析
脉冲响应函数描述一个内生变量对误差冲击的反应,具体来说,它描述的是在扰动项上施加一个标准差大小的冲击后对内生变量当期值和未来值所带来的影响,笔者将冲击响应期设定为10期,图2(a,b,c,d)显示了工业用水与工业经济增长的脉冲响应分析结果。从工业用水对自身扰动的响应(图2a)来看,随着时间的推移,响应值在逐渐下降。从工业用水对工业增加值扰动的响应(图2b)来看,当期为0,第一期为0.008 4,第二期为0.008 8,随后就逐步下降,但是在分析期内始终是正值,说明两者是正相关关系。从响应来看,随着工业经济增长,工业用水经历着先上升后下降的过程,近似呈倒“U”型形态,主要因为工业增长过程中会伴随着行业结构优化和节水技术进步,减少水资源消耗,图1也显示了此特征,与雷玉桃等[17]的研究结论具有相似性,只不过研究对象是全国时间序列数据,下降的时期为第7期,因为全国平均工业增加值要落后于东部地区。从工业增加值对工业用水扰动的响应(图2c)来看,当期为0.010 5,一直增加,第5期达到最大,为0.058 7,随后下降,在分析期内也始终为正值,说明工业用水与工业经济增长是正相关关系,但是水资源作为生产要素对工业经济增长的作用却逐渐减弱,开始制约工业经济增长,主要因为水资源的稀缺性,因此需要进一步提高工业用水效率缓解水资源压力。从工业增加值对自身扰动的响应(图2d)来看,当期为0.065,第1期达到最大0.066 4,随后一直下降。
2.2.5 预测方差分解
预测方差分解的主要思想是把系统中每个内生变量的预测均方误差按其成因分解为与各方程相关联的几个部分,从而得出对模型内生变量的相对重要性。表5显示了第10、20、30期的方差分解结果,可以得到工业用水的波动主要来自自身,但是呈缓慢下降的态势,在第11期达到稳定,为98.0%;工业用水对工业增加值的影响在逐渐增加,但是增加的速度在不断放缓,与此对应,工业增加值对自身的影响在不断下降,由此说明工业用水与工业经济增长的关系越来越密切,由于受困于水资源稀缺的现状,需要通过工业内部结构优化、节水技术创新等途径提高用水效率,从而缓解水资源对工业经济增长的制约。
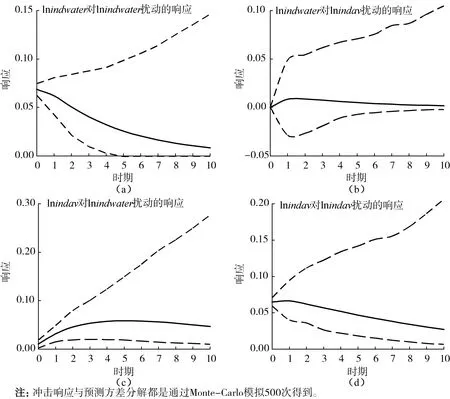
图2 工业用水与工业增加值的冲击响应

时期对工业用水的方差分解对工业增加值的方差分解lnindwaterlnindavlnindwaterlnindav100.9810.0190.4870.513200.9800.0200.5490.451300.9800.0200.5550.445
注:由于篇幅限制,只列出第10、20、30期的分解结果。
2.3 各省份VAR模型
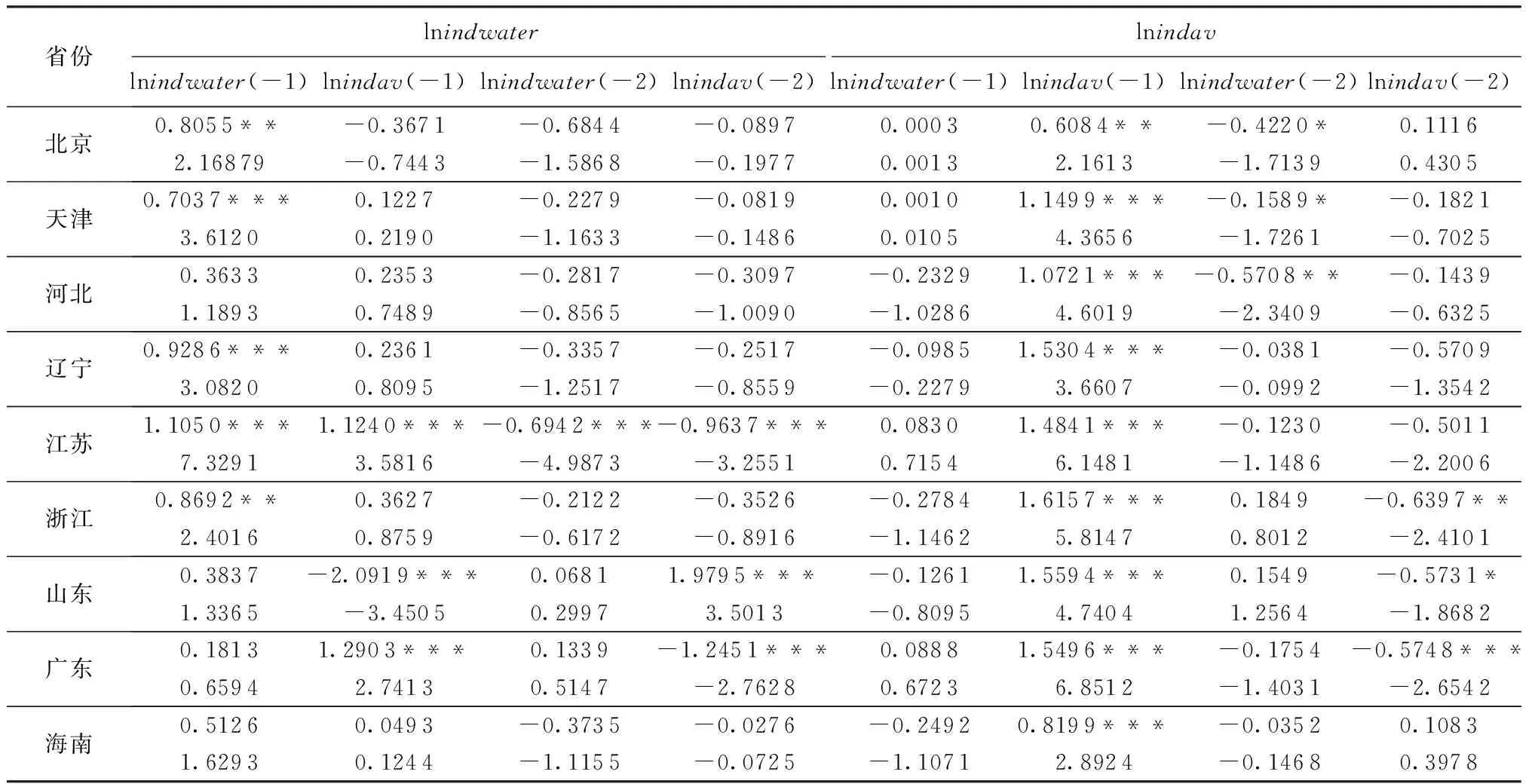
表6 东部地区部分省份VAR模型估计结果
注:常数项没有列出,各省份第二行数据是t统计量值。
各省份工业用水与工业经济增长互动关系研究思路与PVAR模型相同,在建立VAR模型之前,需要对序列进行单位根检验和协整检验。通过单位根检验中的ADF检验发现,只有山东和海南的工业用水和工业增加值序列是一阶单整,其他省份都是非同阶单整。随着协整理论的发展,对于非平稳时间序列,只要各变量之间存在协整关系也可以直接建立VAR模型[23]。通过协整检验发现,11个省份工业用水与工业经济增长之间都存在协整关系,对VAR模型进行平稳性检验发现,上海和福建的VAR模型的根模的倒数不是全部位于单位圆内,因此模型是不稳定的。综上所述,上海和福建两省份不能建立VAR模型,表6显示了北京、天津等9个省份的VAR模型估计结果。估计结果存在较大的差异性,验证了分省研究的必要性,从表6中可以得到如下结论:江苏、山东和广东滞后一期和滞后二期的工业经济增长对工业用水影响的系数均在1%水平下显著,但是方向存在差异性;仅有北京、天津、河北滞后二期的工业用水量对工业增加值影响的系数显著。

图3 lnindwater对lnindav扰动的响应

图4 lnindav对lnindwater扰动的响应
图3和图4分别显示了9个省份工业用水对工业增加值扰动的响应以及工业增加值对用水扰动的响应。可以得到如下结论:①不论工业用水对工业增加值扰动的响应,还是工业增加值对工业用水扰动的响应,各省份都存在较大的差异;②随着时间推移,北京、河北、辽宁、江苏、浙江、广东工业用水对工业增加值扰动的响应最终处于0值以下,其中北京始终处于0值以下,说明在观察期内,经济增长促进了工业用水的下降,而天津、山东和海南工业用水对工业增加值扰动的响应最终处于0值以上,其中,天津和海南始终处于0值以上,说明经济增长导致工业用水的上升;③除了辽宁、浙江和广东外,其他省份随着时间推移,工业增加值对工业用水扰动的响应最终都处于0值以下,说明水资源对工业经济增长产生制约作用,仅是出现的时期存在差异而已。
表7显示了9个省份的预测方差分解结果,列出第10期、20期和30期的结果,可以得出如下结论:不论是工业用水,还是工业增加值的方差分解结果,各省份存在较大的差异,这与区域社会经济发展差异有关,20个预测期和30个预测期的分解结果差距较小,说明20期后,系统基本趋于稳定;工业增加值对工业用水的贡献中,江苏达到60%以上,山东和广东分列第二、三位,需要转变工业经济增长方式,各省份的贡献均普遍上升,但上升的幅度存在差异,说明工业经济增长增加了对水资源的需求;工业用水对工业增加值的贡献中,天津和河北的贡献有所提高,剩下的省份都有所下降,说明水资源作为生产要素,对工业经济发展的作用有所降低。
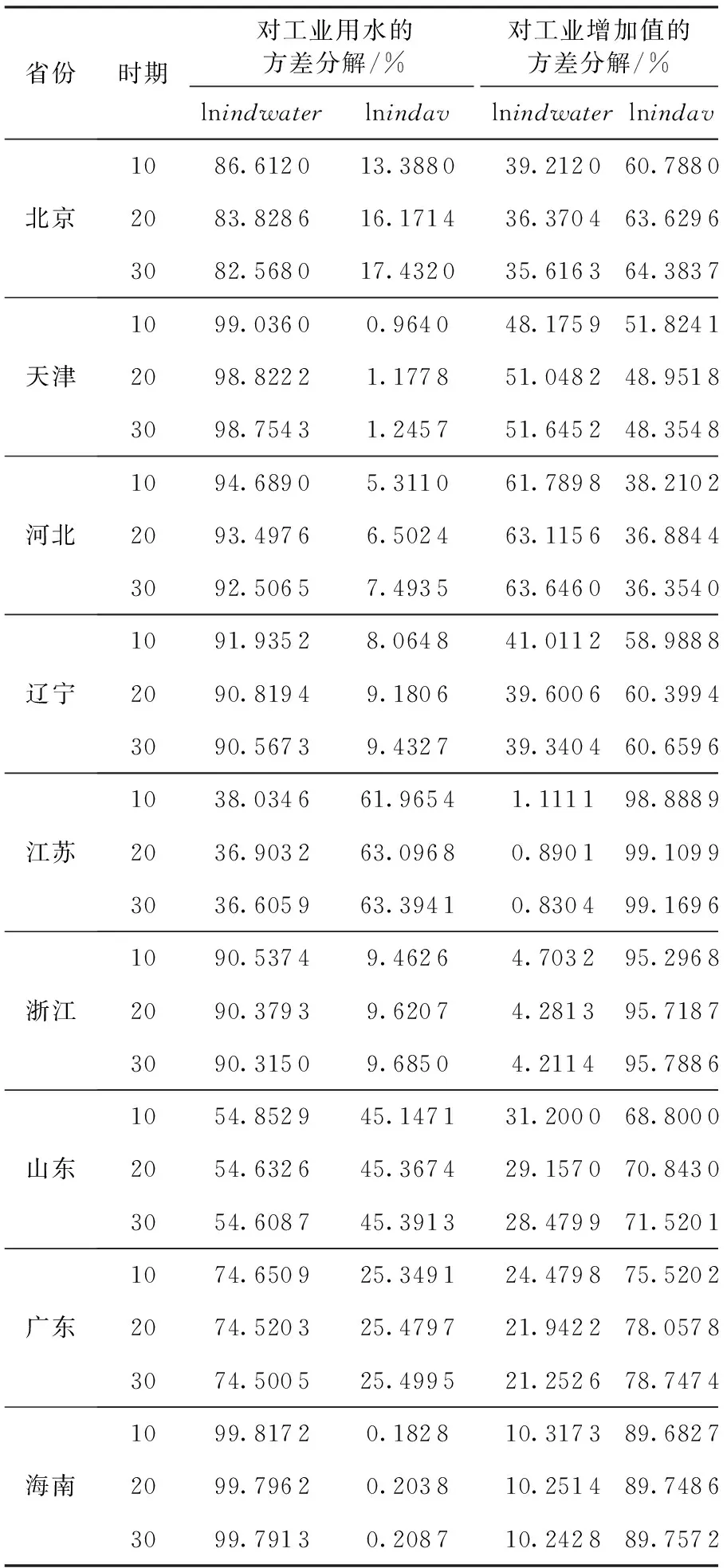
表7 工业用水与工业增加值的方差分解
3 结论与建议
本文以东部地区为例,分别建立PVAR模型和VAR模型,研究东部地区整体以及各省份工业用水与工业经济增长之间的相互影响关系,得出如下结论:
a. PVAR模型估计结果。工业用水与工业增加值滞后一期都对各自当期值有正向影响,同时,工业用水的滞后一期对工业经济增长有显著的正向影响,滞后二期模型M2与滞后一期模型M1并不矛盾,而是相互补充的关系。脉冲响应分析显示,随着工业经济增长,工业用水经历先上升后下降的倒“U”过程,与工业内部结构优化与节水技术进步等密切相关,而水资源作为重要的生产要素,对工业经济增长的作用却逐渐减弱,开始制约工业经济增长。预测方差分析得到工业用水的波动主要来自自身,却呈现缓慢下降的态势,工业经济增长受到工业用水的影响在逐渐增加,但是增加的速度有所放缓,说明水资源已经制约到工业经济增长。
b. VAR模型估计结果。除上海和福建外,剩下9个省份的VAR估计结果存在较大的差异。江苏、山东和广东滞后一期和滞后二期的工业经济增长对工业用水的影响显著,但是方向存在差异性;仅有北京、天津和河北滞后二期的工业用水对工业增加值影响的系数显著。脉冲响应分析显示,除辽宁、浙江和广东外,其他省份的水资源将陆续对工业经济增长产生制约作用,北京、河北、辽宁、江苏、浙江和广东工业经济增长最终将促进了工业用水的下降,而其他省份将最终促进工业用水的上升。预测方差分解得到20期后系统趋于稳定,工业增加值对工业用水的贡献普遍上升,天津和河北的工业用水对工业经济增长的贡献有所上升,其他省份却下降。
基于以上结论,提出如下政策建议:①由于各省份社会经济发展存在较大的异质性,PVAR模型与VAR相结合是必要的,面板数据模型与地区时间序列模型相结合同样可以推广到用水量与经济增长的其他研究中;②努力提高工业用水重复利用率,需要严格管控电力行业、化工行业、钢铁行业、非金属矿制品行业、石油化工行业、食品行业、造纸行业和纺织行业等高耗水行业的发展,提高工业水资源利用效率,缓解工业用水对工业经济增长的制约;③兼顾工业经济发展速度与质量,权衡工业经济增长与水资源利用之间的关系,争取实现工业用水量的零增长或负增长;④各省份工业用水量与工业经济增长的关系存在较大差异,因此需要根据各省份工业用水与工业经济增长的不同结论,因地制宜制定不同的水资源政策。
