基于IUPF的锂离子电池剩余使用寿命预测方法

李丽敏,温宗周,宋玉琴

(西安工程大学电子信息学院,陕西 西安 710048)

0 引 言

国家在“十三五”规划中明确表示新能源将被大力发展，电能的使用将逐渐替代其他相关能源，如汽油等[1]。因此，储能原件如电池的应用将更加广泛，而锂电池因其相同体积下较其他电池储电更多而被大量使用，如电动汽车、小型无人机等均采用锂电池供电方式[2-3]。在享受电动装置带给人类方便时，锂电池寿命预测显得尤为重要，若锂电池已达寿命临界值而没有及时更换，失电的用电设备会突然停止运行，造成比较严重的后果[4]。文献[5-16]中综述了当前国内外关于锂电池寿命预测方面的研究现状。目前，锂电池寿命预测算法包含2大类：

一类是基于模型的方法。该类方法的应用前提是已知对象模型，一旦模型已知，便能精确预测。问题是，目前很多非线性系统的模型未知，则比较难实施[5-9]。如文献[10]提出将耦合数值方法应用于电动汽车的锂电池寿命预测，前提是必须已知该电池的模型，才能继续开展后续工作。

另外一类是基于数据驱动的方法。原理是从数据中总结出规律然后再进行预测，事实证明该类方法鲁棒性比较差[11-17]。

粒子滤波(PF)方法能够将上述2类方法有效进行融合，既吸收了基于模型预测方法准确性方面的优点，也改进了数据驱动方法鲁棒性不强的缺点，是目前应用最多的一种预测方法，其在本文中的应用提升了锂电池寿命预测的准确性。粒子滤波方法起源于Monte Carlo方法，用粒子集来表征概率，可以用于任何形式的状态空间模型上[18-25]。为准确估计锂离子电池剩余使用寿命，将粒子滤波方法进行改进后，得到改进的无迹粒子滤波方法(IUPF)，用于锂电池剩余使用寿命的计算。之所以采用改进的无迹粒子滤波方法原因是，一般的无迹粒子滤波方法在计算UT变换之前，其输入值协方差矩阵Pt-1是奇异值时，会导致UT变换结果无效，因此本文在采用无迹粒子滤波方法时，首先对协方差矩阵Pt-1进行了奇异值分解，获得了等效的特征值表达，再重新进行UT变换，使得预测结果更加准确。

1 UPF算法概述

UPF算法是PF和无迹卡尔曼滤波(UKF)算法的融合，在标准的PF算法中，动态状态空间方程如式(1)和式(2)所示[26]。

xt=f(xt-1,vt-1)

(1)

yt=h(xt,nt)

(2)

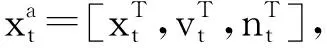
(3)

(4)

(5)

(6)

2)在t=1,2,...时刻。循环下列步骤：

2.1)重要性采样。

①根据公式(7)计算sigma点：

(7)

其中，λ=α2(nx+κ)-nx，α和κ为尺度参数。

②xt迭代。

③yt迭代。

④估计重要性权值。

⑤归一化重要性权值。

2.2)选择(同PF方法)。

2.3)输出结果(同PF方法)。

2 IUPF算法及其在锂离子电池寿命预测中的应用

2.1 IUPF算法

(8)

其中，U为左奇异向量，S称为奇异值矩阵，V是右奇异向量。分解过程为：

①求协方差矩阵P的转置PT；

②求PTP的特征值λi：(PTP)Vi=λiVi；

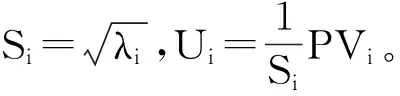
2)计算sigma点。

(9)

(10)

2.2 仿真验证

在仿真验证部分，主要从2方面开展:1)采用3种标准评价本文方法在估计锂电池寿命预测时是否满足要求；2)与UPF方法在上述3种指标下进行预测准确度的比较。选择美国宇航局(NASA)艾姆斯预测数据库公布的锂离子电池容量数据[27]作为测试集，选取其中2组电池的容量数据进行算法性能的测试。

1)锂电池模型的建立和参数初始化。

根据文献[25]所述的锂离子电池退化模型如式(11)所示，将其作为锂电池寿命预测的基础。

Cap=a·exp (b·t)+c·exp (d·t)

(11)

式(11)中，Cap为锂离子电池容量(Ah)，参数a、c是与内阻相关的2个参数，b、d是与锂电池性能退化速率相关的2个参数，t为锂电池循环充电次数。如果a、b、c和d这4个参数可以被准确地估计，则锂离子电池的容量值也能够被准确地估计。

2)锂电池剩余使用寿命计算。

(12)

(13)

(14)

3)3种评价指标。

为综合评价算法的性能，选择了以下3个指标，如表1所示。

表1 3种评价指标

评价指标名称具体公式估计误差Est_error=∑mi=1Cap(i)-Cap_real(i)Cap_real(i)均方根误差(RMSE)均值A=∑mi=1(Cap-Cap(i))2RMSE_mean=A均方根误差(RMSE)方差RMSE_var=∑Ni=1(A(i)-A)N

4)仿真结果。

①第一组数据仿真结果。

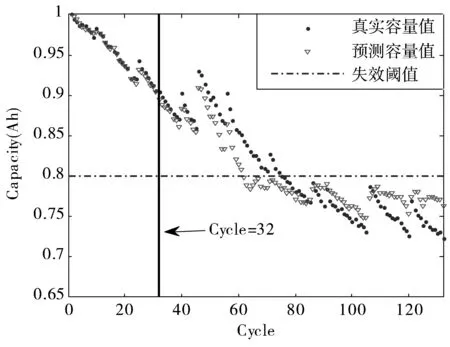
(a) UPF

(b) IUPF

如图1所示，以32充电次数前的数据作为训练数据，以其后数据作为测试数据，结果表明IUPF方法预测出的容量值结果优于UPF方法，这为准确计算锂电池剩余寿命提供了基础。

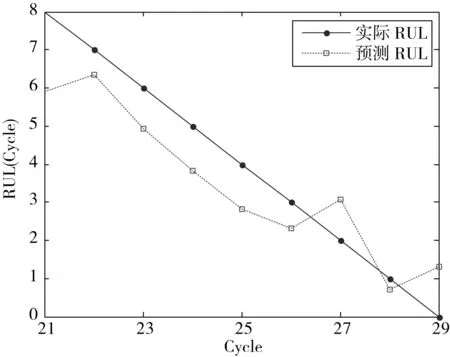
在预测出的容量值的基础上，利用式(14)计算锂电池剩余使用寿命，结果如图2所示。

(a) UPF

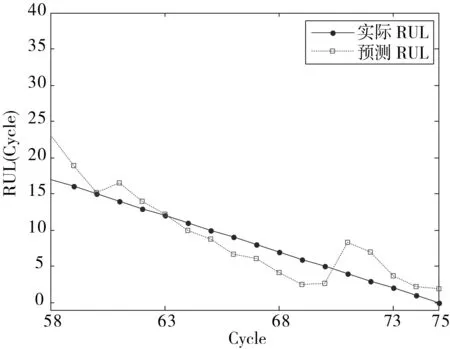
(b) IUPF

从图2可以看出，IUPF方法计算得到的RUL结果更加贴近于实际的RUL，为将评价结果量化，采用表1中的3种评价指标进行性能对比，如表2所示。

表2 第一组测试数据对2种方法进行的3种评价指标比较

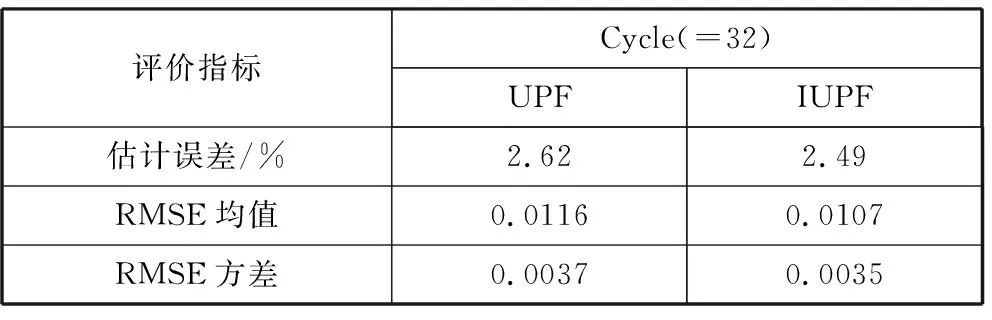
评价指标Cycle(=32)UPFIUPF估计误差/%2.622.49RMSE均值0.01160.0107RMSE方差0.00370.0035

②第二组数据仿真结果。

(a) UPF

(b) IUPF

(a) UPF

(b) IUPF

如图3所示，以12充电次前的数据作为训练数据，以其后数据作为测试数据，结果表明IUPF方法预测出的容量值结果同样优于UPF方法。

从图4看出，IUPF方法计算得到的RUL结果更加贴近于实际的RUL，为将评价结果量化，采用表1中的3种评价指标进行性能对比，如表3所示。

表3 第二组测试数据对2种方法进行的3种评价指标比较

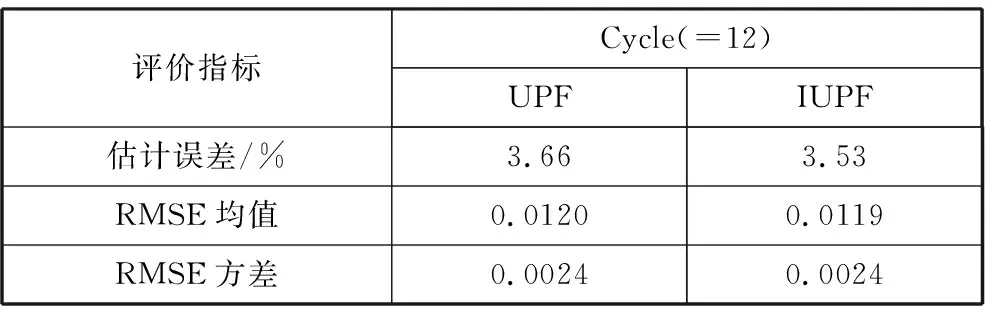
评价指标Cycle(=12)UPFIUPF估计误差/%3.663.53RMSE均值0.01200.0119RMSE方差0.00240.0024

从表2和表3的对比结果可以得到结论，基于IUPF的锂电池寿命预测方法总体性能优于UPF方法，验证了本文方法的有效性和优越性。

3 结束语

针对锂离子电池寿命预测，本文在无迹粒子滤波方法的基础上，对求解sigma点用到的协方差矩阵先进行奇异值分解，提升该算法的鲁棒性，从而提升了锂电池寿命预测性能。采用美国宇航局(NASA)艾姆斯预测数据库中的锂离子电池容量数据作为测试数据，经过多组数据的仿真测试，验证了IUPF算法在用于锂电池剩余使用寿命时优于UPF算法。