基于开口度和扭转角的吊钩形变检测算法
2018-08-07吴良成
吴良成,郭 玲
(南京理工大学自动化学院,江苏 南京 210094)
0 引 言
在传统方法中,吊钩开口度、危险磨损断面以及扭转变形等尺寸变化,采用如游标卡尺、千分尺、卡钳等检测,测量方法看似简单,在实际操作中却存在问题,比如吊钩扭转变形,必须把吊钩拆下,在专用平台上用划线法测得。在传统测量方法中,工具的差异将导致结果误差较大,很难对吊钩几何尺寸变化进行迅速、准确的报废判断。由于吊钩的报废标准主要是检测吊钩的开口度、危险磨损断面以及扭转变形等尺寸,所以吊钩的几何尺寸测量在其检测中是重中之重。在起重机械安全规程中规定,当吊钩出现下列情况之一时[1],应予以报废:
1)吊钩存在裂纹。
2)危险断面磨损达原尺寸的10%。
3)开口度比原尺寸增加15%。
4)扭转变形超过10°。
5)危险断面或吊钩颈部产生塑性变形。
6)当板钩衬套磨损达原尺寸的50%时,应报废衬套。
7)当板钩心轴磨损达原尺寸的5%时,应报废心轴。
本文从完整吊钩三维点云数据[2-3]着手,首先根据基于随机采样一致性的算法[4]对点云模型进行分割,获取钩柄圆柱模型;对圆柱模型进行中轴提取得到单位方向向量以及其上一点;采用点云分割算法[5]以及对称面提取算法,获取吊钩形变以及不形变部分的对称面来计算扭转角;根据圆柱中轴与吊钩的交点以及中轴单位方向向量与垂直于钩柄对称面的向量决定的平面,获取开口度的2个参照点来计算开口度的大小,完成吊钩的形变检测[6]。
1 算法总体流程
针对吊钩形变检测中的开口度以及扭转角,提出一种综合点云圆柱分割、圆柱中轴提取以及基于主元分析法(Principal Component Analysis, PCA)的模型对称面提取来计算开口度以及扭转角的算法。该算法的流程如图1所示。

图1 算法流程图
2 关键算法介绍
2.1 圆柱中轴提取算法
开口度是吊钩形变检测中的一个重要的标准,按照国家标准,当吊钩的开口尺寸超过未使用时尺寸的15%时,此吊钩应报废。传统的人工检测方法中,开口度的检测[7]为:在刚启用新的起重机吊钩时,在钩身开口的两侧各冲出一个小孔,测量2孔的距离并将其记录在案,用来与日后起重机吊钩变形后的尺寸进行比较,以此判断开口度变化的程度。在本文中,同样需要找出2个参照点来计算吊钩的开口度,但作为一个高度自动化的系统,不使用人工选点的方式来选择参照点,需要运用算法的方式来查找参照点,这是开口度测量中的难点。在这个算法中,用到了圆柱的中轴提取算法,以下进行着重介绍。
在三维坐标系中,要知道圆柱的中轴,只要知道轴线上的一点,以及轴线的方向向量就可唯一确定这一条轴线[8-9]。求解圆柱中轴的计算步骤如下:
1)求解圆柱轴线单位方向向量。
由于圆柱表面的点到轴线上的距离是相等的,依据最小二乘原理,使得圆柱面上的点到拟合轴线距离的平方和最小:
(1)
其中di为测量点(xi,yi,zi)到拟合轴线的距离,(l,m,n)为轴线的单位方向向量。
通过转化可将式(1)展开成式(2):
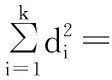
(mδz-nδy)]+f(l,m,n)
(2)
其中:
f(l,m,n)=(1-l2)B11+(1-m2)B22+(1-n2)B33-
2lmB12-2nlB13-2mnB23
(3)
因此对任意的l、m、n都有:
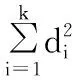
(4)
由式(4)可知优化问题式(1)的最优解与式(5)所述优化问题的最优解相同。
(5)
引入矩阵B=[Bij],则:
f(l,m,n)≥B11+B22+B33-λmax(B)
(6)
文献[10]中指出当且仅当[l,m,n]T为矩阵B的最大特征值λmax(B)对应的单位特征向量时式(6)可以取最小值,这个单位特征向量即为圆柱轴线单位方向向量[11]。但在实际测试中,当圆柱垂直于3个坐标平面时λmax(B)对应的并不是轴线单位方向向量。故在其基础上修改为,若求得3个特征向量中有某个值大于0.99的向量为所求向量,若没有,则为最大特征值λmax(B)对应的单位特征向量。
2)转换原始坐标系。
假设测量数据(xi,yi,zi)所在的坐标系为o-xyz,对(xi,yi,zi)进行坐标变换,设变换后的坐标系为o-x′y′z′,使得z′轴与轴线单位向量[l,m,n]重合,其旋转变换矩阵R为:
(7)
则新坐标系中的点(x,y,z)的计算为:
(x,y,z)T=R×(xi,yi,zi)T
(8)
此时的圆柱垂直于oxy平面,在oxy平面上投影为一个圆。故可以只考虑x、y的坐标,使用最小二乘法求解这个圆的半径和圆心坐标。然后对圆心坐标进行坐标反变换即可求得圆柱轴线上一点。
3)根据坐标转换后的坐标求解投影圆的半径和圆心。
由转换后的圆柱面在oxy平面上的投影为圆[12-13],设最小二乘法拟合曲线为:
(x-a)2+(y-b)2=r2
(9)
令:
(10)
设圆柱面上的点数为N,则令:
(11)
由最小二乘的方法可解得:
(12)
即:
(13)
由式(11)、式(12)和式(13)可计算出由转换后的圆柱面在oxy平面上的投影所拟合的圆的圆心坐标(a,b,0)以及半径r的大小。
4)对步骤3求得的圆心坐标进行坐标反变换得到圆柱轴线上一点。
步骤3中求得了变换后的拟合圆的圆心坐标(a,b,0),这个圆心就是圆柱面中轴上的一点,由此进行坐标反变换即可得到原坐标系中圆柱中轴线上的一点,设这个点为(x′,y′,z′),则有:
(x′,y′,z′)T=R-1×(a,b,0)T
(14)
由此,即已知轴线上一点(x′,y′,z′)以及轴线单位方向向量[l,m,n],即可在原坐标系中求得圆柱中轴线的直线方程。
2.2 模型对称平面提取算法
扭转变形是吊钩形变检测的另一个重要的检测标准,按照国家标准,当扭转变形的角度大于10°时,吊钩应报废。在传统的人工检测方法中,一般使用划线法进行检测,在检测过程中需要把吊钩拆卸下来,然后放在平台上,使用工具进行测量。由大量的检测试验可知,起重机吊钩钩身部分基本不会发生形变。所以在本系统中,通过采集模块得到的完整三维吊钩模型,分割出基本不形变的吊钩钩身以及发生形变的钩尖部分,从这2个部分可以看出是基于某个平面对称的,定义这2个部分的对称面的夹角作为吊钩形变检测的扭转角,作为吊钩形变检测其中的一个标准。以下介绍模型对称平面的提取算法。
在三维模型中,对称性作为其中的一个重要特征,对吊钩的扭转角有着不可或缺的作用。在检测三维模型的平面反射对称性中,有着各种各样的方法,其中Simari等人[14]提出了一种基于迭代重加权最小二乘法的算法。基于这种算法,笔者对其进行了必要的改进,使得可以用之来完成点云模型中的平面对称性的检测。完美对称的三维模型,一般来说都可以用主元分析法来计算其对称面。PCA算法首先需要计算模型数据的协方差矩阵[15-16],接着计算此矩阵的3个特征向量,其中的2个特征向量与此模型的质心唯一确定了该模型的对称面[17]。但是,吊钩并不是完美对称的,对此只用一次PCA法并不能得到准确的对称平面。因此,基于文献[14],提出迭代重加权PCA,以此来检测点云模型的对称平面。但与文献[14]不一样,本文提出了一种新的距离计算方法。

图2 对称面提取算法流程图
以下是迭代重加权PCA的算法过程:首先以每个点元面积为权重,使用重加权PCA计算得到一个近似的平面当做初始对称平面;接着通过一步步的迭代过程不断地调整这个初始对称平面,最终得到一个近于完美的对称面。在每次的迭代过程中,依据一个距离量值来不断地重新计算点元的权重,运用计算得出的权重运行重加权PCA求解得新的近似对称面。对每一个求解得的对称面,使用对称度来定义此对称面的对称程度。若此次对称面的对称度与上一次迭代的对称面的对称度的差值小于一个阈值或者迭代次数已经超过了一定的阈值,则即可终止迭代,此时求解得的对称面即是三维模型的对称面。图2是算法的流程图。
加权PCA。以点云P中的点坐标pi(xi,yi,zi)(i=1,2,…,n)以及对应的权重wi(i=1,2,…,n),以此来求解一个协方差矩阵:
(15)


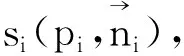
(16)
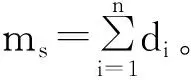
3 吊钩开口度及扭转角的计算
理解上述算法后,本文提出计算起重机吊钩开口度以及扭转角的算法,具体的实现步骤如下:
1)将吊钩放置在扫描仪的视场内,运用电脑控制扫描仪扫描吊钩的各表面,然后融合拼接各个扫描图,并对吊钩点云进行数据精简,提高后期处理的速度,在软件可视化界面中显示完整吊钩点云数据如图3所示。
图3 吊钩点云图
2)运用基于RANSAC的分割算法对吊钩点云数据进行圆柱分割,分割图如图4所示。

图4 圆柱分割图
3)对步骤2中分割出的圆柱进行中轴提取,得到中轴方向向量[l,m,n]以及中轴线方程。
4)在点云模型中,选取距离中轴线小于给定阈值的点,选取在中轴提取时变换坐标系下z值第三小以及第四小的2点的中点为开口度的第一个参照点,如图5所示。
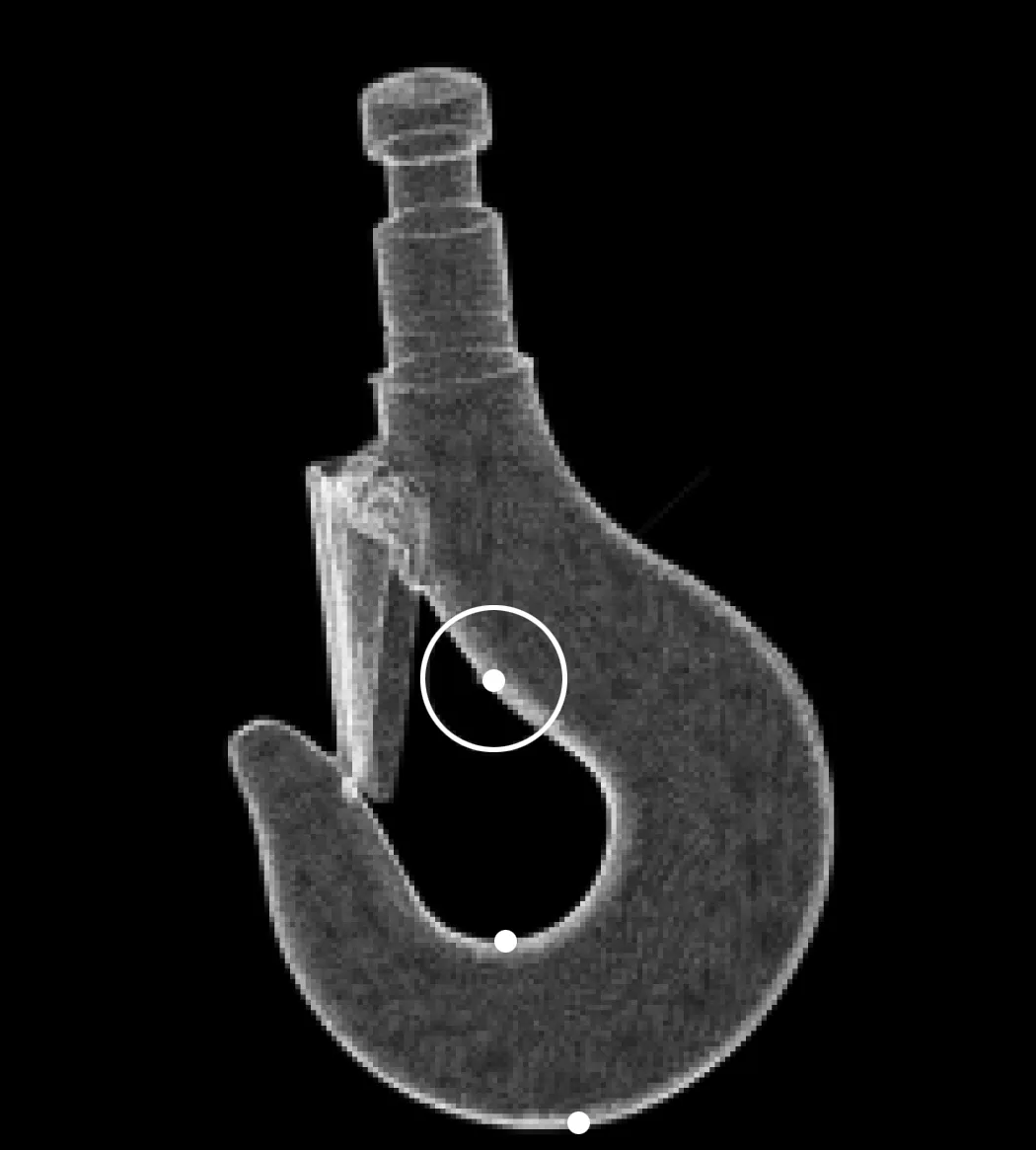
图5 开口度第一个参照点
5)对分割出来的钩身做对称面提取,其重加权PCA计算出的特征向量矩阵为D,D中的前2个列向量与钩身的质心确定的平面即为对称面。钩身如图6所示。

图6 钩身部分
6)对分割出来的钩尖提取对称面,其重加权PCA计算出的特征向量矩阵为C,C中的前2个列向量与钩尖的质心确定的平面即为对称面。钩尖如图7所示。

图7 钩尖部分
7)计算步骤5和步骤6的对称面夹角即为该吊钩的扭转角。
8)以步骤3求得的中轴方向向量[l,m,n]、步骤5求得的特征向量矩阵D的第三个特征向量以及整体点云的质心确定一个平面,平面将吊钩分为2个部分,钩尖所在的部分离此平面最远的点即为开口度的第二个参照点。如图8所示。

图8 开口度的第二个参照点
9)以步骤4得到的第一个参照点与步骤8得到的第二个参照点计算吊钩的开口度。
4 实验结果与分析
在VS2013平台上采用C++语言[18-19]实现本文提出的算法,同时结合点云数据处理库PCL 1.8.0实现[20]。电脑CPU主频为2.3 GHz,内存为16 GB,使用Windows10 64位操作系统。
为了验证本文提出的吊钩形变检测算法的效率以及准确度,与传统的人工检测进行比较,进行吊钩开口度以及扭转角的测量。算法的输入数据来源于DAVID SLS-3结构光3D扫描仪所采集的吊钩数据。
4.1 人工检测
工具:游标卡尺、垂直划线尺、扳手、线、调整垫块、钳子等。
准备工作:检测人员需要用钳子等工具拆卸下起重机吊钩,接着把吊钩放到检测台上,并将吊钩各表面清洗干净。
检查方法:吊钩的扭转变形用划线法测量。把吊钩摆在检测平台上,使用垂直划线尺等工具,找准吊钩的钩身以及钩尖的中心线,然后找出2中心线的交点,钩尖中心线上任意一点向钩身中心线作垂线H,测出垂足到交点的欧氏距离L,最后求解扭转角。
检测时间:工具准备5 min,拆卸吊钩需要大约15 min,人工检测需要大约10 min,把吊钩安装到起重机上需要大约15 min,总共需要大约45 min。
4.2 系统检测
工具:DAVID结构光扫描仪、电脑。
首先,将吊钩放到扫描仪的视场内,同时打开电脑,连接DAVID结构光扫描仪以及电脑,扫描各表面并融合后输出在软件可视化界面上。然后,一键检测输出结果,包含模型分割、中轴提取、对称面提取、开口度和扭转角的计算、结果判定。总共所需时间为8 min,准备吊钩开口度、扭转角的检测的时间大约为5 min,检测和结果判定大约3 min。
如表1所示,与传统的人工检测方法相比,本文实现的吊钩检测方法具有更高的精确性。由于2种方法对开口度选取的标志点不同,无法进行比较,故此只针对扭转角进行比较分析。对于出厂的2T吊钩,出厂的扭转角为0°。人工检测的结果为1.13°,使用本文方法进行检测结果为0.05°。由此可见,本文方法的检测精度更高,同时还具有测量速度快、可追溯性强等优点。
表1 人工和系统检测的对比

检测方式检测时间/min准确度工具检验的追溯性检测指标检测结果人工检测45一般游标卡尺、垂直划线尺等无开口度扭转角8.04%2.38°系统检测8好DAVID结构光扫描仪、电脑强开口度扭转角6.85%1.31°
5 结束语
在起重机械中,吊钩作为一个重要的部件,它的定期检测至关重要。而一种高效、精确、快速的检测算法为其在起重机械中的安全提供了有力的保障。本文提出的吊钩形变检测算法,综合运用点云分割、圆柱中轴提取以及对称面提取这3种算法,对吊钩的开口度以及扭转角进行检测。通过实验结果证明:与传统人工检测相比较,本文算法在检测时间、工具准备、准确度、精度等方面均具有较大的优势,满足实际应用的要求。
