小波分析技术在矿山机械轴承故障检测中的综合应用

陈文占

（长沙矿山研究院有限责任公司，湖南 长沙 410012）

机械滚动轴承是机器运行中的主要工作部件，一旦其受到损害将拉低整个工程的进度，甚至会在挖矿时造成不必要的危险，因此，对于机械运行中机械轴承是否处于良好的运行状态是非常重要的，经过科研人员不断的探索，最终决定采用小波分析技术对矿山机械轴承故障进行检测，其优点在于不仅减少了工作噪音和地表噪音对检测系统的干扰，还提高了检测的可信度和精准性。

1 小波分析技术的工作原理和检测效果

为解决矿山机械轴承故障的分析中存在的问题，人们提出了许多的解决方案，例如采用冲击能量分析法或者冲击脉冲计数法对机械轴承的故障进行分析等。除了前面提及的分析方法之外，还有峰值因子法和峭度因子法，这些分析方法统称为时域分析方法。接着来说一下频域分析方法，其主要分为功率谱分析、倒谱分析、双谱分析和包络解调分析等几种分析方式，在上述几种频域分析方式中，包络解调分析的使用范围是最为广泛的，其因为可以从复杂的调幅振动信号中将轴承故障信息分离出来，所以被应用在大部分地区。

下面简单详细说一下包络解调分析，包络解调分析主要用来分析调幅/调频信号，其主要分为全波整流法、检波滤波法、复调制法、Hilbert变化法等几种方法，这几种方法在实验的过程中得出的结果一般是相同的，但其实现包络解调的方式确大不相同，除此之外，上述几种方法都需要收集共振响应在相对应的窄带滤波过程中，但是在收集的过程中往往会遇到一些困难，因为由于轴承故障所引起的共振频带往往不少，为收集共振响应带来了一定的难度。

而小波变化便可以解决这一问题，因为它的带通滤波的特性可以使经过小波的无用信号被分解掉，从而得到每一频带内振动的情况，进而总结出每一频带内振动信号的变化规律，最后整理出可以反映机械轴承受到冲击而产生的真实的特征频带信号，并用该信号作为检测轴承运行状态的数据。

包络解调分析主要能通过小波变换实现的方法为，先获得解析信号，其过程为将原始故障信号进行Hilbert变换，然后将获得的解析信号做小波变换，使其通过小波变化后在各个尺度上的本质仍为解析信号，然后通过对该变换结果取模的方式得到各个尺度上的包络，然后再用一次傅里叶变换，即可得到小波包络谱，从而完成了小波变换的包络调节分析。进而提高了对机械轴承故障的检测准确性及检测效率。从试验效果看出，包络解调分析方法可以很好的检测出机械轴承故障，有很高的使用价值。

以机械轴承为研究对象，在小波分析技术的支持下，科研人员做了相关的实验，该实验是以探究如何通过小波分析技术来确定机械轴承故障的发生位置为目的，以降低噪音对故障检测为原则进行的，其得出的相关结论也对更好的应用小波分析技术提供了理论上的支持，是对用小波分析技术探测机械轴承故障的肯定和支持。

2 实验过程和结果

首先实验需要在轴承故障试验台上进行，并将实验数据采集系统应用到试验监控系统上，而振动传感器、共振解调仪、电荷放大器三者组成了实验数据采集系统，在实验过程中，采集到的信号先被放大、滤波然后被送进数据采集卡，从而转变数字信息被送入计算器中，因为通过小波变换采集到的数据要在MATLAB条件下才能被处理和编辑，所以我们可以抓住这个特点，运用MATLAB语言编程将时域图和功率谱图绘制出来。

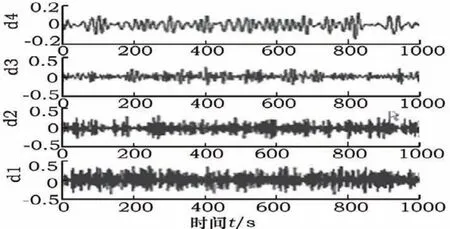
图1 时域图和功率谱图

然后再来说一下轴承故障的模式，在实验运行的过程中，一旦机械轴承存在故障则轴承的其他零件都会对故障点产生周期性的撞击，而其轴承座和支撑结构都会收到冲击力的作用，从而产生一系列的减幅振荡，受轴承几何尺寸、轴的转速和故障点的位置所影响故障特征频率便为减幅振动产生的频率，轴承是否出现故障及出现故障的损失点的位置就可以通过该特征频率检测出来，该轴承的详情见下表1。

表1 轴承特征频率

将上述数据带入频率计算公式得，f1=475Hz,f2=325Hz,振动信号的样品采集是在当振动传感器在减速的箱体上时进行的，其采集频率大致为10.1kHz。先将轴承内环局部剥落设为故障点，此时，内环通过频率f内及其配频为轴承故障的特征频率，通过理论计算可以得出f1=475Hz,然后应用MATLAB小波工具箱里的一维小波，然后将检测的信号通过小波分析技术进行变换，接着重构具有故障特征的信号，然后再用Hilbert变换对拥有故障特征的频率信号进行解调和细化频谱分析，从而检测出轴承中的故障信息成分，从而确定轴承发生故障的位置。通过观察上图，可以看出轴承故障特征最明显的是运用db1小波基检测到的。上面的实验数据可以看出，小波分析技术在轴承故障检测中的效果还是很不错的，但是由于各种限制，实验只研究了大体的测试效果，对于小波分析技术的详细内容并没有进行探索，因此，下面便介绍一下小波分析技术的详细内容和其在轴承故障检测中的应用。

3 轴承故障检测中几种可以用到小波分析技术的情况

小波分析技术之所以可以成为诊断轴承故障的最为广泛且有力的工具之一，是因为其具有很好的分辨率分析能力，而将采集到的信号分解为不同尺度的小波函数之和是小波变换的主要内容，因此小波函数的选择将直接影响到小波的分析效果，而小波变换满足频谱分析方法，所以适用于轴承故障检测领域。

（1）自适应Morlet小波在降噪中发挥的作用。对微弱故障特征频率的采集是现场采集噪音信号和机械设备早起故障信号的关键环节，其将直接影响到对轴承故障的检测，因此，要在采集过程中努力采集到微弱故障特征频率，从而提高检测的准确率，在这种情况下，自适应Morlet小波的微弱故障特征提取法是最佳的选择，其大致过程为:首先用修正Shannon熵的方法对Morlet小波的中心频率和宽带参数进行优化，从而获得最符合故障特征成分的自适应Morlet小波。然后在运用改进过是矩阵构造法将小波变换系数构造成矩阵的形式，并解出奇异值，在对其进行分解，其表达式为A=UV∧T=∑kUiVi∧T，其中矩阵A的秩用字母k表示，矩阵AA∧T和A∧TA的第i个特征量用Ui和Vi表示，因为每一个小波都有一个相对应的尺度a，因此便可以解出一个周期性指数与相对应尺度的函数关系式，即为尺度周期性指数关系式:Ψ(a)=(k2-k1)/k1,将SPE谱的最大值求出，便可得到最佳的小波变换尺度，最后，在对信号进行过滤除杂，从而得到真实的故障特征信息。

（2）Laplace小波分析技术在过滤波中的应用。在Laplace小波基函数库的基础上建立循环Laplace小波相关过滤法，因为Laplace小波相关过滤法可以辨识对故障进行冲击收到的响应参数成分，并依据其辨识到的特征参数，构造循环Laplace小波函数，并对响应信号中的循环周期进行寻换冲击，然后用相关滤波监测系统进行检测，下面说一下周期循环信号中的特征参数和循环周期如何用循环Laplace小波相关滤波法识别出来，首先，通过上述冲击故障接收频率的方法建立起Laplace小波基函数库，然后再辨识响应冲击波形的特征参数，通过Laplace小波相关过滤法即可实现，最后利用寻循环Laplace小波滤波法的定义，将冲击响应成分特征参数辨识结果构造成循环Laplace小波函数，并利用相关滤波函数，尽可能的确定循环周期为多少。

（3）小波相关排列熵在提取特征频率上的应用。当机械轴承开始出现故障时，检测仪器接收到的频率是微弱的，同时在噪音的影响下，很难直接提取出微弱的故障频率，即使通过小波分解技术也不容易。小波相关滤波法不仅可以有效的降低噪音，还不会损失分辨率。所以，WTCE可以帮助相关人员提取信号出现故障的具体表现，从而找到信躁相对来说比较高的各层重构信号。由于上述的一些相关的情况，可以对小波相关滤波处理的结果进行相关的分析。从而可以得出各阶段信号的排列熵复杂度，并且因此以了解知机械系统的工作状态。

4 结语

从上述所有实验可以知道，在收集故障特征频率时，运用小波分析技术不仅可以检测出是否发生了故障，还可以检测出故障发生的部位，从而大大减少了停工的时间，促进了施工进度，同时小波分析技术还避免了建立机械轴承振动信号的数学模型的麻烦，同时其还具有很多优点，例如，特征参量比较少、故障特征突出等，非常适合应用于矿山机械轴承故障的检测。