中美标准地震反应谱对比分析
2018-08-03李俊义吴灵宇胡亚东
李俊义,吴灵宇,胡亚东
2015年,天津水泥工业设计研究院有限公司签署了印尼某水泥生产线建设合同,业主要新建一条完整的5 000t/d水泥生产线。根据合同要求,烧成窑尾、窑中、生料库、熟料库、水泥库、辊磨基础按美国标准设计,其余车间按中国标准设计。因此,熟悉中国和美国规范地震反应谱的取值,对合同的执行有着非常重要的作用。
1 中美规范抗震设防目标
中国建筑抗震设计规范GB 50011-2010以三个水准为抗震设防目标,即“小震不坏,中震可修,大震不倒”。根据国内统计分析,以50年内超越概率为63%的地震烈度为第一水准烈度,即多遇地震(小震);以50年内超越概率为10%的地震烈度作为第二水准烈度,即设防烈度(中震);以50年内超越概率为2%~3%的地震烈度作为第三水准烈度,称为罕遇地震(大震)。当遭遇第一水准烈度时,建筑处于正常使用状态,从抗震角度分析结构为弹性体系,采用弹性反应谱进行弹性分析;当遭遇第二水准烈度时,结构进入非弹性阶段,但非弹性变形或结构体系的损坏控制在可修复的范围;当遭遇第三水准烈度时,结构有较大的非弹性变形,但控制在规定的范围内,以免倒塌。
中国规范要求采用二阶段设计实现上述三个水准的设防目标。通过第一阶段设计-承载力验算,取第一水准的地震动参数,计算结构的弹性地震作用标准值和相应的地震作用效应,使结构既满足了在第一水准下具有必要的承载力可靠度,又满足了第二水准的损坏可修的目标。第二阶段设计是弹塑性变形验算。对于大多数结构,只需进行第一阶段设计,通过概念设计和构造措施,使结构满足第三水准的要求。
美国规范ASCE 7-10 Minimum Design Loads for Buildings and Other Structures是以50年内超越概率2%的地震作用作为最大考虑地震作用,在实际计算中乘以相应的修正系数。
2 场地技术条件
通过解读项目地勘报告,场地土的剪切波速为183~366m/s,根据ASCE 7-10表格20.3-1场地土的判定标准,场地类别为D类(坚硬场地土,剪切波速位于182.88~365.76m/s之间)。
根据地勘报告及印尼当地官方地震加速度信息:场地短周期反应谱加速度SS为0.52(g),1s反应谱加速度S1为0.33(g),场地调整系数Fa=1.31,Fv=1.81。
根据ASCE 7-10第11.4.3章节可计算出MC⁃ER-场地地震最大影响系数:
SMS=Fa×SS=1.31× 0.52=0.681 SM1=Fv×S1=1.81× 0.33=0.597
根据ASCE 7-10第11.4.4章节可计算出设计水平地震影响系数:
SDS=2/3× SMS=2/3× 0.681=0.454 SD1=2/3× SM1=2/3× 0.597=0.398
根据表1、2(国标GB 50011-2010第四章表4.1.3、表4.1.6),场地土的类型应为中软土/中硬土,同时考虑覆土深度,判定场地类别为Ⅱ类,第二组。
根据表3(国标GB 50011-2010第五章表5.1.4-2),场地特征周期为0.40s。
3 不同结构形式的中美标反应谱
3.1 设计反应谱加速度
根据图1(ASCE 7-10,第11.4.1章节,图14.1-1),地震反应谱如下:

表1 土的类型划分和剪切波速范围*
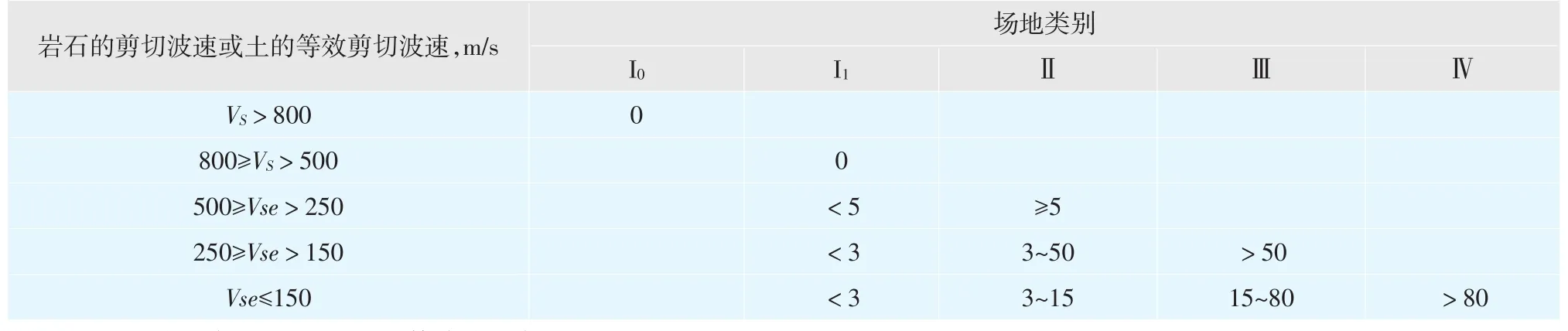
表2 各类建筑场地的覆盖层厚度*,m

表3 特征周期值,s

图1 设计反应谱加速度
(1)周期<T0,设计反应谱加速度Sa应按式(1)(ASCE 7-10,公式11.4-5)计算:
Sa=SDS(0.4+0.6T/T0)(1)
(2)周期≥T0,且<TS,设计反应谱加速度Sa:
Sa=SDS(2)
(3)周期>TS,且<TL,设计反应谱加速度Sa应按式(3)(ASCE 7-10,公式11.4-6)计算:
Sa=SD1/T (3)
(4)周期>TL,设计反应谱加速度Sa应按式(4)(ASCE 7-10,公式11.4-7)计算:
式中:
SDS——短周期设计反应谱加速度系数
SD1——1s周期设计反应谱加速度系数
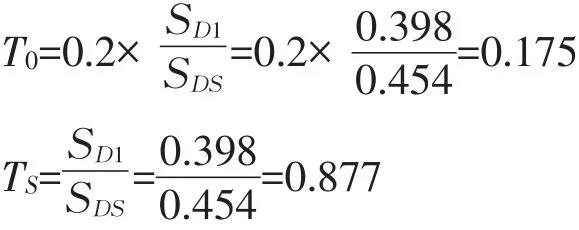
T——建筑物的特征周期TL——长转换周期,美国地区处于4s~16s之间;为便于对比,参照中国规范,取值6s
3.2 中美标准反应谱计算实例
本水泥厂项目采用美标设计的车间结构形式主要分为三种:中心支撑钢框架(烧成窑尾)、钢筋混凝土筒仓(各种储库)和大块式设备基础(窑中,辊磨基础),本文着重从中心支撑钢框架和混凝土筒仓两方面进行中美标准反应谱的对比分析。
3.2.1 中心支撑钢框架反应谱计算实例(Ra=3.25)
根据美标ASCE 7-10,水泥工厂的建筑设计风险级别可定义为Ⅱ级,结构的重要性系数可取1.0。根据美标ASCE 7-10第12.2-1章节,中心支撑框架反应谱加速度调整系数Ra可取3.25。为计算需要,同时考虑更直观的对比,将结构重要性系数和反应谱加速度调整系数融合到反应谱曲线中。
中心支撑钢框架美标修正后的反应谱参数如下:
SDS=0.454/(Ra/Ie)=0.140 SD1=0.398/(Ra/Ie)=0.122
Ie为地震力影响系数,此处取1.0。
根据上述参数可绘制出美标反应谱,见图2。参考美标峰值加速度信息,国标反应谱按8度,0.20g考虑,峰值加速度为0.16(阻尼比ζ=0.05)。根据图3(GB 50011-2010,第5.1.5章节),中国标准的地震反应谱如下:
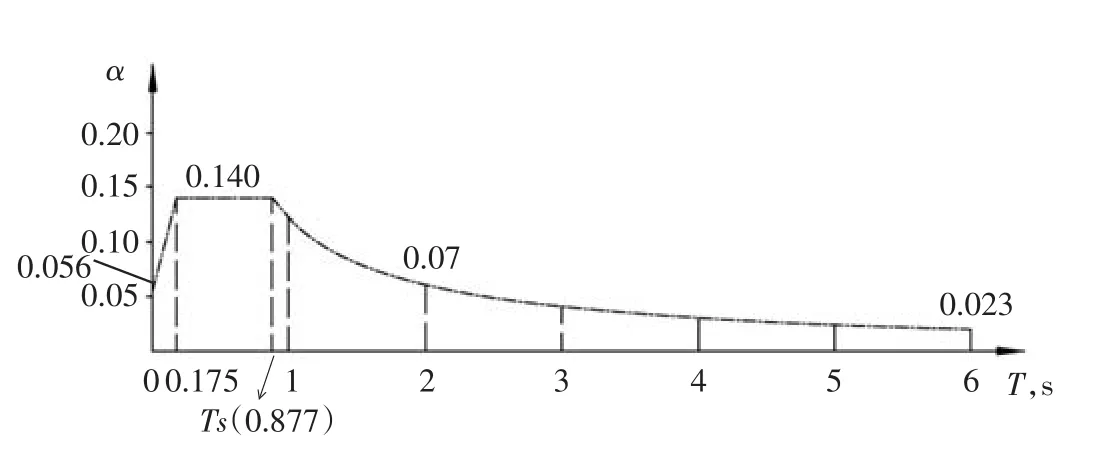
图2 美标反应谱曲线(Ra=3.25)


图3 地震影响系数曲线
当周期位于Tg~5Tg时:
α=(Tg/T)γη2αmax(5)当周期位于5Tg~6s时:
α=[η20.2γ-η1(T-5Tg)]αmax(6)式中:
α——地震影响系数
αmax——地震影响系数最大值
η1——直线下降段的下降斜率调整系数
γ——衰减指数
Tg——特征周期
η2——阻尼调整系数
T——结构自振周期其中:(1)曲线下降段的衰减指数γ应按式(7)确定:γ=0.9+(0.05-ζ)/(0.3+6ζ)(7)式中:
γ——曲线下降段的衰减指数
ζ——阻尼比
(2)直线下降段的下降斜率调整系数η1应按式(8)确定:
η1=0.02+(0.05-ζ)/(4+32ζ)(8)式中:
η1——直线下降段的下降斜率调整系数,<0时取0
(3)阻尼调整系数η2应按式(9)确定:
η2=1+(0.05-ζ)/(0.08+1.6ζ)(9)
式中:
η2——阻尼调整系数,当<0.55时,应取0.55
本车间高度为90.45m,结构阻尼比ζ按0.03考虑,可相应绘制出国标对应的反应谱,详见图4。
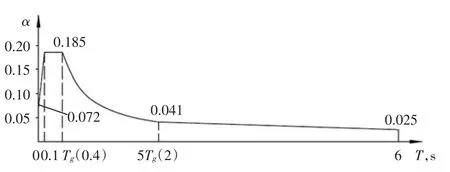
图4 国标反应谱曲线(阻尼比0.03)
通过对比图2和图4,国标反应谱峰值高于美标,但国标反应谱加速度随周期衰减较快,为了更直观对比其关系,我们将两个反应谱叠加在一起,详见图5。
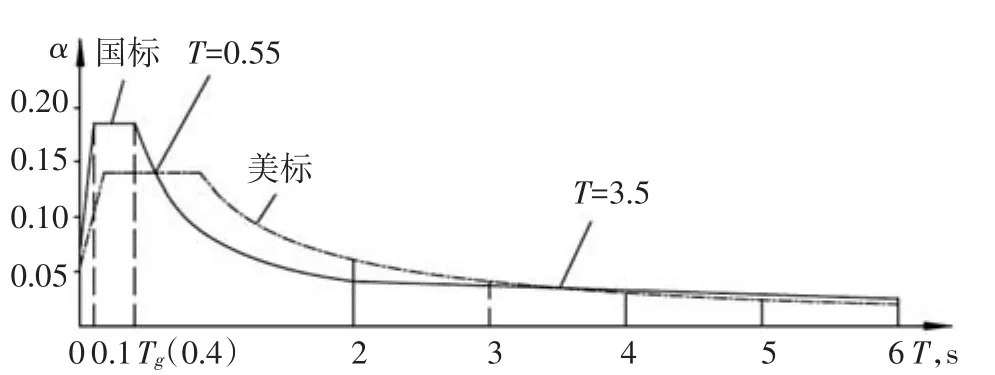
图5 反应谱对比(阻尼比0.03,?Ra=3.25)
从图5可明显看出,在周期0~0.55s之间,国标加速度值明显高于美标;但从0.55s~3.5s,由于国标衰减较快,在此范围内美标的加速度值要高于国标;从3.5s~6s,国标加速度稍高于美标,但相差不大,两条曲线基本重合。
从分析结果看,本车间第一周期约为2.5s,对应美标加速度值为0.049(g),国标加速度值为0.039(g),美标加速度较国标加速度高出约25.6%。3.2.2 钢筋混凝土筒仓反应谱计算实例(Ra=3)
根据美标ASCE 7-10第15.4-2章节,钢筋混凝土筒仓的反应谱加速度调整系数Ra可取3。
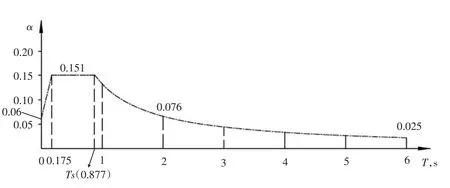
图6 美标反应图谱曲线(Ra=3)

图7 国标反应谱曲线(阻尼比0.05)
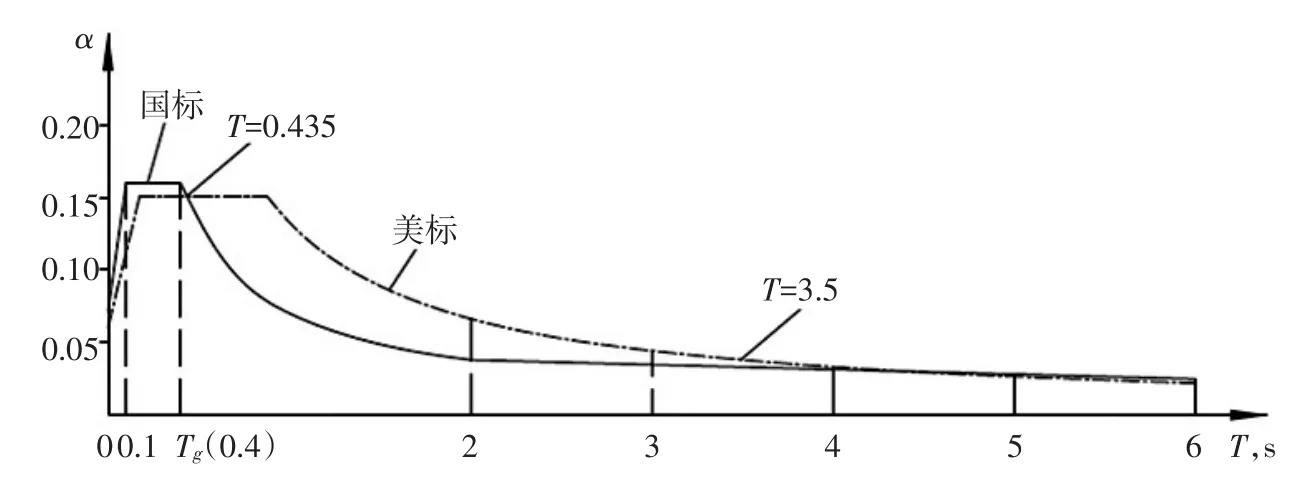
图8 反应谱对比(阻尼比0.05,Ra=3)
则美标修正后的反应谱参数如下:
SDS=0.454/(Ra/Ie)=0.151
SD1=0.398/(Ra/Ie)=0.133
根据上述参数可绘制出美标反应谱,见图6。
以生料库车间为例,筒仓内径为20m,高度为63.5m,结构阻尼比ζ按0.05考虑,可相应绘制出国标对应的反应谱,详见图7。
通过对比国标和美标反应谱信息发现,国标反应谱峰值高于美标,但国标反应谱加速度随周期衰减较快。同样,我们将两个反应谱叠加在一起,见图8。
从图8可明显看出,在周期0~0.435s之间,国标加速度值明显高于美标;但从0.435~3.5s,由于国标衰减较快,在此范围内美标的加速度值要高于国标;从3.5~6s,国标加速度基本等同于美标,两条曲线基本重合。
从分析结果看,生料库空仓状态下第一周期约为0.473s,对应美标加速度值为 0.151(g),国标加速度值为 0.141(g),美标加速度较国标高出7.1%,两者相差不大;生料库满仓状态下,第一周期为0.60s,对应美标加速度值为0.151(g),国标加速度值为0.114(g),美标加速度较国标加速度高出约32.5%。
通过以上计算实例可以看出,同一结构的不同状态,由于自震周期的区别,水平加速度的差别非常大。
4 结语
通过分析相应的中美标地震反应谱,我们对采用中美标准计算的结果差异有了一个初步的认识。国标反应谱峰值加速度较大,但随着周期衰减较快;美标反应谱峰值加速度较国标偏小,但随周期衰减较慢。通过本文的两个计算实例可以看出:在0~0.5s,国标的反应谱加速度较大;在0.5~3.5s,美标的反应谱加速度较大;3.5s以上,美标和国标的反应谱加速度差异不大,基本相同。但需注意,对不同的场地,因为特征周期的不同,曲线规律会有一定的区别。
