基于深度学习的数据特征的提取与预测研究

杨天瑞，孙伟东

（沈阳航空航天大学计算机学院，沈阳 110000）

随着科学技术的不断发展，我国进入到大数据时代，在此时代背景下数据预测与应用成为数据技术开发的重要部分。现阶段，阿里集团、腾讯、谷歌等都陆续认识到大数据的重要作用，突出体现便是“双十一”购物节的成功运营，使当天的销售额能够达到前十一个月的20倍以上，这与数据特征提取与预测之间有着十分重要的促进作用。

1 基于深度学习的数据特征提取

社区结构主要是社区内部各要素之间形成的相对稳定的关系，属于由各个要素的共同作用下组成的有机系统。在对社团演化预测过程中，考虑到社团演化中的合并问题，因此在预测模型中通常提取社团内部的特征，包括规模、内度、内外部连边的比值等等，这些特征只是单纯的能够体现某个社团，因此需要对社团之间的共性特征进行提取，才能够对多个社团合并事件进行预测。

通过现有的研究表明，社团的性质能够通过规模和内外连边比值体现出来，所谓的规模也就是节点数量，规模越小的社团发生合并的几率将越高，而社会的数量只能体现其规模，却无法表现其稀疏程度。因此，需要加入内外连边比值特征，该特征主要是指社团外部与内部连边数量的比值，且比值与社团合并可能性之间呈现正比例关系，如若内部连边与外部连边相比，增长速度较低，则会增加合并的几率，因此可以通过对内外连边比值测试的方式，对社团的演化趋势进行预测[1]。

假设G=（V，E）属于无权无向网络，具有N个顶点，且顶点集合V的取值范围为V1到VN，顶点与集合二者的连边用E来表示。同时，该网络的邻接矩阵属于一个角对称矩阵，将其表示为：

式中，i与j均表示顶点；aij表示两个顶点间的连边，其数值为1；当aij的数值为0时则表示两个顶点连边之间不存在连边，这时i的取值范围在0到N之间，i的度数表示为：

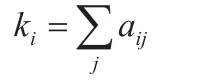
Ci与 Cj属于两个随机社团，二者之间的连接度为 Bd（Ci，Cj），能够与社团之间相连的一阶差值为△Bd（Ci，Cj），二阶差值为△△Bd（Ci，Cj），并且计算方式分别为：

一阶差值 ：△ Bd（Ci，Cj）=Bd（Ci，Cj）t=to-Bd（Ci，Cj）t=to-△t

二阶差值：△△ Bd（Ci，Cj）= △ Bd（Ci，Cj）t=to-△ Bd（Ci，

式中，t0代表的是时间段；△t0代表的是时间步长。

综上可知，在社团结构中共计需要提取出四个特征数据，分别为 Ni社团大小、连接度 Bd（Ci，Cj），以及一阶差值为△ Bd（Ci，Cj）、二阶差值为△△ Bd（Ci，Cj）。

2 社团合并预测模型的建立

2.1 深度学习模型的构建

DBN属于一个概率生成模型，将样本标签数据当中的特征值有效的提取出来，利用该模型获取到社团特征以后进行预测分析。通常波尔兹曼机的输入范围为0-1之间，但是在社会合并预测中，特征向量具有连续性，因此可以将RBM中的实值特征转变为二进制变量。在低维空间中，将样本数据转变为高纬度向量，然后输入到向量训练层当中，由此完成在深度学习基础上的社团合并预测模型的建立[2]。

2.2 模型的训练算法

由于以往采用的BP算法中存在较大的误差信号，很可能出现“梯度扩散”现象，影响训练效果。因此，本文采用贪婪逐层算法的方式，对整个网络进行训练。贪婪逐层算法是将样本数据看作成输入量，对首个RBM进行训练，并在此基础上对第二个RBM进行输入，从而训练出第二个，以此类推，直至所有深度学习网络全部被训练完成。在算法流程方面，主要内容如下。

（1）利用CD算法对特征向量X进行训练，从而得出第一个RBM。

（2）利用上一个RBM作为向量，输出下一个RBM。

（3）重复第二步，直至使所有RBM均完成训练。

（4）通过最后一层得出RBM输出向量，将输出向量看做成回归预测层输入向量，并且对参数进行初始化处理。

（5）利用带标签的数据和BP算法，通过从上到下的方式，对整个预测模型参数进行细微的调整，进而获取预测模型参数。

利用上述贪婪逐层算法对各个RBM进行训练以后，便能够建立DBM预测模型，进而通过数据集的方式对社团的合并进行分析和预测。

3 结束语

综上所述，本文针对大数据时代下的数据预测进行分析，在深度学习背景下，在RBM基础上建立了结构模型，对智能家居发展趋势进行预测，并且提出了社团检测方法，最后在时间序列数据预测的基础上，对复杂网络的社团演化进行预测，这对于智能家居行业的实际工作来说具有较大的应用价值与现实意义。