CT系统参数标定与图像重建数据分析

徐 琳，赵晓卓

（河北农业大学，保定 071000）

1 CT成像概述

CT，即电子计算机断层扫描，利用平行入射且垂直于探测器表面的X射线通过发射-探测系统进行断面扫描，发射器和探测器固定位置不变，整个系统绕某固定的旋转中心逆时针旋转180次。其广泛可用于医学检查、工业检测等方面。

确定CT系统参数和成像问题，一般是利用样品对射线的吸收特性来进行断层成像，对每一个X射线方向，在具有多个等距单元的探测器上测量经位置固定不动的二维待检测介质，处理后得到180组接受信息。而系统安装往往存在误差，影响成像质量，所以我们要对其进行参数标定。影响图像质量的参数有空间分辨力、密度分辨力、噪声、层厚与层距、场均匀性等等。我们可以借助已知结构的样品标定CT系统的参数，之后对未知结构的样品进行成像。

2 参数标定步骤

Ct参数的标定大概分为三个步骤，分别是：

（1）计算探测器单元之间的距离。

（2）计算X射线的180个方向。

（3）计算旋转中心的位置。

3 图像重建原理

3.1 重建原理概述

我们通过查找资料在均匀物体中x射线是按指数衰减的。在不同物体中x射线的衰减函数的系数不同，设穿过的系数为u1、u2u3……un。

假设发射出的射线强度为t0，那么接收到的x射线强度为t，此式可转化为

由于接收强度较小，所以一般将ui进行一定比例的放大，得到CT值，

将CT值用灰度图像表示出来，即为CT图像

3.2 图像重建原理

在旋转中心O处建立坐标系，CT系统逆时针旋转。假定CT系统固定不动，建立xoy坐标系，相对于CT系统正方形托盘顺时针旋转，以O为原点建立sot坐标系。

（1）坐标系的建立

在旋转中心o处建立xoy坐标系和sot坐标系。其中探测器在s轴上。xoy坐标系固定，sot坐标系绕o点旋转。

（2）由图形得到投影值

（3）由投影对图形进行重建

由中心切片定理[1]：二维物体函数f（x，y）的线积分投影数据p（s）的一维傅里叶变换p（w）等于二维物体函数f（x，y）的傅里叶变换F（wx，wy）沿与探测器平行方向过原点的一个一维切片即对pθ（s）进行一维傅里叶变换的结果与原图像进行二维傅里叶变换的结果相同。

所以，将pθ（s）进行一维傅里叶变换之后，再对其进行二维傅里叶反变换，即可得到原图像f（x，y）

其中R为r的频域分量，（u，v）为（x，y的频域分量），u=R cos θ、v=R sin θ。

3.3 Radon变换与Radon反变换

（1）Radon变换

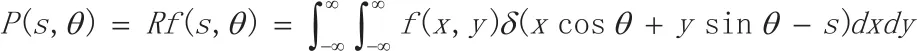
（2）Radon逆变换

由投影值得到原图形，即将Radon变换公式反演。公式：

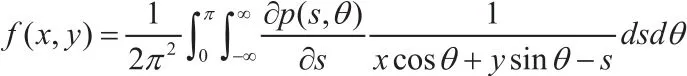
可以直接利用Radon逆变换公式反投影：将p（s，θ）按公式直接投影到原来的像素点上。

但是此方法会导致投影不清晰。所以我们决定加入S-L滤波函数来进行求解。

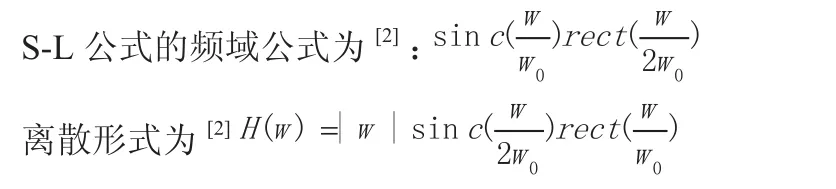
（3）模型求解

对于该公式，在计算机中我们需要用求和代替积分，用差分代替微分。

所以Radon逆变换的公式为：

依此方法可对图像进行重建。

4 结束语

由于CT系统本身安装时往往存在误差，会导致投影数据的测量发生错误。而本文提出的Radon变换原理和中心切片定理，通过这种算法可以得到较为准确的CT系统的成像。建立不同的模型，尽可能减小机械误差造成的影响，使得最终结果更精确。S-L反投影图像要比直接投影图像清晰。