巧用“三变” 解三角问题

河北易县中学 边红霞

三角函数是高中的重要内容，也是高考的必考内容。无论是化简、求值、证明，还是研究三角函数的性质，都离不开三角恒等变形，如何选用公式成为解决问题的瓶颈，熟练掌握三角公式是基础，灵活运用是关键。解决三角问题的方法灵活多样，然而也体现出一定的规律性。对式子结构进行全面分析，合理选择一个突破口，或是从角度入手 ，或是从三角函数的名称考虑，或改变式子的结构，通过变角、变名、变式，简称“三变”，即可顺利解决三角问题。

对三角问题，因公式繁多，思考的角度不同，选择公式的顺序不同，会出现不同的解题思路，下面这道题就是一个典型的例子，通过它，我们会发现解决三角问题的一般规律。

分析：解决这类问题，一般从三方面考虑：观察角、名称、式子的结构。此函数式是一个分式，含有二倍角，有两个三角函数的名称，考虑利用公式对函数式进行化简。

一、变角

在三角恒等变形中，首先要从角、名称、式子的结构进行全面分析，当式子中角不统一时，可以“以角”为突破口，充分利用角的变换，进行有目地的变形，使得角达到统一。经常使用的公式有二倍角公式、诱导公式、两角和与差等。

思路1：我们先从“角”考虑，用二倍角公式，角度减半，方次升高，会产生因式，消去公因式，然后统一名称，转化为一个角的一个三角函数。

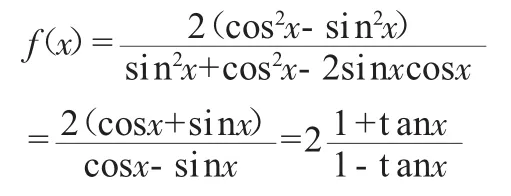
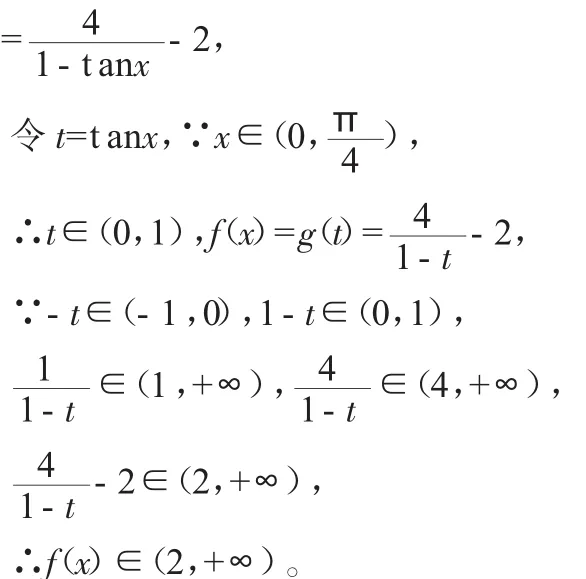
思路2：由思路1变形得到 ，分析“角度”，为使角统一，分子分母分别用辅助角公式，这样形成一个角的一个三角函数。

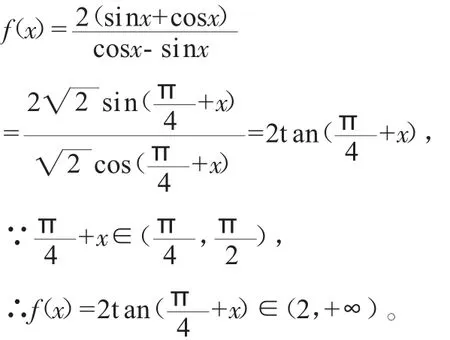
二、变式

当题目中式子的结构比较复杂，比如有分式、方次高等，可以通过恒等变形，改变式子的结构，化分式变为整式、由高次降为低次，目的是使复杂的结构变得简单。

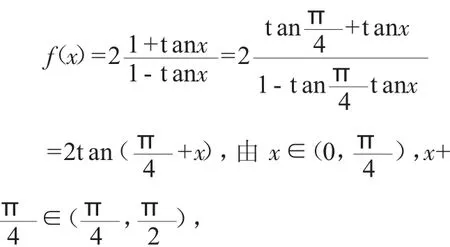
∴ （fx）∈（2，+∞）。

思路4：从“式子”的结构分析，如果分母变为单项式，可以有约分的机会，于是，从角入手，使用诱导公式，再用二倍角公式，角度减半，方次升高，统一为一个角的一个三角函数。

三、变名

如果在式子中存在多种三角函数，要利用公式统一名称，常用的有诱导公式、同名三角函数间的基本关系式、辅助角公式等，但在统一名称时也是从角度入手。

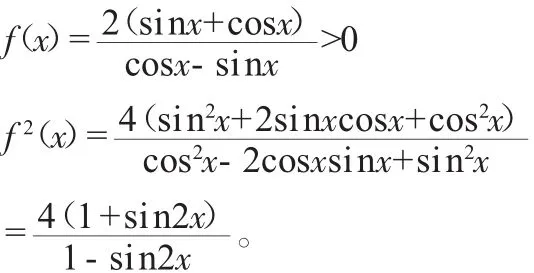
令 t=sin2x∈（0，1），

从以上分析可以看出，恒等变形的基本思路是进行“三变”，即“变角”“变名”“变式”，三变是进行三角恒等变形的桥梁，是解决三角问题的灵魂，任何变形都是围绕这三方面进行的。

通过以上题目发现，“三变”之间不是割裂的，而是相互交融，在进行一种变换的同时，伴随着其他变换的发生。即在进行式子结构的变化中，融入了角的变换，同时名称也得到了统一，只是先选择一个突破点而已。一般是先看角，从此出发，进行综合考虑，兼顾三角函数的名称，简化式子的结构，便可顺利解决三角问题。