基于高斯模型的新场气田输气管道泄漏模拟研究

廖 毅，于 川，孙昊茹

(中国石化西南油气分公司采气一厂，四川德阳 618000)

新场气田地处四川盆地西部，上世纪90年代获得产量突破，由于建产时间早，管辖井数多，地下输气管线层层叠叠，错综复杂，存在管线老化、腐蚀、机械损伤与城镇建设侵扰等因素，导致长输天然气管道泄漏与爆管几率增加，可能引起火灾甚至爆炸等严重后果[1]。因此，有效预测长输天然气管道泄漏过程，计算不同泄漏时刻天然气燃爆极限距离，对新场气田管道安全评价、事故应急预案制定具有重要意义。

针对天然气泄漏扩散预测已经有了很多研究。理论模型主要有高斯模型、Sutton模型、BM模型与FEM3模型[2]。高斯模型在20世纪50年代提出，虽然预测精度不高，但实验数据丰富，计算简洁，广泛应用于污染物扩散领域[3];Sutton模型从湍流扩散统计理论出发，但模拟可燃气体泄漏时误差较大;BM模型是基于大量实验数据获得的经验模型，反映重气泄漏规律;FEM3模型为三维有限元模型，模拟效果较好，但模型复杂，计算量大，对设备要求高[4]。

新场气田的开发已经步入了中后期，管线压力低。高斯模型方法成熟，适用于低动量泄漏与扩散过程的模拟[5]，因此，笔者采用高斯烟团模型，并进行了修正，模拟了天然气管道泄漏扩散过程，并进行了敏感性分析，最后就新场气田长输气管道泄漏实例进行了模拟计算。

1 模型建立

1.1 天然气泄漏速度计算

天然气管道泄漏形式包括孔口泄漏、裂缝泄漏与全管径断裂，其中前两种是主要泄漏形式。在实际生产过程中通常发生的泄漏事故为小孔径泄漏。为了方便计算，通常将孔口与裂缝等非规则形状依照面积守恒等效为圆形，并以此为基础进行计算。小孔泄漏可以看作绝热过程，基于伯努利方程与绝热方程，可以计算其泄漏速度[6]:

式中:q——体积流量，m3/s;

φ——流速系数，一般取值为0.97～0.98;

D——泄漏孔口直径，m;

P1——天然气管道内压力，Pa;

P0——管道外环境压力，Pa，通常取大气压;

R——气体常数，其值为8.314 J/(mol·K);

T——管道内气体温度，K;

k——绝热指数，针对天然气，k通常取1.28[7]。

CD——流量系数，也被称为泄漏系数，其取值范围见表 1[8]。

对式(1)进行整理，可得:

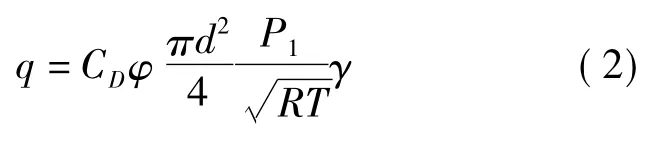
式中:γ——泄漏速度系数，该系数取决于孔口流动速度是否处于音速状态，通常通过临界压力比(CPR)进行判定。CPR表达如下:

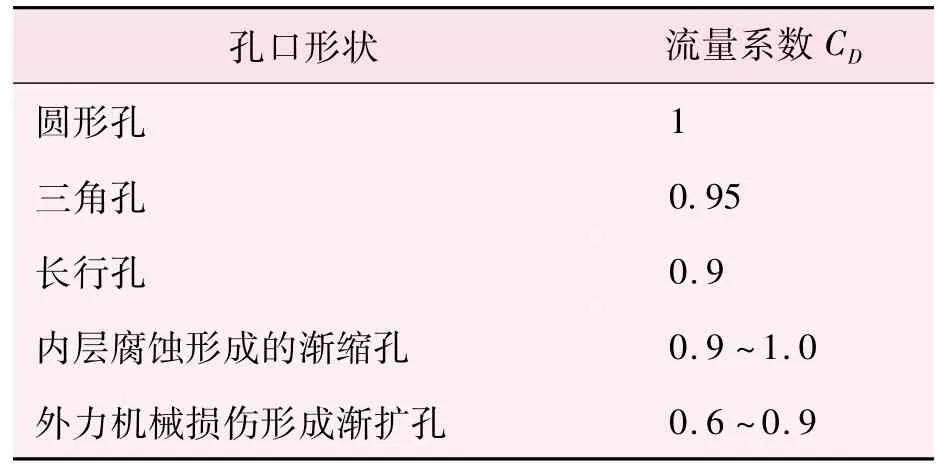
表1 不同形状泄漏孔流量系数CD取值

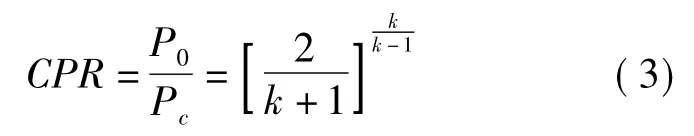
式中:Pc——为气体速度为音速时对应的临界压力，Pa。对于天然气，其临界压力为1.82×105Pa[7]。因此，气体泄漏系数γ可表示为:

在管道孔口泄漏过程中，管内压力会不断降低，泄漏速度不断下降。何沫[9]对输气管道泄漏速率衰减因子λ进行了详尽研究，研究表明:泄漏速率衰减因子λ不受管道压力变化影响，而随管径的减小而减小。给出λ的经验公式:若为了保守的满足安全管理要求，可将泄漏速率衰减因子取为0.33。

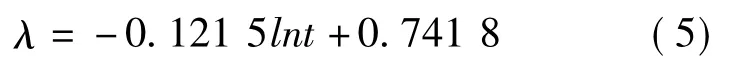
因此，不同时刻天然气输气管道的泄漏速度可以表示为:

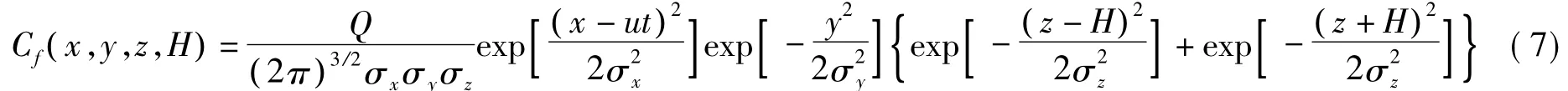
式中:Cf(x，y，z，H)——气体在坐标 (x，y，z，H)处的浓度，mg/m3;

Q——泄漏量，m3;

σx，σy，σz——气体在 x，y，z 方向的扩散系数，m，通常取σx=σy。

针对地面天然气管线短时间泄漏，只需考虑泄漏的天然气在地面的浓度，因此，可以将式(7)简化为[4]:

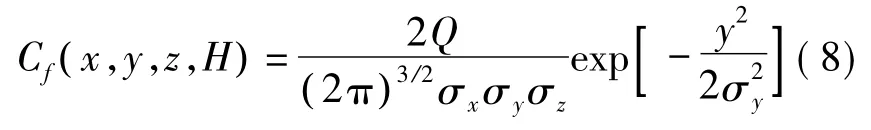
式中:qa——气体真实泄漏速度。

结合式(2)～(6)，可以计算获得不同压力、不同孔口的输气管道在不同时刻的天然气泄漏速度。

1.2 天然气扩散浓度分布

高斯模型包括高斯烟羽模型与高斯烟团模型。高斯烟羽模型适用于气源稳定、连续、恒速的释放扩散，高斯烟团模型适用于气源瞬时扩散。天然气输气管线泄漏发生后，短时间内泄漏出大量天然气，更加适合于高斯烟团模型。高斯烟团模型的气体扩散浓度分布表示如下:

气体扩散系数的确定是高斯模型求解的关键，目前尚无确定的理论模型可以求取气体扩散参数，通常采用经验公式进行描述。Pasquill[10]提出了大气稳定度理论，按照风速、日照、阴云等天气情况将环境条件分为6类，具体见表2。

Briggs基于大气稳定度理论，通过插值获得了不同大气稳定度下天然气扩散系数表达式，具体计算公式见参考文献[10]。廖倩雯[4]提出扩散系数同样受到地面粗糙度的影响，应该基于地面粗糙度与大气稳定度对扩散系数计算进行修正，并给出了修正公式，表示如下:

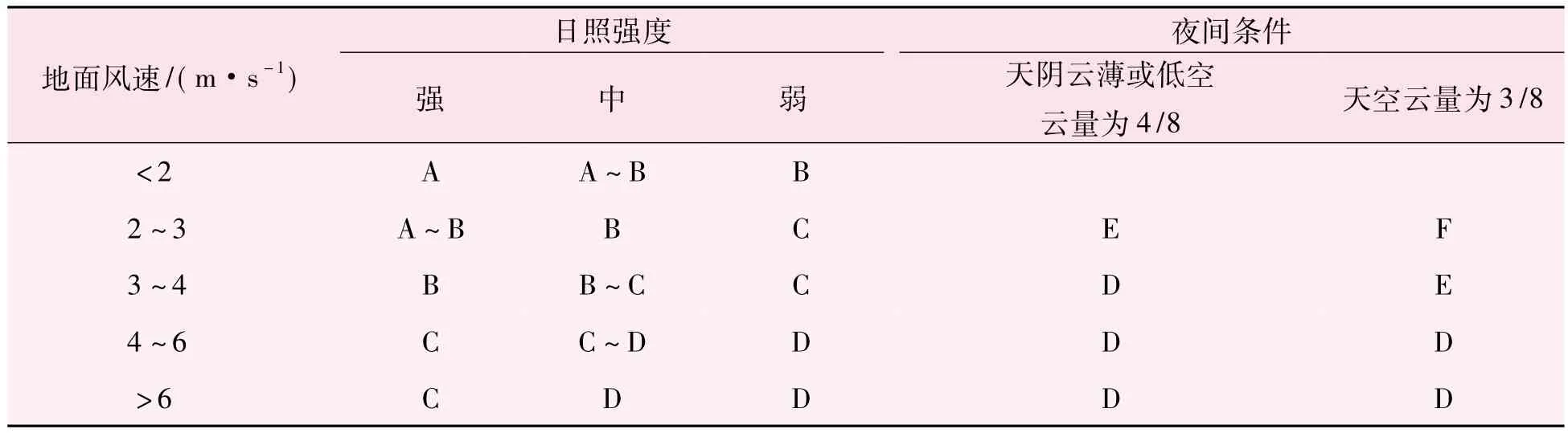
表2 大气稳定度分类

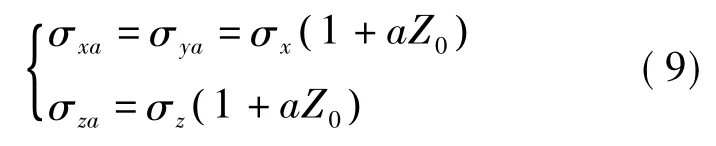
式中:σxa，σya，σza——修正后的气体扩散系数，m;

a——不同大气稳定度下的修正系数，取值具体见表3;

Z0——地面粗糙度，取值具体见表4。

表4 地面粗糙度取值[4]

将修正系数a与Z0带入式(9)，计算不同环境条件下的扩散系数，结合式(8)，即可求取不同质量烟团的扩散浓度。

将天然气泄漏过程等效为多个烟团连续释放，每个烟团瞬时释放，通过式(6)计算获得每个时间节点的天然气泄漏速度，继而通过式(8)获得每个烟团在地面的质量浓度，最后将不同时间释放的烟团的浓度进行叠加，即可获得不同时刻天然气泄漏的质量浓度。

2 敏感因素分析

天然气的爆炸极限为5% ～15%，因此当天然气的质量浓度达到40 000 mg/m3时，就可能存在爆炸风险。通过对建立模型进行求解，模拟了不同条件下天然气浓度分布，并对其进行了敏感性因素分析。

若无特别说明，模型参数设定如下:管道压力为3 MPa，环境温度为23℃，泄漏孔径为50 mm，大气稳定度为C，孔口泄漏系数为1，地面粗糙度为0.5，天然气绝热系数为1.28。

2.1 管道压力影响

管道压力决定着天然气泄漏速度，从而影响着天然气燃爆区域。其他条件不变，分别模拟了管道压力为0.5，1，2 MPa时天然气的浓度分布，见图1。黄色区域为天然气浓度大于40 000 mg/m3的区域，即为燃爆可能发生区域。随着管道压力的升高，管道泄漏处的燃爆区域主要向下风向扩展，在垂直于下风向的方向扩展不大。天然气泄漏在下风方向的浓度最高，出现燃爆可能性最大。为了保守估计安全范围，应取下风向的燃爆极限距离为安全距离。不同管道压力条件下的下风向燃爆极限距离如图2所示，下风向燃爆极限距离随着管道压力增高而增加，其上升趋势出现先迅速上升后逐渐平缓的趋势。

图1 不同压力输气管道泄漏天然气浓度

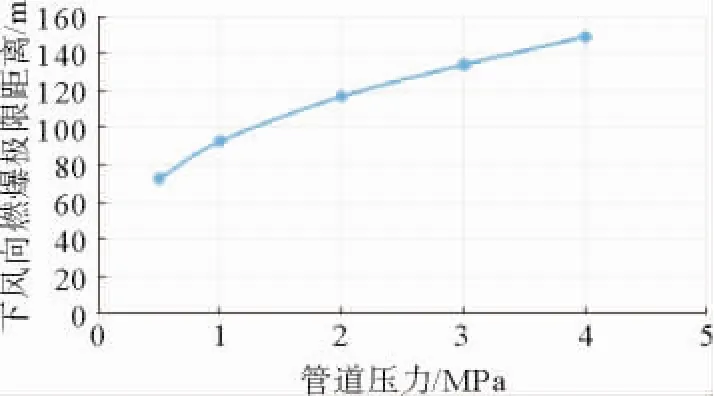
图2 不同压力输气管道泄漏下风向燃爆距离

2.2 泄漏时间影响

图3模拟了默认取值条件下，泄漏天然气浓度随时间的变化，可以看出随着泄漏时间增加，燃爆区域在下风向和垂直于下风向的方向均出现明显扩张。当天然气仅泄漏30 s时，其下风方向的燃爆极限距离已经达到134 m，垂直于下风方向的燃爆距离达到48 m，表明天然气发生泄漏后，潜在危险区域会迅速扩张，且泄漏时间越长，危险区域越大。因此针对天然气泄漏，应及时发现，及时处理，避免危险发生。图4模拟了不同泄漏时间下风向燃爆极限距离，容易看出下风向燃爆极限距离随着时间增加先迅速上升，后逐渐趋于平缓。这是因为天然气开始泄漏速度快，后随着管道压力递减，泄漏速度逐渐减慢，泄漏天然气趋向于扩散，从而导致下风方向燃爆距离增加逐渐变缓。

图3 不同泄漏时间泄漏天然气浓度

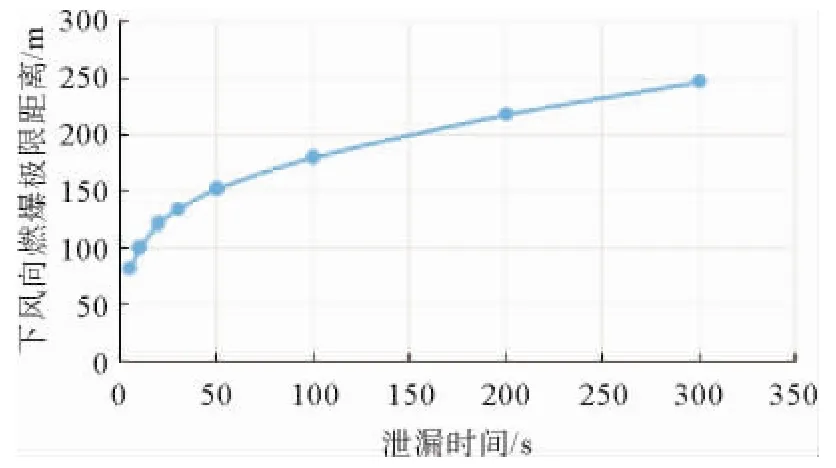
图4 不同泄漏时间下风向燃爆极限距离

2.3 大气稳定度影响

大气稳定度综合了风速、天气与云层等多方面因素，是表征地区环境因素的综合参数。图5模拟了大气稳定度分别为A级、C级与E级时，泄漏天然气的浓度分布图。可以看出，大气稳定度主要影响泄漏天然气在下风向的扩散，A级的燃爆区域最小，E级的燃爆区域最大。图6模拟了不同大气稳定度下下风向的极限燃爆距离，从A级到F级，下风向的极限燃爆距离增加幅度越来越大，表明大气稳定度为D～F级时，天然气沿下风向更容易扩散。结合表2，可以得知，白天由于日照影响，风速较低时，天然气更垂向扩散，致使地面天然气扩散速度慢，燃爆区域小，随着地面风速增加，地面天然气扩散逐渐占据主导，从而形成更长的燃爆区域带;夜晚时，没有日照影响，则情况相反，在风速较低时更容易形成高浓度的稳定扩散云。夜晚没有日照，天然气垂向扩散能力弱，更趋向于地面扩散，因此夜晚天然气泄漏形成燃爆区域白天更大，更危险。

图5 不同大气稳定度泄漏天然气浓度

3 新场气田应用

新场气田某干线是重要管线之一，全长11 km，途径5座井站，运行压力约为1.5 MPa。管线多经过农田、村落，地面粗糙度可取0.5，日常风速平均为4 m/s，属于大气稳定度C～D等级，年平均温度为22℃。基于此，计算获得某干线泄漏下风向燃爆极限距离图版，见图7，对指导某干线制定应急预案、安全演练具有重要意义。

4 结论

a)输气管道压力主要影响泄漏点下风向燃爆区域扩展。随着输气管道压力升高，燃爆区域在泄漏点下风向迅速扩张，在其他方向增长微弱。

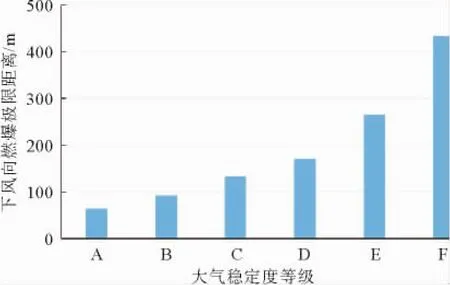
图6 不同大气稳定度下风向极限燃爆距离

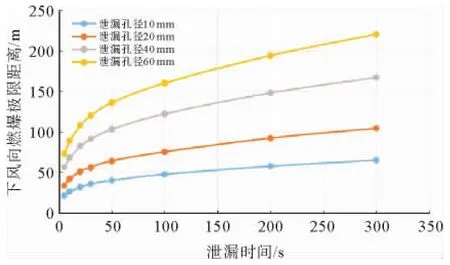
图7 某干线泄漏下风向燃爆极限距离图版

b)泄漏时间是影响泄漏点燃爆区域面积的重要因素。天然气一旦发生泄漏，燃爆区域会迅速增加，泄漏时间越长，危险区域越大。下风向燃爆极限距离随泄漏时间增加而增速逐渐降低。

c)环境因素是影响泄漏天然气燃爆区域大小的重要因素。在白天，由于日照影响，风速越强，燃爆区域越大，在夜晚则不同。相同条件下，天然气在夜晚泄漏形成的燃爆区域大于在白天泄漏时形成的燃爆区域。

d)将模型应用于新场气田某干线，获得了某干线天然气泄漏下风向燃爆极限距离图版，对保障某干线安全生产具有重要意义。