大射电望远镜系统输出滞后补偿方法*
2018-08-02章丹丹尉胜腾
章丹丹,保 宏,尉胜腾,许 谦
(1. 西安电子科技大学电子装备结构教育部重点实验室, 陕西 西安 710071;2. 中国科学院新疆天文台, 新疆 乌鲁木齐 830011)
引 言
大口径、高频段是射电望远镜的发展趋势。然而大口径导致射电望远镜的结构固有频率降低和柔性增加,高频段要求射电望远镜具有更高的指向精度,这势必为大口径高频段射电望远镜伺服指向控制系统的设计和实现带来巨大的挑战。因此,高精度伺服指向控制成为当前射电望远镜的关键技术。
为了满足大口径射电望远镜伺服指向控制系统高精度的要求,先后有众多学者对此进行了研究,并且提出了一系列方法。在口径较小的天线中,传统的比例积分(PI)控制算法就可以取得很好的控制效果[1]。而PI控制器在调节的过程中会出现积分饱和现象,只单纯的调节PI增益会导致系统的高频不确定性,进而使大口径射电望远镜的谐振情况无法估计,从而难以保证其高精度指向要求[2]。为了提高系统响应速度,减小结构谐振对伺服控制性能的影响,有学者将凹口滤波器和PI控制器结合用于伺服系统的设计中。但是由于大射电望远镜的结构柔性增大导致固有频率密集存在着不确定性且在不同仰角下基频会发生变化,在实际工程中凹口滤波器并不能精确抑制大射电望远镜的谐振现象[3]。文献[4]提出了线性二次型高斯(LQG)控制方法,构造高频谐振估计器,有效抑制大射电望远镜的高频谐振。然而LQG控制器是基于数学模型设计的,大口径天线的模型不易推导,故文献[5]提出了基于输入输出的子空间建模方法,但是该方法未反映出系统的物理意义。为了解决由外界扰动以及模型摄动存在导致的系统不稳定问题,文献[6]提出了H∞控制方法,可以保障系统的鲁棒性[7-9],但是其不确定性函数在工程实践中难以获得。大口径射电望远镜的工作环境使得扰动等随机误差成为影响高控制精度的因素,文献[10]将自抗扰控制技术运用于大口径射电望远镜的伺服控制,虽然该技术可以有效的抵抗外界扰动,但是对于射电望远镜结构的柔性却不能处理。上述文献均未考虑到大口径天线的输出滞后问题,滞后的存在使得系统动态性能下降,指向精度降低,容易引起超调和振荡。尤其对于大型柔性结构来说,一旦受到扰动的作用,其振动将会持续很长时间,如不及时抑制,不仅会影响装置的精度,甚至可能导致结构的损坏。
本文针对大口径天线的输出滞后问题,提出了一种输出滞后鲁棒控制器设计方法,该方法的优点是可以在系统不确定性以及扰动的作用下维持自身的稳定性以及动态性能。本文章节内容如下:第1节简要介绍将时间滞后等价成扰动问题,第2节设计输出滞后鲁棒控制器,第3节通过半实物仿真平台实验验证了该方法的可靠性,最后对本文进行了总结。
1 提出问题
大口径天线的第i阶模态的状态空间方程[11]可以表示为
(1)
其中,
(2)
(3)
式中:Ami、Bmi、Cmi分别表示第i阶模态对应的状态矩阵,输入矩阵和输出矩阵,i=1对应的是刚性模态,i=2,3,…,n对应的是柔性模态。由于大口径天线刚性的存在,其大惯量会带来输出滞后问题。输出滞后的存在使得被控量不能及时的反应系统所承受的扰动,这对系统的工作非常不利,尤其是在大口径射电望远镜对指向精度要求较高的情况下。
根据天线模型式(1)可以得出其传递函数,即G(s)=Cmi(sI-Ami)-1Bmi,如果只关注输入和输出滞后,可将具有输出滞后的天线系统简化为如图1所示。
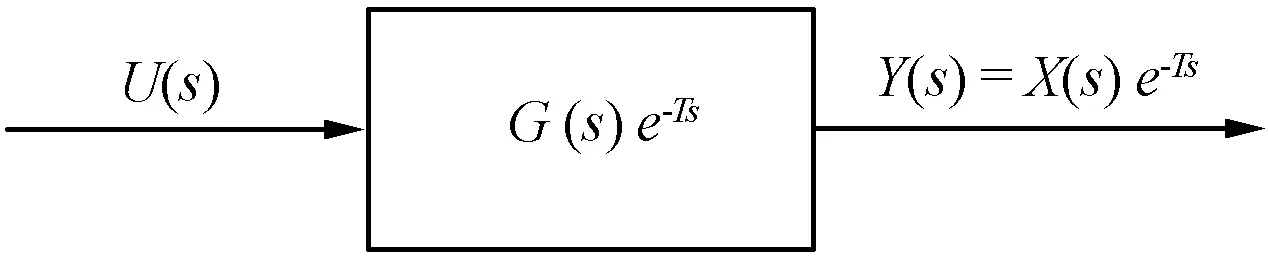
图1 具有输出滞后的天线系统
将输出滞后等效成扰动即Dnet(s):
Dnet(s)=U(s)-U(s)e-Ts
(4)
B(s)=U(s)-[U(s)-U(s)e-Ts]=U(s)e-Ts
(5)
式中:T表示滞后时间。
那么图1可转化为图2所示的系统。

图2 等效成扰动后的系统
此时系统的状态方程和输出方程如式(6)所示:
(6)
式中:A、b、c分别表示系统的状态矩阵、输入矩阵和输出矩阵;x(t)、y(t)分别代表系统的状态向量和输出。
因此,图1所示的系统中输出滞后可以等效为图2中的外部扰动,同时摩擦和间隙也会导致系统输出滞后,使系统的精度降低,动态品质下降。
2 输出滞后鲁棒控制器设计
2.1 确定扰动的边界
通常在进行鲁棒控制器设计时需要知道不确定性边界,在这里采用基于鲁棒阶跃响应辨识方法[13]确定扰动的边界,其基本思想如下:加入阶跃响应信号来引起系统明显的动态响应,然后在系统响应近似进入稳定状态后移除该信号,最后通过采集到的数据进行参数辨识。
已知天线的模型式(1)可以用如下的一般式表示,即:
(7)
考虑到输出滞后时,相应的时域响应为
any(n)(t)+…+a1y(t)+a0y(t)=bmu(m)(t-τ)+
…+b0u(t-τ)+l(t)
(8)
式中:y(t)表示系统输出;u(t)表示系统输入;l(t)表示由于负载干扰而形成的系统输出的偏差;τ表示系统的滞后时间;b0/a0为系统的增益。
对式(8)两边分别进行n+1次积分,然后重新整理得到参数估计的最小二乘式:
Ψ(t)=φT(t)γ+ε(t)
(9)
式中:Ψ(t)表示对y(t)的积分;γ表示估计参数矢量;ε(t)表示残留误差;φ(t)表示对u(t-τ)的积分。通过求解式(9),可以得到式(8)中的所有常数项即b0,b1,…,bm,a0,a1,…,an和τ,从而确定扰动的边界。
2.2 输出滞后鲁棒控制器设计
大射电望远镜伺服控制系统中摩擦、间隙和大惯量造成的滞后对系统影响较大,并且在第一部分中已经把输出滞后部分等效成了扰动。扰动的存在使得系统的输出产生不规律的振动,同时射电望远镜的结构柔性使得其在跟踪过程中产生柔性振动,两种振动叠加在一起对系统的性能造成了损害。考虑扰动和不确定性后,该伺服系统的控制框图可用如图3所示的形式表示,图中r为参考输入;d为扰动输入;yd为控制输出;u为控制器输入;e为控制误差;Pr表示实际系统;Pn为被控系统标称模型;Δs为模型不确定性。
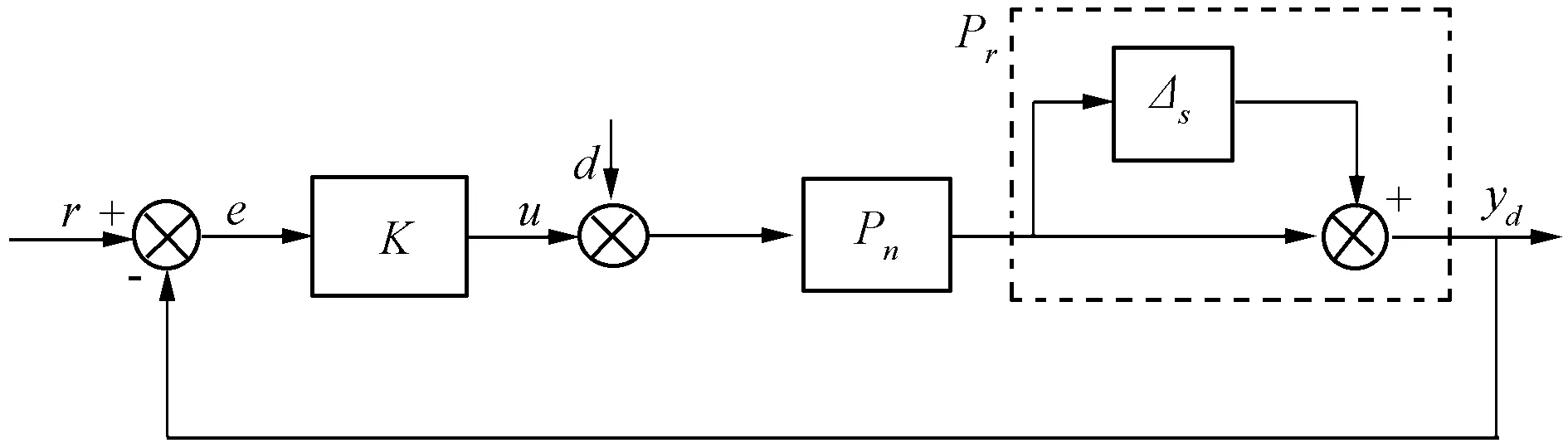
图3 伺服系统控制框图
伺服控制系统的开环频率响应Ln(ω)为
Ln(ω)=Pr(ω)K(ejωτ)
(10)
则系统的灵敏度函数为
(11)
补灵敏度函数为
(12)
在寻找控制器时,应选择一个权重函数Wp(ω)对灵敏度函数进行加权,Wp(ω)的值可以根据式(4)确定。选择权重函数Wu(ω)对补灵敏度函数进行加权,Wu(ω)可表示为

(13)
权重函数Wp和Wu确定后,系统的灵敏度函数和补灵敏度函数也能确定,鲁棒控制器K的传递函数就得到了。把伺服系统与LQG柔性控制器看成一个总的被控系统。在PI+LQG传统控制方法的基础上针对扰动设计输出滞后鲁棒控制器,把这两者相乘结合,可以得到一个理想的鲁棒控制器,如图4所示:K代表鲁棒控制器;r是参考信号;e是误差信号;d是扰动信号;y是负载转角。

图4 鲁棒控制器结构图
3 实验算例
将本文中的方法应用到半实物仿真平台中检验该输出滞后鲁棒控制器的应用效果。实验装置包括主机、IMDU驱动平台、皮带、负载配重(铜块)、功率放大器和Q8板卡。该实验平台可以使用Matlab直接编译,操作简单。控制对象是IMDU系统,主要包括4根轴,2根电机轴和2根负载轴。每根轴在模块内部都装有编码器用来测量轴的转动角度,由线性电流放大器来驱动每个直流电机。首先,把IMDU模块中的一根电机轴与一根负载轴用皮带连接起来;然后,将仪器的输入输出接口与Q8板卡相接,这样仪器、板卡和主机就构成了一个闭环回路,在连接好系统之后,利用Matlab语言和Simulink构建控制框图。接着把控制框图编译成代码并下载到主机相应的目录中;最后,打开所有硬件开关,在Simulink中运行控制框图,在显示器上就能看到物理量的大小和变化情况。最终的实验目标是使系统在扰动和时间滞后存在的条件下依然能快速稳定的跟踪参考信号。
利用阶跃响应辨识方法,对两惯量半实物系统进行辨识,其中负载轴上安装了4个铜块作为负载。给系统施加一定的电压与滞后时间,采集负载轴的角速度信号,然后对其进行程序运算处理,辨识得到系统速度环传递函数,进而求得各个参数。
从力矩到负载轴角速度的传递函数为
G(s)=
(14)
式中:B1表示电机粘性阻尼;B2表示负载粘性阻尼;J1表示电机的转动惯量;J2表示负载的转动惯量;Ks表示扭转刚度;τ表示滞后时间。
具体实验步骤为:先施加给系统6.285 A的电流,此时电机的输出力矩为0.39 N·m,待负载轴转速稳定后,增大电流至7.854 A,此时电机的输出力矩为0.48 N·m,开始采集负载轴角速度数据,当负载轴角速度再次趋于稳定时,减少电流至6.285 A,继续采集数据至转速稳定。最终对采集得到的数据进行处理,得到辨识结果为
(15)
联立式(14)和式(15),得到B1、B2、Ks、J1、J2和τ,与理论值对比见表1。
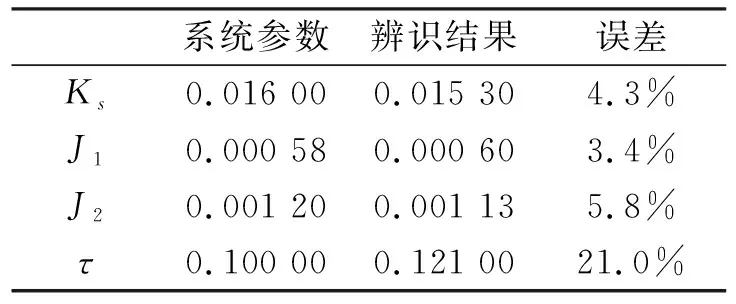
表1 辨识结果对比
根据式(4),性能权重函数取为
(16)
不确定性权重函数Wu(ω)按照参数辨识的误差及经验,取为
(17)
鲁棒控制器传递函数为
(18)
实验分为4种情况:1)无滞后系统,采用图4所示的传统控制方法;2)含滞后系统仍采用传统控制方法,其中滞后时间τ=0.1 s;3)无滞后系统,采用图4所示本文提出的控制方法;4)含滞后时间系统,采用本文提出的控制方法,滞后时间τ=0.1 s。将这4种情况的实验结果进行对比。实验框图如图5所示。
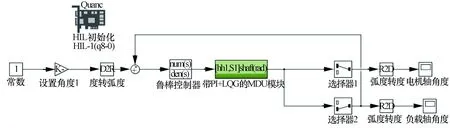
图5 实验框图
系统参考信号为25°阶跃信号,实验得到的对比图如图6所示。

图6 4种情况对比图
由图6可知:无滞后系统,采用如图4所示的传统控制方法,系统在1.2 s 时到达稳定;含滞后系统,仍采用传统控制方法,此时系统出现了明显的超调量和连续的振荡,其中最大振荡时超调量为52%,需要较长时间才能到达稳定状态,控制效果较差;采用本文的控制方法后,在无滞后系统和含滞后系统中,系统到达稳态的时间为3 s,与无滞后系统采用传统方法相比时间变长,但相比于有滞后系统采用传统控制方法来说,超调量显著下降40%,且在3 s时就稳定。
从实验结果对比图可知:加入鲁棒控制器后,含滞后系统的性能得到了明显的改善和提高,充分发挥了鲁棒控制器可以减少外界扰动对系统的影响,保证一定指向精度的作用。
4 结束语
本文针对大口径射电望远镜存在的输出滞后问题,提出了一种新的基于鲁棒控制的方法。通过大量的仿真并在IMDU两惯量系统上进行了实验,得到了如下结论:
1)本文提出的方法可以有效地抵抗扰动;
2)仅在传统控制方法的基础上加上一个鲁棒控制器,操作简单,易于实现,针对同一实验模型采用2种控制方法进行对比,发现加入输出滞后鲁棒控制器后,系统的性能得到了提高和明显的改善;
3)本文中滞后时间是定值,尚未考虑到其在一定范围内变化时的情况,后续将会在这一方面继续研究。
